机器学习——决策树和随机森林
目录
- 熵
-
- 信息熵
- 条件熵
- 相对熵(KL散度)
- 交叉熵
- 决策树
-
- ID3 信息增益
- C4.5 信息增益率
- CART树 基尼指数
- 剪枝——过拟合处理
- 随机森林
-
- Bagging策略
- 随机森林
- 样本不均衡的常用处理方法
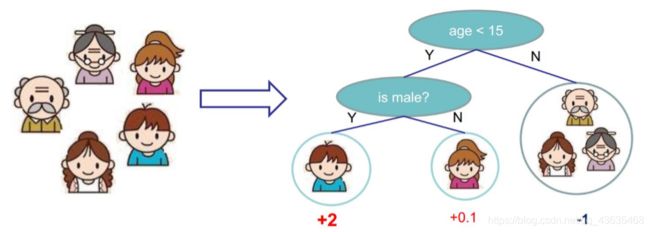
决策树(decision tree)是一种基本的分类与回归方法,决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布,其主要优点是模型具有可读性,分类速度快。决策树学习通常包括三个步骤:特征选择,决策树的生成和决策树的修剪。而随机森林则是由多个决策树所构成的一种分类器,更准确的说,随机森林是由多个弱分类器组合形成的强分类器。
熵
熵 (entropy) 这一词最初来源于热力学。1948年,克劳德·爱尔伍德·香农将热力学中的熵引入信息论,所以也被称为香农熵 (Shannon entropy),信息熵 (information entropy)。
信息熵
信息是一个很抽象的概念,泛指人类社会传播的一切内容。引入“信息熵”概念是为了将信息量化。一条信息的信息量大小和它的不确定性有直接的关系,若要弄清楚一件非常不确定的事,就需要了解大量的信息。相反,若对某件事已经有了较多的了解,那么就不需要太多的信息就能把它搞清楚。所以,从这个角度我们可以认为,信息量的度量就等于不确定性的多少。

H ( X ) H(X) H(X)就被称为随机变量 x x x的熵,它是表示随机变量不确定的度量,是对所有可能发生的事件产生的信息量的期望。
随机变量的取值个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。当随机分布为均匀分布时,熵最大。
将一维随机变量分布推广到多维随机变量分布,则其联合熵 (Joint entropy) 为:
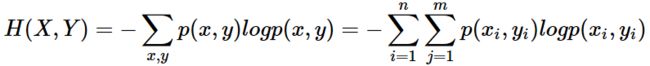
1、熵只依赖于随机变量的分布,与随机变量取值无关,所以也可以将 X X X的熵记作 H ( p ) H(p) H(p)。
2、令0log0=0(因为某个取值概率可能为0)。
条件熵
条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X)表示在已知随机变量 X X X的条件下,随机变量 Y Y Y的不确定性。
H ( Y ∣ X ) H(Y|X) H(Y∣X)定义为 X X X给定条件下 Y Y Y的条件概率分布的熵对 X X X的数学期望:
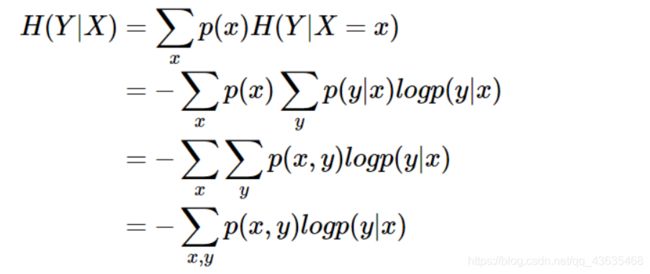
条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X)相当于联合熵 H ( X , Y ) H(X,Y) H(X,Y)减去单独的熵 H ( X ) H(X) H(X),即 H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H(Y|X)=H(X,Y)-H(X) H(Y∣X)=H(X,Y)−H(X)
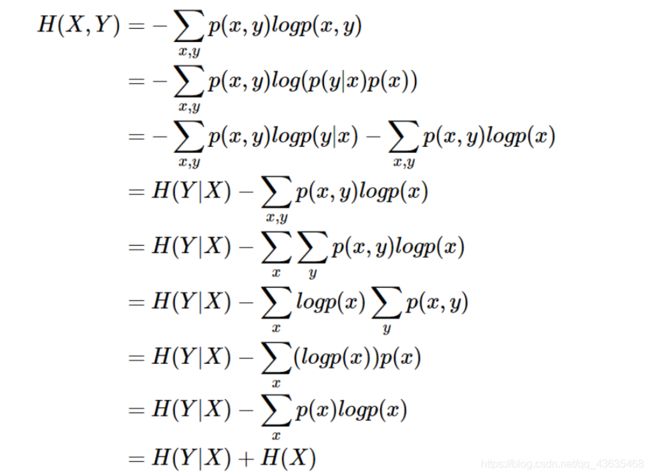
描述 X X X和 Y Y Y所需的信息是描述 X X X自己所需的信息,加上给定 X X X的条件下具体化 Y Y Y所需的额外信息。

相对熵(KL散度)
设 p ( x ) 、 q ( x ) p(x)、q(x) p(x)、q(x)是离散随机变量 X X X中取值的两个概率分布,则 p p p对 q q q的相对熵是:

性质:
1、
如果 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)两个分布相同,那么相对熵等于0;
2、
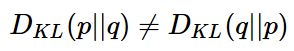
3、
![]()
相对熵可以用来衡量两个概率分布之间的差异,上面公式的意义就是求 p p p与 q q q之间的对数差在 p p p上的期望值。
交叉熵
现在有关于样本集的两个概率分布 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x),其中 p ( x ) p(x) p(x)为真实分布, q ( x ) q(x) q(x)为非真实分布。如果用一个样本的分布 p ( x ) p(x) p(x)来衡量整体预测分布:
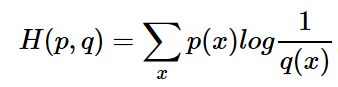
当 H ( p ) H(p) H(p)为常量时(在机器学习中,训练数据分布是固定的),最小化相对熵 D ( p ∣ ∣ q ) D(p||q) D(p∣∣q)等价于最小化交叉熵 H ( p , q ) H(p,q) H(p,q)也等价于最大化似然估计。交叉熵可以用来计算学习模型分布与训练分布之间的差异,交叉熵广泛用于逻辑回归的Sigmoid和Softmax函数中作为损失函数使用。
决策树
决策树分类从根节点开始,对实例的某一特征进行测试,根据测试结果将实例分配到其子节点。每一个子节点对应着该特征的一个取值。如此递归地对实例进行测试并分配,直至达到叶节点,最后将实例分配到叶节点的类中。
决策树学习的算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行划分。如果利用一个特征进行分类的结果与随机分类的结果没有很大差别,则称这个特征是没有分类能力的。通常特征选择的准则是信息增益或信息增益比,特征选择的常用算法有ID3,C4.5,CART。
ID3 信息增益
当熵和条件熵中的概率由数据估计(特别是,极大似然估计)得到时,所对应的熵和条件熵分别称为经验熵和经验条件熵。
信息增益表示得知特征A的信息而使得类X的信息的不确定性减少的程度。
特征 A A A对训练数据集D的信息增益 g ( D , A ) g(D,A) g(D,A):定义为集合 D D D的经验熵 H ( D ) H(D) H(D)与特征 A A A给定条件下 D D D的经验条件熵 H ( D ∣ A ) H(D|A) H(D∣A)之差,即:
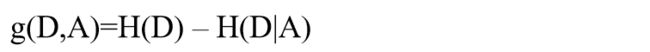
遍历所有特征,对于特征 A A A:
1、计算特征 A A A对数据集 D D D的经验条件熵 H ( D ∣ A ) H(D|A) H(D∣A);
2、计算特征 A A A的信息增益: g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A);
3、选择信息增益最大的特征作为当前的分裂特征。
C4.5 信息增益率
为了避免ID3算法偏向于选择可取值数目较多的属性,定义了信息增益率。信息增益值的大小是相对于训练数据集而言的,并没有绝对意义。在分类为题困难时,也就是说在训练数据集的经验熵大的时候,信息增益值会偏大。反之,信息增益值会偏小。因此,使用信息增益比可以对这一问题进行校正,这是另一种特征选择算法,也即C4.5算法。
定义:特征 A A A对训练数据集 D D D的信息增益比 g r ( D , A ) g_r(D, A) gr(D,A)定义为其信息增益 g ( D , A ) g(D, A) g(D,A)与训练集 D D D的经验熵之比:
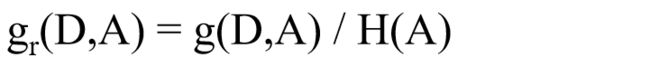
CART树 基尼指数
ID3和C4.5都使用了大量的对数运算,计算量大。CART树是二叉树,因此每次选择最优属性后,再选择该属性的一个取值进行划分。用基尼指数选择最优特征,同时决定该特征的最优二值切分点。
定义:假设有K个类,样本点属于第k类的概率为 p k p_k pk,则概率分布的基尼指数如下
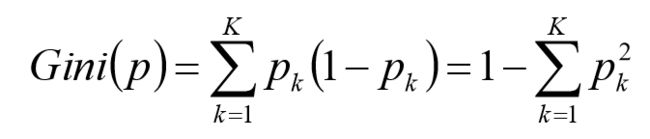
对于给定的样本集合D,其基尼指数为:
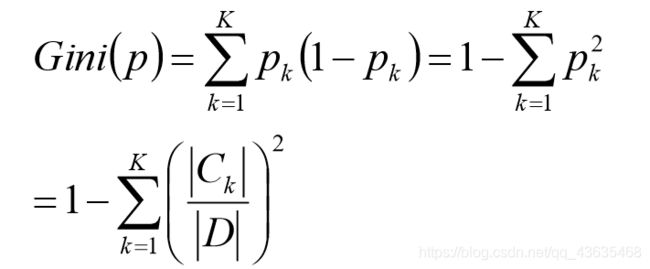
一个特征的信息增益/基尼系数越大,表明特征对样本的熵减少的能力更强,这个特征使得数据由不确定性变成确定性的能力越强。
剪枝——过拟合处理
决策树对训练属于有很好的分类能力,但对未知的测试数据未必有好的分类能力,泛化能力弱。这种过度学习从而精确反映Training Data特征,失去一般代表性而无法应用于新数据分类预测的现象,叫过拟合或过度学习。
剪枝是处理决策树过拟合的常用方法,常用的修剪技术有预剪枝和后剪枝。
预剪枝:
1、构造决策树的过程中,先对每个结点在划分前进行估计,如果当前结点的划分不能带来决策树模型泛化性能的提升,则不对当前结点进行划分并且将当前结点标记为叶结点。
2、事先先指定决策树的最大深度,或最小样本量,以防止决策树过度生长。前提是用户对变量聚会有较为清晰的把握,且要反复尝试调整,否则无法给出一个合理值。决策树生长过深无法预测新数据,生长过浅亦无法预测新数据。
对比未剪枝的决策树和经过预剪枝的决策树可以看出:预剪枝使得决策树的很多分支都没有“展开”,这不仅降低了过拟合的风险,还显著减少了决策树的训练时间开销和测试时间开销。但是,另一方面,预剪枝决策树有可能带来欠拟合的风险。
后剪枝:
后剪枝就是先把整颗决策树构造完毕,然后自底向上的对非叶结点进行考察,若将该结点对应的子树换为叶结点能够带来泛化性能的提升,则把该子树替换为叶结点。
对比预剪枝和后剪枝,能够发现,后剪枝决策树通常比预剪枝决策树保留了更多的分支,一般情形下,后剪枝决策树的欠拟合风险小,泛化性能往往也要优于预剪枝决策树。但后剪枝过程是在构建完全决策树之后进行的,并且要自底向上的对树中的所有非叶结点进行逐一考察,因此其训练时间开销要比未剪枝决策树和预剪枝决策树都大得多。
随机森林
尽管有剪枝等等方法,一棵树的生成肯定还是不如多棵树,因此就有了随机森林,解决决策树泛化能力弱的缺点。
Bagging策略
同一批数据,用同样的算法只能产生一棵树,这时Bagging策略可以帮助我们产生不同的数据集。Bagging策略来源于bootstrap aggregation:从样本集(假设样本集N个数据点)中重采样选出Nb个样本(有放回的采样,样本数据点个数仍然不变为N),在所有样本上,对这n个样本建立分类器(ID3\C4.5\CART\SVM\LOGISTIC),重复以上两步m次,获得m个分类器,最后根据这m个分类器的投票结果,决定数据属于哪一类。
OOB数据
可以发现,Bootstrap每次约有36.79%的样本不会出现在Bootstrap所采集的样本集合中,将未参与模型训练的数据称为袋外数据OOB(Out Of Bag),它可以用于取代测试集用于误差估计。
随机森林
随机森林在bagging的基础上更进一步:
- 样本的随机:从样本集中用Bootstrap随机选取n个样本;
- 特征的随机:从所有属性中随机选取K个属性,选择最佳分割属性作为节点建立CART决策树(泛化的理解,这里面也可以是其他类型的分类器,比如SVM、Logistics);
- 重复以上两步m次,即建立了m棵CART决策树;
- 这m个CART形成随机森林,通过投票表决结果,决定数据属于哪一类(投票机制有一票否决制、少数服从多数、加权多数)。
随机森林算法的注意点:
- 在构建决策树的过程中是不需要剪枝的;
- 整个森林的树的数量和每棵树的特征需要人为进行设定;
- 构建决策树的时候分裂节点的选择是依据最小基尼系数的。
样本不均衡的常用处理方法
假定样本数目A类比B类多,且验证不平衡。
一、A类欠采样(效果较好)
- 随机欠采样;
- A类分割成若干子类,分别于B类进入ML模型;
- 基于聚类的A类分割。
二、B类过采样
避免欠采样造成的信息丢失,相比于欠采样,过采样计算量较大,且会将B类样本的噪声放大。
三、B类数据合成
随机插值得到新样本(SMOTE)。
四、代价敏感学习
降低A类权值,提高B类权值