机器学习——模型评估、选择与验证

训练集与测试集

为了使机器学习训练的模型有效，可以用于实际情况中，我们不仅需要用训练集来对模型进行训练，还需要用测试集对模型进行测试以验证其可靠高效性。即训练集用来构建机器学习模型，测试集用来评估模型性能。
通常情况下我们都是将数据分为百分之八十和百分之二十，多的那部分用来做训练集，少的那部分用来做测试集。

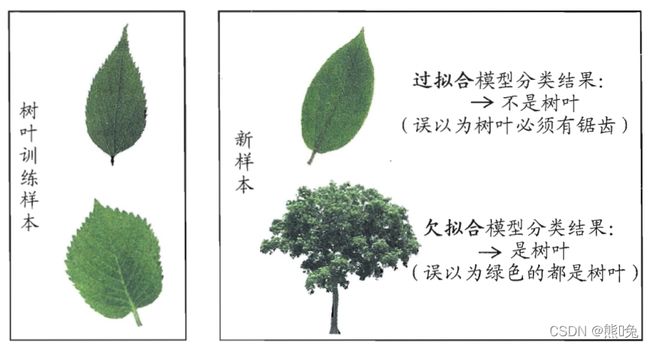
过（欠）拟合

① 欠拟合：模型在训练集上误差很高；
原因：模型过于简单，没有很好的捕捉到数据特征，不能很好的拟合数据。

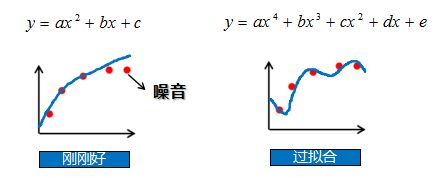
② 过拟合：在训练集上误差低，测试集上误差高；
原因：模型把数据学习的太彻底，以至于把噪声数据的特征也学习到了，这样就会导致在后期测试的时候不能够很好地识别数据，模型泛化能力太差。

在分类问题中的实例说明：

偏差与方差

偏差：预计值的期望与真实值之间的差距；
方差：预测值的离散程度，也就是离其期望值的距离；
我们知道欠拟合是模型在训练集上误差过高，过拟合模型是在训练集上误差低，在测试集误差高，那么模型误差的来源是什么呢？其实，模型在训练集上的误差来源主要是偏差，在测试集上误差来源主要是方差。

欠拟合是一种高偏差的情况，过拟合是一种低偏差，高方差的情况。

验证集与交叉验证

在机器学习中，通常需要评估若⼲候选模型的表现并从中选择模型。这⼀过程称为模型选择。可供选择的候选模型可以是有着不同超参数的同类模型。以神经网络为例，我们可以选择隐藏层的个数，学习率大小和激活函数。为了得到有效的模型，我们通常要在模型选择上下⼀番功夫。从严格意义上讲，测试集只能在所有超参数和模型参数选定后使⽤⼀次。不可以使⽤测试数据选择模型，如调参。由于⽆法从训练误差估计泛化误差，因此也不应只依赖训练数据选择模型。鉴于此，我们可以预留⼀部分在训练数据集和测试数据集以外的数据来进⾏模型选择。这部分数据被称为验证数据集，简称验证集。
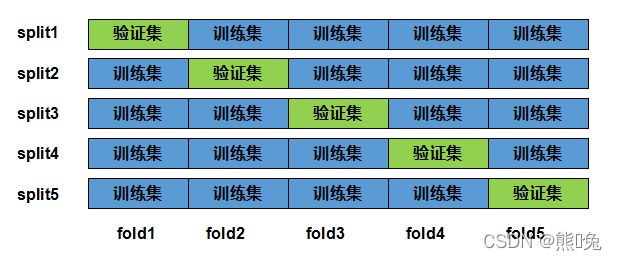
k折交叉验证
由于验证数据集不参与模型训练，当训练数据不够⽤时，预留⼤量的验证数据显得太奢侈。⼀种改善的⽅法是 K 折交叉验证。在 K 折交叉验证中，我们把原始训练数据集分割成 K 个不重合的⼦数据集，然后我们做K次模型训练和验证。每⼀次，我们使⽤⼀个⼦数据集验证模型，并使⽤其它 K−1 个⼦数据集来训练模型。在这 K 次训练和验证中，每次⽤来验证模型的⼦数据集都不同。最后，我们对这 K 次训练误差和验证误差分别求平均。（根据所有子模型评分的平均值来选择超参数）

集成学习
在机器学习的有监督学习算法中，我们的目标是学习出一个稳定的且在各个方面表现都较好的模型，但实际情况往往不这么理想，有时我们只能得到多个有偏好的模型（弱监督模型，在某些方面表现的比较好）。集成学习就是组合这里的多个弱监督模型以期得到一个更好更全面的强监督模型。集成学习潜在的思想是即便某一个弱分类器得到了错误的预测，其他的弱分类器也可以将错误纠正回来。集成方法是将几种机器学习技术组合成一个预测模型的元算法，以达到减小方差、偏差或改进预测的效果。

自助法
在统计学中，自助法是一种从给定训练集中有放回的均匀抽样，也就是说，每当选中一个样本，它等可能地被再次选中并被再次添加到训练集中。自助法以自助采样法为基础，给定包含 m 个样本的数据集 D，我们对它进行采样产生数据集 D’；每次随机从 D 中挑选一个赝本，将其拷贝放入 D’，然后再将该样本放回初始数据集 D 中，使得该样本在下次采样时仍有可能被采到；这个过程重复执行 m 次后，就得到了包含m个样本的数据集 D’，这就是自助采样的结果。自助法在数据集较小、难以有效划分训练/测试集时很有用；此外，自助法能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处。然而，自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差。

衡量回归的性能指标

对于分类问题，可以使用正确率来评估模型的性能；那回归问题用什么指标来进行评估呢？
简单来说吧，可以使用均方误差（MSE），均方根误差（RMSE），平均绝对误差（MAE），R-Squared。（这里我们前面的博客中有具体介绍）

准确度的陷阱与混淆矩阵

准确率的缺陷
准确率就是正确率，

预测值	真实值
1	1
2	1
0	1
0	0
2	3

现在让你算一下它的准确度，不用思考吧，它就是五分之二。那现在可能会认为准确度越高模型分类性能越好，实际上不一定。
假如现在有一个人本身已经患有癌症，但是他自己不知道自己患有癌症。这个时候用我的癌症检测系统（系统准确率高达99%）检测发现他没有得癌症，那很显然我这个系统已经把他给害了。看到这里您应该已经体会到了，一个分类模型如果光看准确度是不够的，尤其是对这种样本极度不平衡的情况（ 10000 条健康信息数据中，只有 1 条的类别是患有癌症，其他的类别都是健康）。
混淆矩阵
想进一步的考量分类模型的性能如何，可以使用其他的一些性能指标，例如精准率和召回率，但这些指标计算的基础是混淆矩阵。
来看看例子，增强一下理解：癌症检测系统的输出不是有癌症就是健康，这里用1 表示有癌症，0表示健康。假设现在有10000条数据来进行测试，其中有9978条数据的真实类别是0，系统预测的类别也是0；有2条数据的真实类别是1却预测成了0；有12 条数据的真实类别是0但预测成了1；有8条数据的真实类别是1，预测结果也是1。
现在将数据组成以下矩阵，该矩阵就是混淆矩阵


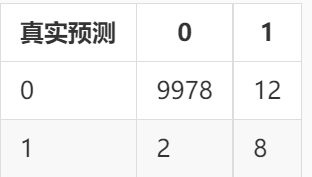
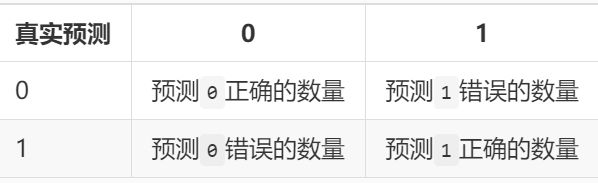
现在将正确看成True，错误看成False，0看成Negtive，1看成Positive，混淆矩阵如下：

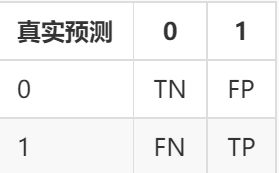
因此 TN 表示真实类别是 Negtive，预测结果也是 Negtive 的数量； FP 表示真实类别是 Negtive，预测结果是 Positive 的数量； FN 表示真实类别是 Positive，预测结果是 Negtive 的数量；TP 表示真实类别是 Positive，预测结果也是 Positive 的数量。当 FN 和 FP 都等于 0 时，模型的性能应该是最好的，因为模型并没有在预测的时候犯错误。

def confusion_matrix(y_true, y_predict):  
    def TN(y_true, y_predict):  
        return np.sum((y_true == 0) & (y_predict == 0))
    def FP(y_true, y_predict):  
        return np.sum((y_true == 0) & (y_predict == 1))
    def FN(y_true, y_predict):  
        return np.sum((y_true == 1) & (y_predict == 0))
    def TP(y_true, y_predict):  
        return np.sum((y_true == 1) & (y_predict == 1))
    return np.array([  
        [TN(y_true, y_predict), FP(y_true, y_predict)],  
        [FN(y_true, y_predict), TP(y_true, y_predict)]  
    ])

精准率和召回率

精准率（precision） 模型预测为 Positive 时的预测准确度

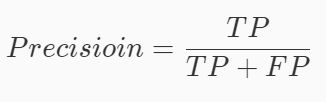
假设上面说到的癌症检测系统的例子，系统的准确率为
8/(8+12)=0.4，0.4值表示癌症检测系统的预测结果中如果有100个人被预测成有癌症，那么其中有40个人是真的有癌症。由此可看出，精准率越高那系统预测某人有癌症的可信度就越高。
**召回率（recall）**我们关注的事件发生了，并且模型预测正确了的比值。

同样上面系统的召回率 =8/(8+2)=0.8。从计算出的召回率可以看出，假设有 100 个患有癌症的病人使用这个系统进行癌症检测，系统能够检测出 80 人是患有癌症的。也就是说，召回率越高，那么我们感兴趣的对象成为漏网之鱼的可能性越低。
那是不是精确率，召回率越高越好呢？
不一定哦，有时候得根据具体情况来进行判断分析，有时候模型的精确率变高，召回率会变低，而有时候精确率变低，召回率会变高。但是再来看看具体的例子：
① 比如我现在想要训练一个模型来预测我关心的股票是涨( Positive )还是跌( Negtive )，那么我们应该主要使用精准率作为性能指标。因为精准率高的话，则模型预测该股票要涨的可信度就高。
② 比如现在需要训练一个模型来预测人是( Positive )否( Negtive )患有艾滋病，那么我们应该主要使用召回率作为性能指标。因为召回率太低的话，很有可能存在漏网之鱼（可能一个人本身患有艾滋病，但预测成了健康），这样就很可能导致病人错过了最佳的治疗时间，这是非常致命的。

import numpy as np

def precision_score(y_true, y_predict):
    def TP(y_true, y_predict):  
        return np.sum((y_true == 1) & (y_predict == 1))
    def FP(y_true, y_predict):  
        return np.sum((y_true == 0) & (y_predict == 1))
    tp = TP(y_true, y_predict)  
    fp = FP(y_true, y_predict)  
    try:  
        return tp / (tp + fp)  
    except:  
        return 0.0  
   

def recall_score(y_true, y_predict):
    def FN(y_true, y_predict):  
        return np.sum((y_true == 1) & (y_predict == 0))
    def TP(y_true, y_predict):  
        return np.sum((y_true == 1) & (y_predict == 1))
    tp = TP(y_true, y_predict)  
    fn = FN(y_true, y_predict)  
    try:  
        return tp / (tp + fn)  
    except:  
        return 0.0  

F1 Score

前面有说到，精准率变高，召回率会变低，精准率变低，召回率会变高。那如果想要同时兼顾精准率和召回率，就需要用到F1 Score来作为性能度量指标啦。同时兼顾了分类模型的准确率和召回率。 F1 Score 可以看作是模型准确率和召回率的一种加权平均，它的最大值是 1，最小值是 0。

ROC AUC

ROC曲线 ( Receiver Operating Cha\fracteristic Curve )描述的 TPR （ True Positive Rate ）与 FPR （ False Positive Rate ）之间关系的曲线。

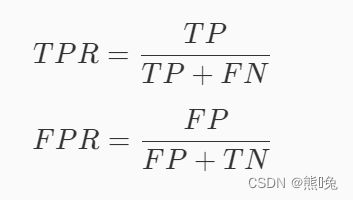
好吧，这里的TPR 就是召回率。所以 TPR 描述的是模型预测 Positive 并且预测正确的数量占真实类别为 Positive 样本的比例。而 FPR 描述的模型预测 Positive 并且预测错了的数量占真实类别为 Negtive 样本的比例。
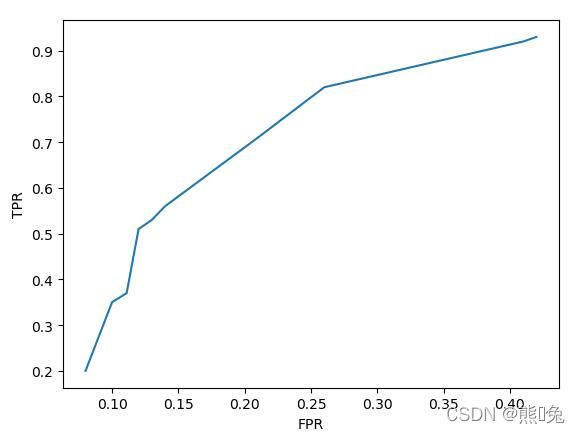
当模型的 TPR 越高 FPR 也会越高， TPR 越低 FPR 也会越低。这与精准率和召回率之间的关系刚好相反。若将 FPR 作为横轴， TPR 作为纵轴，将上面的表格以折线图的形式画出来就是 ROC曲线 。

假设现在有模型 A 和模型 B ，它们的 ROC 曲线如下图所示(其中模型 A 的 ROC曲线 为黄色，模型 B 的 ROC 曲线 为蓝色)：

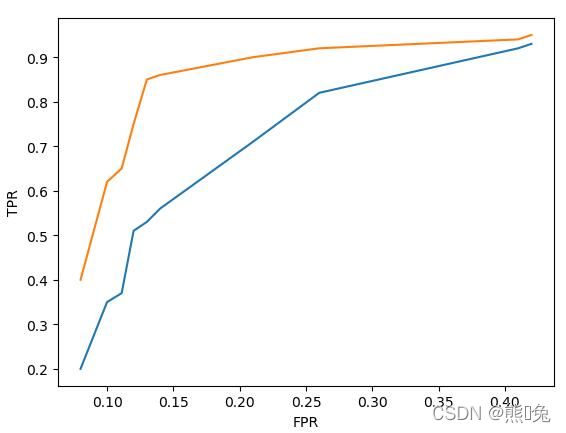
那么模型 A 的性能比模型 B 的性能好，因为模型 A 当 FPR 较低时所对应的 TPR 比模型 B 的低 FPR 所对应的 TPR 更高。由由于随着 FPR 的增大， TPR 也会增大。所以 ROC 曲线与横轴所围成的面积越大，模型的分类性能就越高。而 ROC曲线 的面积称为AUC。
很明显模型的 AUC 越高，模型的二分类性能就越强。

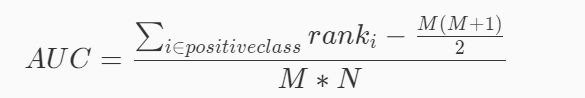
其中 M 为真实类别为 Positive 的样本数量，N 为真实类别为 Negtive 的样本数量。ranki 代表了真实类别为 Positive 的样本点额预测概率从小到大排序后，该预测概率排在第几。

import numpy as np

def calAUC(prob, labels):
    '''
    计算AUC并返回
    :param prob: 模型预测样本为Positive的概率列表，类型为ndarray
    :param labels: 样本的真实类别列表，其中1表示Positive，0表示Negtive，类型为ndarray
    :return: AUC，类型为float
    '''
    f = list(zip(prob, labels))  
    # 按概率从小到大排序  
    rank = [values2 for values1, values2 in sorted(f, key=lambda x:x[0])]  
    # 得到rank  
    rankList = [i+1 for i in range(len(rank)) if rank[i] == 1]
    posNum = 0  
    negNum = 0  
    for i in range(len(labels)):  
        if(labels[i] == 1):  
            posNum += 1  
        else:  
            negNum += 1
    # 根据公式计算AUC  
    auc = (sum(rankList) - (posNum*(posNum+1))/2)/(posNum*negNum)  
    return auc  

sklearn中的分类性能指标（接口）

accu\fracy_score

sklearn 提供了计算准确度的接口 accu\fracy_score
·y_true：为样本真实标签，类型为一维的 ndarray 或者 list。
·y_pred：为模型预测标签，类型为一维的 ndarray 或者 list。

from sklearn.metrics import accu\fracy_score  

precision_score

sklearn 提供了计算精准率的接口 precision_score 。其中参数如下：

·y_true：为样本真实标签，类型为一维的 ndarray 或者 list；
·y_pred：为模型预测标签，类型为一维的 ndarray 或者 list；
·pos_label：用什么值表示 Positive，默认为 1。

from sklearn.metrics import precision_score  

recall_score

sklearn 提供了计算召回率的接口 recall_score 。其中参数如下：
·y_true：为样本真实标签，类型为一维的 ndarray 或者 list。
·y_pred：为模型预测标签，类型为一维的 ndarray 或者 list。
·pos_label：用什么值表示 Positive ，默认为 1。

from sklearn.metrics import recall_score  

f1_score

sklearn 提供了计算 F1 Score 的接口 f1_score 。其中参数如下：

·y_true：为样本真实标签，类型为一维的 ndarray 或者 list。
·y_pred：为模型预测标签，类型为一维的 ndarray 或者 list。
·pos_label：用什么值表示 Positive ，默认为 1。

from sklearn.metrics import f1_score

roc_auc_score

sklearn 提供了计算 AUC 的接口 roc_auc_score 。其中参数如下：

·y_true：为样本真实标签，类型为一维的 ndarray 或者 list；
·y_score：为模型预测样本为 Positive 的概率，类型为一维的 ndarray 或者 list。

from sklearn.metrics import roc_auc_score

来源：头歌