【论文笔记】用于几何匹配的卷积神经网络结构(CNN for Geometric Matching)
用于几何匹配的卷积神经网络结构(CNN for Geometric Matching)
文章目录
- Abstract
- CNN
- Related Work
- Architecture for Geometric Matching
-
- 特征提取：
- Matching Network
- correlation-layer
- 归一化：
- Regression Network
- Geometric Transformations
-
- Affine Transformation
- Homography Transformation（单应性变换）
- Thin-Plate Spline Transformation
- Hierarchy of Transformations
- Iterative Refinement（迭代细化）
- Loss Function（损失函数）
Abstract
本文主要做了两件事:
1.用深度学习方法模拟经典的图像相似度估计问题
2.用深度学习方法估计仿射变换参数，以及更为复杂的thin-plate spline transformation，这样可以提高泛化能力。
CNN
handle large changes of appearance between the matched images
经典的相似度估计方法，比如使用SIFT获取局部特征丢弃不正确的匹配进行模糊匹配，然后将模糊匹配的结果输入到RANSAC或者Hough transform中进行精确匹配，虽然效果不错但是无法应对场景变换较大以及复杂的几何形变的情况。本文使用CNN提取特征以应对这两点不足。
1.用CNN特征替换原有经典特征，即使场景变换很大，也能够很好的提取特征；
2.设计一个匹配和变换估计层，加强模型鲁棒性，提升泛化能力，且不用人工标注数据。
Related Work
其他模型与我们模型的不同：
- 他们需要类标签
- 没有使用CNN的特征
- 他们联合对齐一大堆图片，我们只需要图片对。
- 他们呢没有使用CNN对齐方法
Architecture for Geometric Matching
经典的方法分为三步。
我们的结构:
end-to-end
输入：两幅图片
输出：仿射变换的6个参数
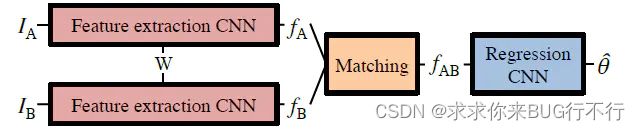
这里的思路如下：先用双路CNN提取两幅图片的特征，然后用correlation-layer进行融合，这个过程可以视为模糊匹配，然后进入回归层得到具体预测出的仿射变换的6个参数。
特征提取：
使用双路CNN，输入两幅图像，权值共享。
CNN采用VGG-16，L2-norm，fine-tuning ImageNet。
Matching Network
我们通过双路CNN获取两幅图片的feature map：
w，h，d：分别为feature map的长、宽、深度（通道）
在进入matching阶段前，要把两路CNN提取到的特征融合为一个向量，这里使用的方法是correlation-layer。
correlation-layer
计算公式：
fA与fB进行点乘得到correlation map (Cab)
原来两个w×h的feature map ，每个1×1×d的向量通过点乘得到w×h×（w×h）这样一个立方体。立方体当中的每一个位置（i，j）表示fB中的（i，j）位置的点对应fA中所有点的相似度。这里correlation map的深度（w×h）即fA中所有点被展开成k，表示fA中点的索引。
归一化：
得到correlation map 后对相似度进行归一化，以凸显相似度高的点。我们使用ReLU+L2Norm进行归一化。为什么选用ReLU呢？考虑这两种情况：
假设只有一个匹配点时，会直接将匹配值增大为1。
假设有多个噪声匹配点，使用ReLU会对除了最匹配的点之外的噪声点降权，提高了模型的鲁棒性。
对correlation map归一化后，我们得到了在进入回归层之前所需要的correspondence map。
使用correlation-layer的原因如下：
两幅图像的相似度只需要保留其相似性以及空间位置，图像本身的特征不应该被考虑。
假设有两对图像的仿射变换参数相同，只是图像内容不同，如果考虑feature map的像素信息，那么两幅图像进入模型后输出的参数也将不同；
如果只是简单的对两幅图中每一个通道的feature进行相加或者相减，如果匹配点相差很远，这种方法无法获取正确的相似度。如果使用correlation map+Norm，即使匹配点相差很远，也能够凸显出最为匹配的点。所以前者方法无法应对场景大范围变化的匹配问题；
Regression Network
这里要注意的是，进入回归层中要使用卷积层而不是全连接层。因为correlation map的参数个数是feature map大小的平方，直接用全连接参数过多将会造成梯度爆炸。
Geometric Transformations
我们使用了三种几何变换参数：affine, homography and thin-plate spline.
Affine Transformation
affine transformation 是使用六自由度线性变换的，参数如下：
B点和A点的对应关系如下：
Homography Transformation（单应性变换）
此变换是将一个四边形改变为其他任意一个四边形，并且还保持着共线性。他有八个自由度，更加复杂。
这些参数可以转换为H矩阵，然后使用下面公式进行改变。
Thin-Plate Spline Transformation
此方法是一个参数化的平滑的2D插值方法。通过分别给定两个图像的K个控制点。本文我们使用K=9，并且将其变为3x3。因为控制点B是所有图片固定的，因此此模型只被控制点A进行参数化。
如下图所解释：
然后A和B的对应关系如下：
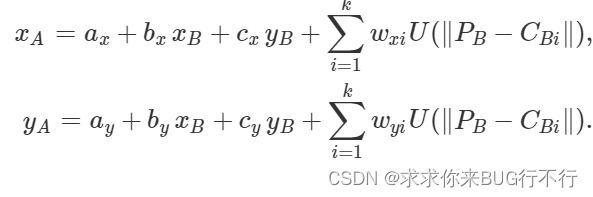
下面给出来U的公式，并且参数a b c w 都是计算出来的，
L−1只需要计算一次即可。
Hierarchy of Transformations
为了实现复杂的变形，我们从最简单的一步一步开始。
首先我们进行粗糙的affine变形，之后对图像A到图像B使用了STN。之后进入第二个网络进行TPS细化形变。最终将这两个变形进行融合就得到了我们想要的结果。
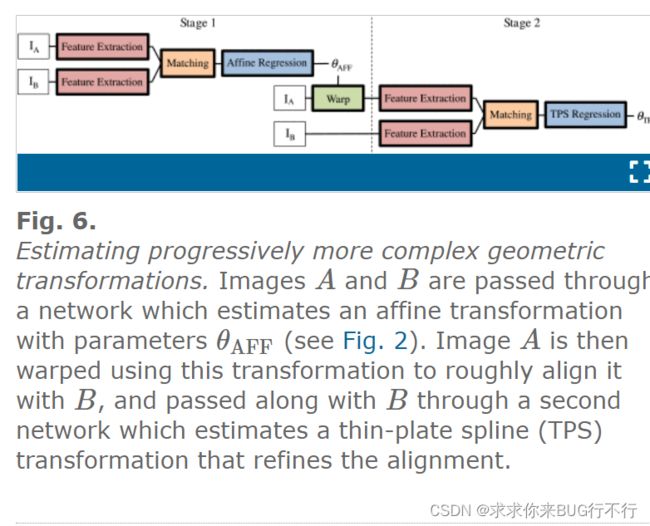
Iterative Refinement（迭代细化）
当形变比较大时，迭代次数少了得到的结果不佳，因此可以迭代多次，事实证明迭代多次效果较好。
Loss Function（损失函数）
使用每个栅格点经过使用预测参数和真实参数进行仿射变换后得到的值之间的距离作为Loss。
