Pytorch深度学习（三）：使用Pytorch实现线性回归

Pytorch深度学习（三）：使用Pytorch实现线性回归

• 参考B站课程：《PyTorch深度学习实践》完结合集
• 传送门：《PyTorch深度学习实践》完结合集

本文浅学Pytorch用法，并实现线性回归，最后比较DG、SDG、Adam等优化算法的误差收敛速度

一、预备知识

• 类与继承

• Pytorch手册

• scipy.io的使用

Tips：
下例中，我们创建的子类LinearModel继承了父类torch.nn.Module；

新写的类中需要重写forward()覆盖掉父类中的forward()；

由于魔法函数call的实现,model(xdata)将会调用model.forward(xdata)函数：

ypred = model(xdata)

也即最终

ypred = self.linear(x)

说forward最终是在torch.nn.Linear类中实现的，其形式为
$$\hat{y}=w\ast x+b$$
其中，$\hat{y}$ 是预测值，$x$ 是数据， $w$ 是权重（weight），$b$称为偏置（bias）

• 误差选取

$$loss=\sum _{n=1}^N(y_n-y{)}^2$$

criterion = torch.nn.MSELoss(reduction='sum')

而传统的

criterion = torch.nn.MSELoss(size_average = False) 

其中参数size_average将在新版本中删除，所以采用前者

• 优化器

optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)

其他优化器还有

• 反向传播

loss.backward()

• 参数（$w,b$）更新

optimizer.step()

• 调用scipy.io

import scipy.io as spio

spio.savemat('SGDerror.mat', mdict = {'SGD':costlist,
             'weight':model.linear.weight.item(),
             'bias':model.linear.bias.item()})

将相关数据储存成.mat文件，用于接下来比较各优化器性能

二、利用Pytorch做线性回归

import torch
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as spio
xdata = torch.Tensor([[1], [2], [3]])
ydata = torch.Tensor([[2], [4], [6]])

costlist = []

# LinearModel继承自nn.Module,必须创建_init_和forward覆盖父类
class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)

    def forward(self, x):
        ypred = self.linear(x)
        return ypred

model = LinearModel()

# criterion = torch.nn.MSELoss(size_average = False) 其中参数size_average将在新版本中删除
criterion = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)

for epoch in range(100):
    ypred = model(xdata)
    loss = criterion(ypred, ydata)
    print(epoch, loss.item())
    costlist.append(loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

print('w=', model.linear.weight.item())
print('b=', model.linear.bias.item())

spio.savemat('SGDerror.mat', mdict = {'SGD':costlist,
             'weight':model.linear.weight.item(),
             'bias':model.linear.bias.item()})

xtest = torch.Tensor([[4]])
ytest = model(xtest)
print('ypred=', ytest.data)

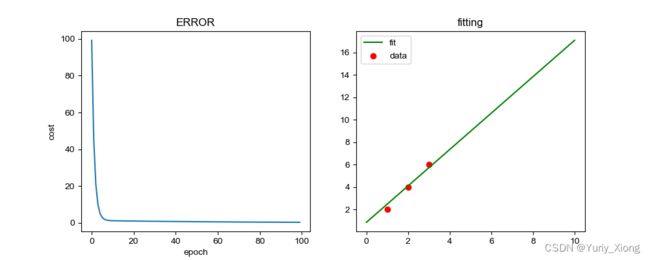
plt.figure(figsize=(10,4))
plt.subplot(1, 2, 1)
plt.plot(range(100), costlist)
plt.title('ERROR')
plt.xlabel('epoch')
plt.ylabel('cost')

plt.subplot(1, 2, 2)
xx = np.linspace(0,10,100)
yy = model.linear.weight.item()*xx + model.linear.bias.item()
plt.plot(xx, yy, label='fit', color = 'green')
plt.scatter(xdata, ydata, label='data', color = 'red')
plt.title('fitting')
plt.legend()
plt.show()

• 绘制图像
  

• 输出权重、偏置以及预测值

w= 1.7036523818969727
b= 0.6736679077148438
ypred= tensor([[7.4883]]）

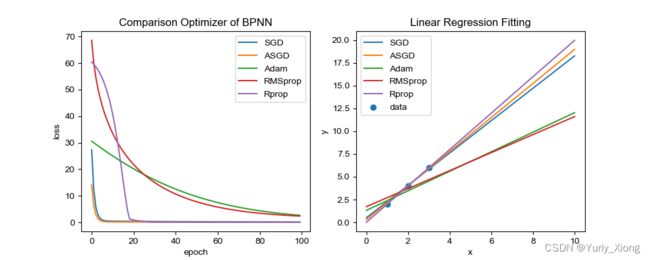
三、各优化器结果比较

如上我们利用scipy.io保存了各种优化器下产生的数据，再利用

spio.loadmat

导入各类数据，并绘制图像对比

import numpy as np
import torch
import matplotlib.pyplot as plt
import scipy.io as spio

dataSGD = spio.loadmat('SGDerror')
dataAdam = spio.loadmat('Adamerror')
dataASGD = spio.loadmat('ASGDerror')
dataRMSprop = spio.loadmat('RMSproperror')
dataRprop = spio.loadmat('Rproperror')

plt.figure(figsize=(10,4))

plt.subplot(1, 2, 1)
plt.plot(range(100), dataSGD['SGD'].reshape(100,), label='SGD')
plt.plot(range(100), dataASGD['ASDG'].reshape(100,), label='ASGD')
plt.plot(range(100), dataAdam['Adam'].reshape(100,), label='Adam')
plt.plot(range(100), dataRMSprop['RMSprop'].reshape(100,), label='RMSprop')
plt.plot(range(100), dataRprop['Rprop'].reshape(100,), label='Rprop')

plt.legend()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('Comparison Optimizer of BPNN')


plt.subplot(1, 2, 2)
x = np.linspace(0, 10, 100)
ySGD = dataSGD['weight'].item() * x + dataSGD['bias'].item()
yAdam = dataAdam['weight'].item() * x + dataAdam['bias'].item()
yASGD = dataASGD['weight'].item() * x + dataASGD['bias'].item()
yRMSprop = dataRMSprop['weight'].item() * x + dataRMSprop['bias'].item()
yRprop = dataRprop['weight'].item() * x + dataRprop['bias'].item()

xdata = [1, 2, 3]
ydata = [2, 4, 6]

plt.scatter(xdata, ydata, label='data')
plt.plot(x, ySGD,label = 'SGD')
plt.plot(x, yASGD, label= 'ASGD')
plt.plot(x, yAdam, label = 'Adam')
plt.plot(x, yRMSprop, label = 'RMSprop')
plt.plot(x, yRprop, label = 'Rprop')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title('Linear Regression Fitting')
plt.show()

• 生成图像
  
  在学习率（学习因子）$lr=0.01$ 的情况下，迭代100次，得到的结果显示，ASGD和SDG效果较好，其他结果见图像可知