基于二值数据的朴素贝叶斯手写数字识别 python代码实现
编程环境
python 3.10
numpy 1.23.4
matplotlib 3.6.1
原理解析
感觉 对于数学原理 使用文字表述的方式看起来太费劲 博主 参看的哔哩哔哩视频
讲解的还是比较清晰的,不过此篇博文讲解的多支特征二分类的问题,而我们手写数字识别使用的则是 二值数据的多分类,此处需要动一下脑子进行对应的转换。
[5分钟学算法] #02 朴素贝叶斯 写作业还得看小明_哔哩哔哩_bilibili
编程思路
首先对某一张图片进行二值化,使得图片矩阵中只出现0、1类别的数字 代码如下
def binaryzation(img):
img_data = np.zeros((img.shape))
h, w = img.shape
for i in range(h):
for j in range(w):
if img[i][j] == 0:
img_data[i][j] = 0
else:
img_data[i][j] = 1
return img_data跟据cnn_h,cnn_w对图片的数据矩阵完成分块,统计某个分块中1所占的比例,根据阙值决定提取的特征为1或者为0,最后所得特征矩阵为 28/cnn_w * 28/cnn_h
def features_out(img_data, cnn_h, cnn_w, threshold):
h, w = img_data.shape
features_data = np.zeros((int(h / cnn_h), int(w / cnn_w)))
for index_h in range(0, h, cnn_h):
for index_w in range(0, h, cnn_w):
count = 0
for i in range(index_h, index_h + cnn_h):
for j in range(index_w, index_w + cnn_w):
if img_data[i][j] == 1:
count = count + 1
# 划分的格子统计完成
flag = count / (cnn_w * cnn_h)
if flag > threshold:
features_data[int(index_h / cnn_h)][int(index_w / cnn_w)] = 1
else:
features_data[int(index_h / cnn_h)][int(index_w / cnn_w)] = 0
return features_data然后根据训练集的数量以及每一个类别中样本的数量计算先验概率
def compute_pre_odds(scale):
# 训练集总样本数
train_count = 0
for i in range(0, 10):
train_count = train_count + len(os.listdir(DATA_PATH + str(i)))
train_count = int(train_count * scale)
# 统计先验概率
for i in range(0, 10):
pre_odds.append((len(os.listdir(DATA_PATH + str(i))) * scale) / train_count)进而计算 某一类图片的类条件概率,最后每一个类别根据计算得到一个 (1,28/cnn_w * 28/cnn_h)维度的特征向量,内部对应位置存储的是,某一类别中某一个维度的特征取1的概率
def train_model(scale, cnn_h, cnn_w, threshold):
# 二值化 + 特征提取
temp_features = np.zeros((int(28 / cnn_h), int(28 / cnn_w)))
for i in range(0, 10):
# 获取单独文件夹下的所有文件列表
dir_list = os.listdir(DATA_PATH + str(i))
for j in range(0, int(len(dir_list) * scale)):
# 处理训练集中的数据 (二值化 + 特征提取)
image = images.imread(DATA_PATH + str(i) + "/" + dir_list[j])
temp_features = temp_features + features_out(binaryzation(image), cnn_h, cnn_w, threshold)
# 计算 每一类图片数据中 每一个维度的 特征概率
# 拉普拉斯平滑 (防止出现概率为0的事件)
temp_features = (temp_features + 1) / (int(len(dir_list) * scale) + 2)
pwj.append(temp_features.reshape(1, int(28 / cnn_h) * int(28 / cnn_w)))
temp_features = temp_features * 0 # 临时数组 初始化进行案例测试的时候,根据先前计算的先验概率、类条件概率以及朴素贝叶斯公式进行类别概率的计算 返回预测的最大可能性
def model_test(image_path, cnn_h, cnn_w, threshold):
# 先用一个测试样本进行测试
test_data = features_out(binaryzation(images.imread(image_path)), cnn_h, cnn_w,
threshold)
# 将test_data 转化为 1*196 维度的特征向量
predict_data = test_data.reshape((1, int(28 / cnn_h * 28 / cnn_w)))
# 已经获取到一个测试样本经过处理的特征矩阵 14*14 的二维矩阵
# 开始根据某一类别条件下进行运算的结果
predict_odds = []
for i in range(10):
predict_sum = pre_odds[i]
for j in range(int(28 / cnn_h) * int((28 / cnn_w))):
# 根据贝叶斯公式进行概率的计算
if predict_data[0][j] == 1:
predict_sum = predict_sum * pwj[i][0][j]
else:
predict_sum = predict_sum * (1 - pwj[i][0][j])
predict_odds.append(predict_sum)
# 函数直接返回预测结果
return predict_odds.index(max(predict_odds))代码原理解析
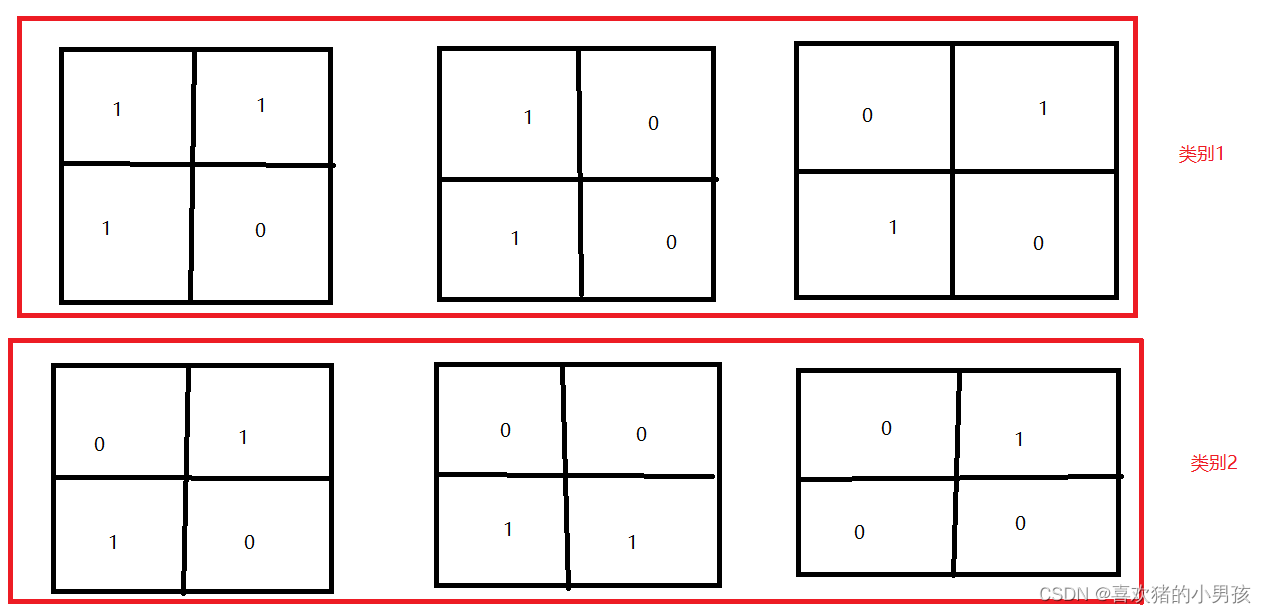
假设一共有两类数字进行识别,此时每一张图片都划分为 2*2 的四个格子,那么此时每一张图片提取出来的特征向量即为4个格子 经过维度转换 成为 1*4的一维向量。
此时某一类训练集中有3张图片 那么我们一共提取到了3个4维向量 如下图所示
此时 我们计算先验概率 就很简单 训练集 有两类 每一类都有 三个样本 则二者的先验概率皆为0.5.
那么我们来看类条件概率,也即 P(wi,|x=类别1)的概率 注意下图黄色圈圈中的内容
那么由此可知,类别一的第一维度的条件概率为 2/3 也就是 p(x1 | w=类别一) = 2/3
而且当我们计算类别一第三 , 四维度的的类条件概率的时候 出现了 概率 1 | 0 这对后续的计算会产生极大的影响,所以我们一般会使用拉普拉斯平滑算法进行校正。
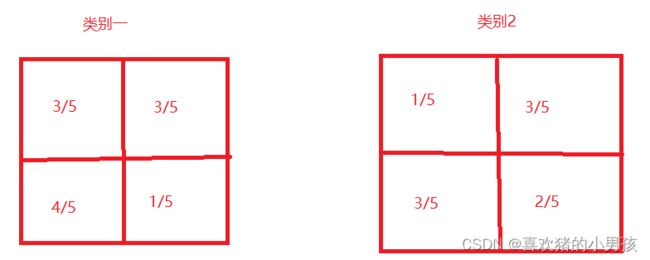
也就是所有的分子都+1 分母都+特征取值数量(此处的特征取值数量只有 0和1 所以分母需要进行+2)此时 我们上述的计算就会发生变化 p(x1 | w=类别一) = 2/3 经过拉普拉斯平滑之后 会变成 p(x1 |w=类别一) = 3/5 而且 有 p(x3 | w=类别一) = 4/5 p(x4 | w=类别一) = 1/5
之后 对所有的类别中的所有图片的所有维度都进行类条件概率计算 最后得到两个 概率向量 如下图所示。
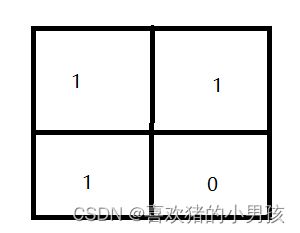
当一个测试样本经过特征提取后的矩阵如下图所示的时候 进行 预测。
贝叶斯公式
p(w=类别一 | x) = p(w=类别一) * p(x | w = 类别一) / p(类别一)* p(x | w = 类别一) + p(类别二)* p(x | w = 类别二)
根据朴素贝叶斯公式进行类推得到如下的计算结果 即可 得到 某一类别后验概率的等价大小数值为
p(w=类别一 | x) = 3/5 * 3/5 * 4/5 * (1-1/5) = 0.2304
p(w = 类别二 | x) = 4/5 * 3/5 * 3/5 * (1-2/5) = 0.1728
此时 我们判断 测试样本的数据 属于 类别一
所有代码
import numpy as np
import matplotlib.image as images
import os
DATA_PATH = "data/mnist40/" # 数据集地址
pre_odds = [] # 存储先验概率
pwj = [] # 存储的都是每一类数字的每一维度特征为1的概率 内部存储的都是 1*196维度的特征
'''
图片进行二值化预处理
参数 (图片数据)
返回 图片数据
'''
def binaryzation(img):
img_data = np.zeros((img.shape))
h, w = img.shape
for i in range(h):
for j in range(w):
if img[i][j] == 0:
img_data[i][j] = 0
else:
img_data[i][j] = 1
return img_data
'''
特征提取方法 根据传递的参数 进行 一张图片的特征提取
参数 (图片数据 划分的小格子的高度 划分的小格子的宽度 阙值 )
返回 某一张图片的特征矩阵
'''
def features_out(img_data, cnn_h, cnn_w, threshold):
h, w = img_data.shape
features_data = np.zeros((int(h / cnn_h), int(w / cnn_w)))
for index_h in range(0, h, cnn_h):
for index_w in range(0, h, cnn_w):
count = 0
for i in range(index_h, index_h + cnn_h):
for j in range(index_w, index_w + cnn_w):
if img_data[i][j] == 1:
count = count + 1
# 划分的格子统计完成
flag = count / (cnn_w * cnn_h)
if flag > threshold:
features_data[int(index_h / cnn_h)][int(index_w / cnn_w)] = 1
else:
features_data[int(index_h / cnn_h)][int(index_w / cnn_w)] = 0
return features_data
'''
计算先验概率
参数 (训练集比例)
无需返回 存储为全局变量
'''
def compute_pre_odds(scale):
# 训练集总样本数
train_count = 0
for i in range(0, 10):
train_count = train_count + len(os.listdir(DATA_PATH + str(i)))
train_count = int(train_count * scale)
# 统计先验概率
for i in range(0, 10):
pre_odds.append((len(os.listdir(DATA_PATH + str(i))) * scale) / train_count)
'''
模型训练 计算 每一类的每一维度特征的类条件概率 以及 先验概率
参数 (训练集比例 划分的小格子的高度 划分的小格子的宽度 阙值 )
无需返回 将 此方法计算所得数据 存储为 全局变量
'''
def train_model(scale, cnn_h, cnn_w, threshold):
# 二值化 + 特征提取
temp_features = np.zeros((int(28 / cnn_h), int(28 / cnn_w)))
for i in range(0, 10):
# 获取单独文件夹下的所有文件列表
dir_list = os.listdir(DATA_PATH + str(i))
for j in range(0, int(len(dir_list) * scale)):
# 处理训练集中的数据 (二值化 + 特征提取)
image = images.imread(DATA_PATH + str(i) + "/" + dir_list[j])
temp_features = temp_features + features_out(binaryzation(image), cnn_h, cnn_w, threshold)
# 计算 每一类图片数据中 每一个维度的 特征概率
# 拉普拉斯平滑 (防止出现概率为0的事件)
temp_features = (temp_features + 1) / (int(len(dir_list) * scale) + 2)
pwj.append(temp_features.reshape(1, int(28 / cnn_h) * int(28 / cnn_w)))
temp_features = temp_features * 0 # 临时数组 初始化
'''
模型测试 使用先前计算的类条件概率 以及 先验概率 分别计算 十个类别的可能性
参数 (图片地址 划分的小格子的高度 划分的小格子的宽度 阙值 )
返回 预测结果
'''
def model_test(image_path, cnn_h, cnn_w, threshold):
# 先用一个测试样本进行测试
test_data = features_out(binaryzation(images.imread(image_path)), cnn_h, cnn_w,
threshold)
# 将test_data 转化为 1*196 维度的特征向量
predict_data = test_data.reshape((1, int(28 / cnn_h * 28 / cnn_w)))
# 已经获取到一个测试样本经过处理的特征矩阵 14*14 的二维矩阵
# 开始根据某一类别条件下进行运算的结果
predict_odds = []
for i in range(10):
predict_sum = pre_odds[i]
for j in range(int(28 / cnn_h) * int((28 / cnn_w))):
# 根据贝叶斯公式进行概率的计算
if predict_data[0][j] == 1:
predict_sum = predict_sum * pwj[i][0][j]
else:
predict_sum = predict_sum * (1 - pwj[i][0][j])
predict_odds.append(predict_sum)
# 函数直接返回预测结果
return predict_odds.index(max(predict_odds))
'''
此方法用于最后计算模型的预测结果 以及 统计预测准确率使用ca
参数 (提取特征使用的阙值 划分的小格子的高度 划分的小格子的宽度 训练集占比)
返回 预测的准确率
'''
def compute_acc(threshold, cnn_h, cnn_w, scale):
acc_count = 0
count = 0
for i in range(10):
files = os.listdir(DATA_PATH + str(i))
for j in range(int(len(files) * scale), int(len(files))):
# 拼接 image_path 传递给预测函数
image_path = DATA_PATH + str(i) + "/" + files[j - int(len(files) * scale)]
predict_result = model_test(image_path, cnn_h, cnn_w, threshold)
# 输出预测结果
# print("预测结果为:", predict_result, " 真实结果为:", i)
if predict_result == i:
acc_count += 1
# 统计测试样本数量
count += 1
# 统计测试样本总个数 最后输出预测准确率
print("测试样本个数为:", count, "预测正确的统计数量为:", acc_count)
return acc_count / count
'''
整合方法 根据所需进行调整
'''
def model(scale, cnn_h, cnn_w, threshold):
# 计算先验概率 参数 (训练集占比)
compute_pre_odds(scale)
# 所有图片训练集的图片进行二值化 以及 特征提取
train_model(scale, cnn_h, cnn_w, threshold)
acc = compute_acc(threshold, cnn_h, cnn_w, scale)
print("预测准确率为:", '{:.2%}'.format(acc))
return round(acc, 4)
if __name__ == '__main__':
temp = []
for i in range(5, 95, 2):
acc = model(scale=i / 100, cnn_h=2, cnn_w=2, threshold=0.1)
temp.append(acc)
print(temp)
最后附上gitee代码空间 以及 数据集 可以从以下地址空间获取
spider_test: python 爬chong练习 - Gitee.com