Python 实现朴素贝叶斯代码演示
朴素贝叶斯可以细分为三种方法:分别是伯努利朴素贝叶斯、高斯朴素贝叶斯和多项式朴素贝叶斯。下文就这三种方法进行详细讲解和演示。
目录
一、伯努利朴素贝叶斯方法
1.1 例子解答
1.1.1 代码:
1.1.2 结果:
二、高斯朴素贝叶斯方法
2.1 解题
2.1.1 代码:
2.1.2 结果:
2.2 检查高斯朴素贝叶斯的正确率
2.2.1 代码:
2.2.2 结果:
三、多项式朴素贝叶斯方法
3.1 多项式朴素贝叶斯实现新闻文本分类
3.1.1 代码
3.1.2 结果
3.2 检测正确率
3.2.1 代码
3.2.2结果
一、伯努利朴素贝叶斯方法
伯努利朴素贝叶斯是假定样本特征的条件概率分布服从二项分布,即“0-1分布”。
1.1 例子解答
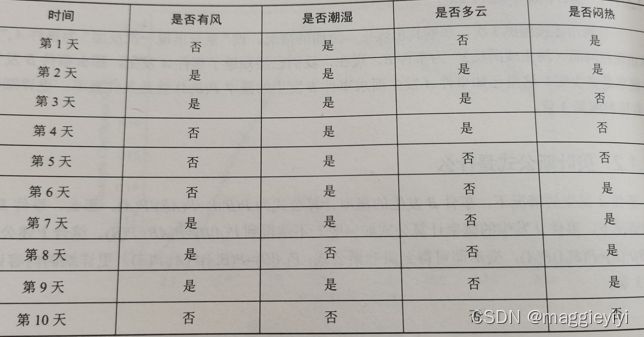
例如利用伯努利朴素贝叶斯预测天气会不会下雨:
其中有雨用1标识,无雨用0标识。
各种属性则是用1标识,否用0标识。一直上表的下雨情况为Y=[1,1,1,1,0,1,1,0]
问(无风,不潮湿,多云,不闷热)的情况是否下雨。
这里可以将预测数据设为x_pre=[0,0,1,1]
1.1.1 代码:
import numpy as np
x = np.array([[0,1,0,1],[1,1,1,1],[1,1,1,0],[0,1,1,0],[0,1,0,0],[0,1,0,1],
[1,1,0,1],[1,0,0,1],[1,1,0,1],[0,0,0,0]])
y = np.array([1,1,1,1,0,1,0,1,1,0])
from sklearn.naive_bayes import BernoulliNB
bnb = BernoulliNB()
bnb.fit(x,y)
day_pre=[[0,0,1,0]]
pre = bnb.predict(day_pre)
print("预测结果如下\n:",'*'*50)
print('结果为:',pre)
print('*'*50)
#进一步查看概率分布
pre_pro = bnb.predict_proba(day_pre)
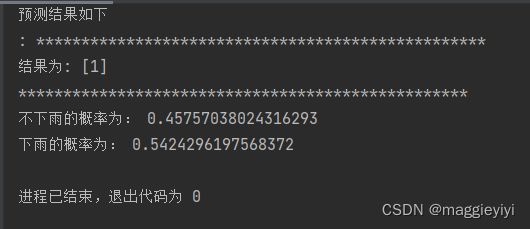
print("不下雨的概率为:",pre_pro[0][0],"\n下雨的概率为:",pre_pro[0][1])1.1.2 结果:
二、高斯朴素贝叶斯方法
高斯朴素贝叶斯分类器是假定样本特征符合高斯分布时常用的算法。高斯分布也称为正态分布。如果随机变量X服从一个数学期望μ、方差的正态分布。可以直接调用sklearn.native_bayes.GuassianNB().
2.1 解题
上述题用高斯朴素贝叶斯方法预测的结果如下:
2.1.1 代码:
import numpy as np
x = np.array([[0,1,0,1],[1,1,1,1],[1,1,1,0],[0,1,1,0],[0,1,0,0],[0,1,0,1],
[1,1,0,1],[1,0,0,1],[1,1,0,1],[0,0,0,0]])
y = np.array([1,1,1,1,0,1,0,1,1,0])
# from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(x,y)
day_pre=[[0,0,1,0]]
pre = gnb.predict(day_pre)
print("预测结果如下\n:",'*'*50)
print('结果为:',pre)
print('*'*50)
#进一步查看概率分布
pre_pro = gnb.predict_proba(day_pre)
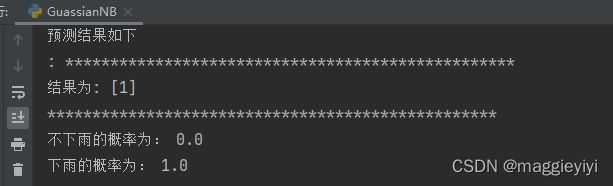
print("不下雨的概率为:",pre_pro[0][0],"\n下雨的概率为:",pre_pro[0][1])2.1.2 结果:
2.2 检查高斯朴素贝叶斯的正确率
利用sklearn自带的数据集来展示高斯朴素贝叶斯来验证正确率:
2.2.1 代码:
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
x,y = make_blobs(n_samples = 800,centers = 6,random_state = 6)
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25,random_state=33)
gnb = GaussianNB()
gnb.fit(x_train,y_train)
print('-'*50)
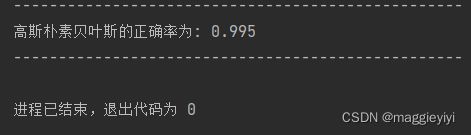
print('高斯朴素贝叶斯的正确率为:',gnb.score(x_test,y_test))
print('-'*50)2.2.2 结果:
三、多项式朴素贝叶斯方法
多项式朴素贝叶斯是假定样本特征符合多项式分布时常用的算法,把一个二项式公式推广至多种状态,就得到了多项分布。例如骰子。
3.1 多项式朴素贝叶斯实现新闻文本分类
以sklearn.datasets中的新闻文本数据集为例,展示朴素贝叶斯分类方法。
其中sklearn.dates中的fetch_20newsgroups数据集一共射击20个话题,进行预测分类。
3.1.1 代码
#加载数据
from sklearn.datasets import fetch_20newsgroups
newsgroups = fetch_20newsgroups(subset='all')
x = newsgroups.data
y = newsgroups.target
#查看目标
print('目标变量:\n',newsgroups.target_names)
#查看特征变量情况
print('特征变量示例:\n',x[0])
#查看特征变量目标
print('特征变量目标:\n',y)
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3,random_state=33)
from sklearn.feature_extraction.text import CountVectorizer
vec = CountVectorizer()
x_vec_train = vec.fit_transform(x_train)
x_vec_test = vec.transform(x_test)
from sklearn.naive_bayes import MultinomialNB
mnb = MultinomialNB()
mnb.fit(x_vec_train,y_train)
mnb_y_predict = mnb.predict(x_vec_test)
from sklearn.metrics import classification_report
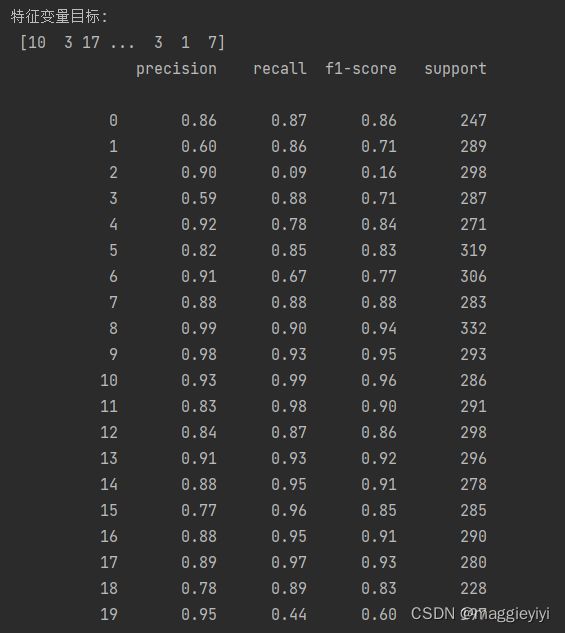
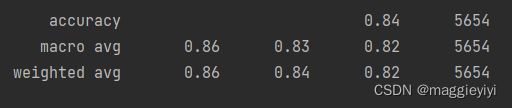
print(classification_report(y_test,mnb_y_predict))3.1.2 结果
3.2 检测正确率
3.2.1 代码
from sklearn.datasets import make_blobs
import numpy as np
#自带数据集
x,y = make_blobs(n_samples=800,centers=6,random_state=6)
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25,random_state=33)
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(x_train)
x_train_s = scaler.transform(x_train)
x_test_s = scaler.transform(x_test)
from sklearn.naive_bayes import MultinomialNB
mnb = MultinomialNB()
mnb.fit(x_train_s,y_train)
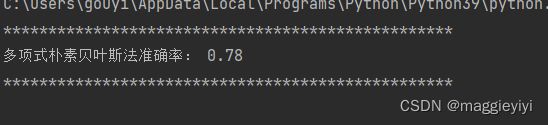
print('*'*50)
print('多项式朴素贝叶斯法准确率:',mnb.score(x_test_s,y_test))
print('*'*50)3.2.2结果