pytorch的F.cross_entropy交叉熵函数和标签平滑函数
pytorch的F.cross_entropy交叉熵函数和标签平滑函数
F.cross_entropy
先来讲下基本的交叉熵cross_entropy,官网如下:torch.nn.functional.cross_entropy — PyTorch 1.12 documentation
torch.nn.functional.cross_entropy(input, target, weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction='mean', label_smoothing=0.0)
loss=F.cross_entropy(input, target)
从官网所给的资料及案例,可以知道计算交叉熵函数的主要为两个:
N:样本个数,C:类别数
-
input是(N,C),target是(N),其中target里的每个元素值0<= i <= C-1,标明它属于哪个类别
# Example of target with class indices input = torch.randn(3, 5, requires_grad=True) # input[i][j]表示第i个样本第j个类别的score target = torch.randint(5, (3,), dtype=torch.int64) # target[i]表示第i个样本的类别,此处0<= target[i] <= C - 1 loss = F.cross_entropy(input, target) -
input是(N,C),target是(N,C),这就是常见的向量之间计算间隔距离
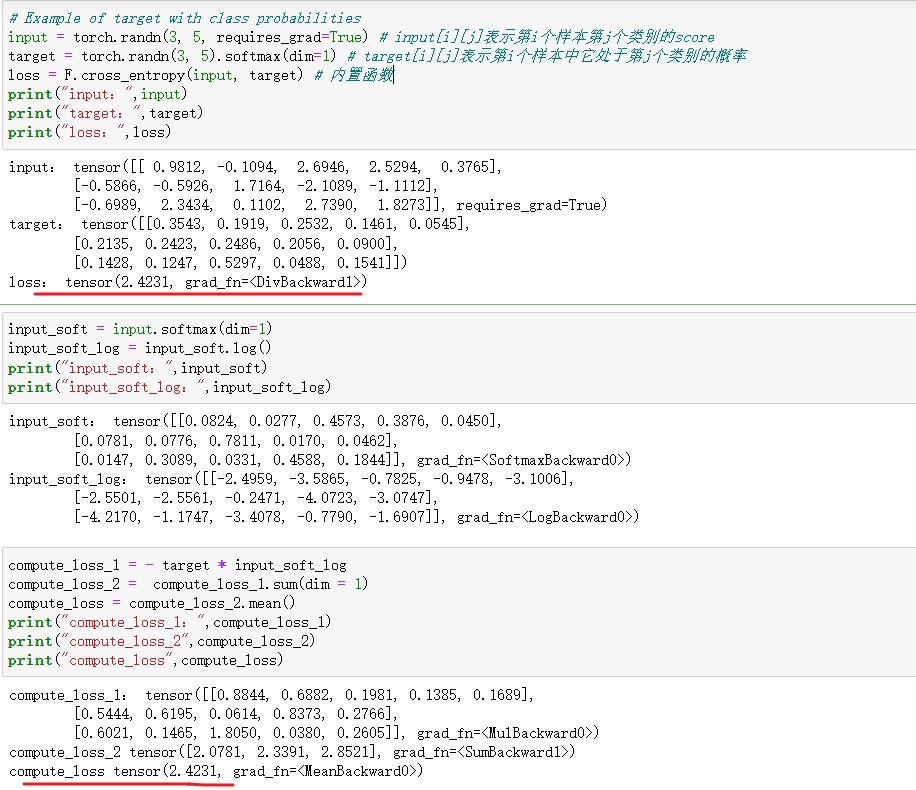
# Example of target with class probabilities input = torch.randn(3, 5, requires_grad=True) # input[i][j]表示第i个样本第j个类别的score target = torch.randn(3, 5).softmax(dim=1) # target[i][j]表示第i个样本中它处于第j个类别的概率 loss = F.cross_entropy(input, target)
交叉熵的公式如下:
H ( p , q ) = − ∑ i P ( i ) l o g Q ( i ) ,其中 P 为真实值, Q 为预测值, i 是第 i 个类别 H(p,q) = - \sum_i P(i)log Q(i),其中P为真实值,Q为预测值,i是第i个类别 H(p,q)=−i∑P(i)logQ(i),其中P为真实值,Q为预测值,i是第i个类别
样例1,cross_entropy计算步骤如下(以下面那种图片为例子):
-
对input按列先进行softmax,将score转化为 -> 每个样本出现第j个类别的概率。得到input_soft
S o f t m a x ( z i ) = e x p ( z i ) ∑ j e x p ( z j ) Softmax(z_i) = \frac{exp(z_i)}{\sum_j exp(z_j)} Softmax(zi)=∑jexp(zj)exp(zi) -
对input_soft进行log运算,记为input_soft_log
-
对input_soft_log与真实值target进行处理
-
先将target先进行one-hot编码,我们有
target = [[0 0 0 0 1], [0 0 1 0 0], [0 1 0 0 0]] -
计算第一个样本的损失,这里:P = [0 0 0 0 1],Q = [0.0681, 0.1033, 0.1193, 0.5755, 0.1338],logQ = [-2.6872, -2.2704, -2.1259, -0.5525, -2.0114]
-
由交叉熵公式可得,第一个样本的损失,在这里直接找到为1的类别就好了
H ( p , q ) = − ∑ i P ( i ) l o g Q ( i ) = − ( 0 ∗ − 2.6872 + . . . + 1 ∗ − 2.0114 ) = 2.0114 = − l o g Q ( 4 ) H(p,q) = - \sum_i P(i)log Q(i) = - (0 * -2.6872 + ...+ 1 * -2.0114) = 2.0114 = - log Q(4) H(p,q)=−i∑P(i)logQ(i)=−(0∗−2.6872+...+1∗−2.0114)=2.0114=−logQ(4) -
同理可得,第二、第三个样本损失为:- logQ(2)、-logQ(1)
-
最后计算每个样本的均值
-
对于样例2,一样的计算,就是在标签哪里不再是one-hot编码,变为了概率.。P值进行了替换罢了
标签平滑损失
主要用于多标签分类模型正则化
标签平滑是一种损失函数的修正,它将神经网络的的训练目标从“1”调整为“1 - label smoothing adjustment”,这意味着神经网络被训练得对自己的答案不是那么自信,NN有一个坏习惯,在训练过程中对预测变得“过于自信”,这可能会降低它们的泛化能力,从而在新的、看不见的未来数据上表现得同样“出色”,此外,大型数据集通常会包含标签错误的数据,这意味着神经网络在本质上应该对“正确答案”持怀疑态度,以减少一定程度上围绕错误答案的极端情况下建模。
增加label smooting真实的概率分布变为:
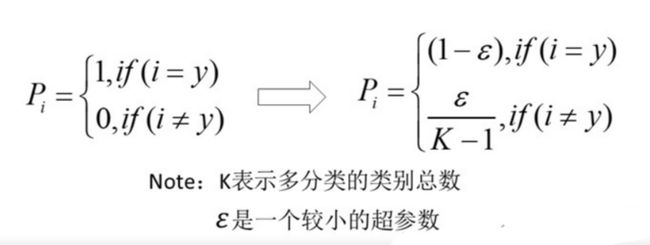
交叉熵损失函数变为:
这里有多种版本的实现:python - Label Smoothing in PyTorch - Stack Overflow
PyTorch官方实现:CrossEntropyLoss — PyTorch 1.12 documentation
torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction='mean', label_smoothing=0.0)
从多种版本中挑选一种实现,完整代码如下:
import torch as nn
import torch.nn.functional as F
class LabelSmoothingLoss(nn.Module):
'''LabelSmoothingLoss
'''
def __init__(self, smoothing=0.05, dim=-1):
super(LabelSmoothingLoss, self).__init__()
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.dim = dim
def forward(self, pred, target):
pred = pred.log_softmax(dim=self.dim)
num_class = pred.size()[-1]
with torch.no_grad():
true_dist = torch.zeros_like(pred)
true_dist.fill_(self.smoothing / (num_class - 1))
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
return torch.mean(torch.sum(-true_dist * pred, dim=self.dim))
参考链接:
label smoothing(标签平滑)学习笔记 - 知乎 (zhihu.com)
(433条消息) 对PyTorch中F.cross_entropy()函数的理解_爬虫叁号的博客-CSDN博客
标签平滑&深度学习:Google Brain解释了为什么标签平滑有用以及什么时候使用它 - 知乎 (zhihu.com)
python - Label Smoothing in PyTorch - Stack Overflow