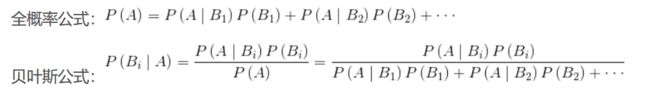朴素贝叶斯的详细讲解及其Python实现
公式介绍
朴素贝叶斯概述
朴素贝叶斯法基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入输出的联合概率分布,然后基于此模型,对给定的输入 X, 利用贝叶斯定理求出后验概率最大的输出 u。
朴素贝叶斯公式推导
朴素贝叶斯法的参数估计
拉普拉斯平滑
用极大似然估计可能会出现所要估计的概率值为 0 的情况。 这时会影响到后验概率的计算结果,使分类产生偏差。解决这一问题可以采用拉普拉斯平滑
举个经典例子:
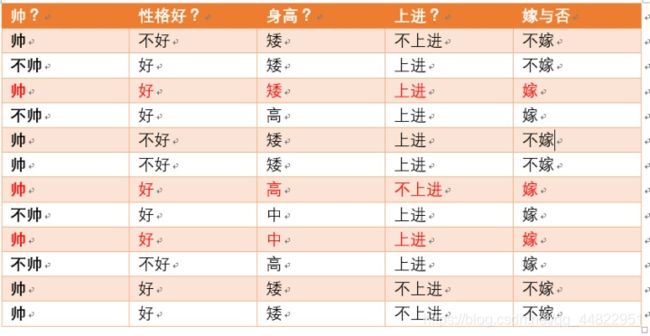
数据如下
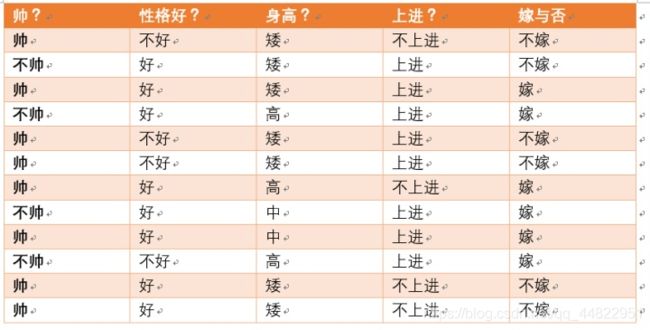 在这个数据中有4个特征 假设它们的取值是这样的 帅{帅,不帅} 性格好{非常好,好,不好} 身高{高,矮} 上进{上进,不上进}
在这个数据中有4个特征 假设它们的取值是这样的 帅{帅,不帅} 性格好{非常好,好,不好} 身高{高,矮} 上进{上进,不上进}
现在假设有个男生帅,性格非常好,身高 高 上进 问 女生是否嫁
即比较P(嫁| 帅,性格非常好,身高高,上进)与 P(不嫁| 帅,性格非常好,身高高,上进) 的大小
P(嫁| 帅,性格非常好,身高高,上进)> P(不嫁| 帅,性格非常好,身高高,上进) 嫁
P(嫁| 帅,性格非常好,身高高,上进)< P(不嫁| 帅,性格非常好,身高高,上进) 不嫁
按朴素贝叶斯公式可以得到

而当我们重新观察数据
 会发现我们的训练数据中并没有性格是 非常好的数据 这也导致P(性格非常好| 嫁)的概率为0 进而导致P(嫁| 帅,性格非常好,身高高,上进)的概率为0 而在日常生活中我们知道 一个男生如果帅,性格非常好,身高高,上进 绝对是一个完美对象 嫁的概率绝对不是0 。所以为了避免这种问题 引进了拉普拉斯平滑。它的思想非常简单,就是对每个类别下所有划分的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响,并且解决了上述频率为0的尴尬局面。
会发现我们的训练数据中并没有性格是 非常好的数据 这也导致P(性格非常好| 嫁)的概率为0 进而导致P(嫁| 帅,性格非常好,身高高,上进)的概率为0 而在日常生活中我们知道 一个男生如果帅,性格非常好,身高高,上进 绝对是一个完美对象 嫁的概率绝对不是0 。所以为了避免这种问题 引进了拉普拉斯平滑。它的思想非常简单,就是对每个类别下所有划分的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响,并且解决了上述频率为0的尴尬局面。
![]()
第j特征的个数是这样理解的 比如帅有 不帅 和帅 两个值 则特征的个数是2
加入拉普拉斯平滑后
朴素贝叶斯对连续值处理
通过前面的学习我们可以了解到 朴素贝叶斯对值为离散类型的特征去计算概率会比较方便,但是实际我们在应用的时候 不可避免地用到取值为连续值的特征如
| 身高 (英尺) | 体重(磅) | 脚长(英寸) | 性别 |
|---|---|---|---|
| 6 | 180 | 12 | 男 |
| 5.92 | 190 | 11 | 男 |
| 5.58 | 170 | 12 | 男 |
| 5.92 | 165 | 10 | 男 |
| 5 | 100 | 6 | 女 |
| 5.5 | 150 | 8 | 女 |
| 5.42 | 130 | 7 | 女 |
| 5.75 | 150 | 9 | 女 |
对于这些取值为连续值的特征,我们可以假设这些特征的取值服从正态分布。在以上的例子中,我们可以假设身高,体重,脚长都服从正态分布
通过其样本集计算出均值和方差,也就是得到正态分布的密度函数。有了密度函数,就可以把值代入,算出某一点的密度函数的值。
如 男性的身高是均值5.855、方差0.035的正态分布
如果一个人的身高是6英尺我们就可以预测他是男性的概率

python实现朴素贝叶斯算法
训练过程


数据来源于和鲸社区

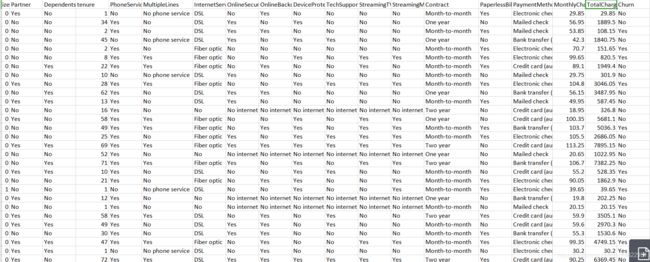 因为数据中大多数特征值是离散的 并且是以自然语言的形式呈现的 比如
因为数据中大多数特征值是离散的 并且是以自然语言的形式呈现的 比如
OnlineSecurity有三种取值No,Yes,No internet service,可以用LabelEncoder来编码 结果是以数字0,1,2分别代表这三种类型 对所有值是离散类型的特征都采用这种方法来处理
def datapreprocessing(data):#数据预处理
le = LabelEncoder()
data['gender'] = le.fit_transform(data['gender'].values)
data['Partner'] = le.fit_transform(data['Partner'].values)
data['Dependents'] = le.fit_transform(data['Dependents'].values)
data['PhoneService'] = le.fit_transform(data['PhoneService'].values)
data['MultipleLines'] = le.fit_transform(data['MultipleLines'].values)
data['InternetService'] = le.fit_transform(data['InternetService'].values)
data['OnlineSecurity'] = le.fit_transform(data['OnlineSecurity'].values)
data['OnlineBackup'] = le.fit_transform(data['OnlineBackup'].values)
data['DeviceProtection'] = le.fit_transform(data['DeviceProtection'].values)
data['TechSupport'] = le.fit_transform(data['TechSupport'].values)
data['StreamingTV'] = le.fit_transform(data['StreamingTV'].values)
data['StreamingMovies'] = le.fit_transform(data['StreamingMovies'].values)
data['Contract'] = le.fit_transform(data['Contract'].values)
data['PaperlessBilling'] = le.fit_transform(data['PaperlessBilling'].values)
data['PaymentMethod'] = le.fit_transform(data['PaymentMethod'].values)
data['Churn'] = le.fit_transform(data['Churn'].values)
print(data)
data.to_csv('Customer-Churn.csv')#
TotalCharges这一列有空白值 首先用0填充缺失值,以把这一列的数据类型由字符串转换为浮点型 之后求出这一列的平均值来取代为0的值
df=read_data("Customer-Churn.csv")#读数据
df['TotalCharges'] = df['TotalCharges'].replace(" ", "0")#TotalCharges中有空格
df['TotalCharges'] = pd.to_numeric(df['TotalCharges'])
TotalCharges = []
for i in range(df.shape[0]):
TotalCharges.append(float(df.loc[i, 'TotalCharges'])) # 将字符串数据转化为浮点型加入到数组之中
avg=np.var(TotalCharges)
df['TotalCharges'] = df['TotalCharges'].replace(0, avg)#用均值填充缺失值
划分特征和标签 并对数据进行标准化处理
def prepare_data(df):#数据预处理
ndarray_data = df.values
X=df.iloc[:,2:21]#数据切片
Y=df.iloc[:,21]
return X , Y
朴素贝叶斯模型
class Bayes:
def __init__(self,X_train,Y_train,X_test,Y_test):
self.X_train=X_train
self.Y_train=Y_train
self.X_test=X_test
self.Y_test=Y_test
def calculate_prior_probability(self,c):#计算先验概率 计算 Y=c的先验概率 Y是标签集合
N = self.Y_train.shape[0]
label=self.classification(self.Y_train)
num=label[c]
return num/N
def classification(self,Y):
N = Y.shape[0] # 一共有多少条数据
label = {}#用一个列表存储每种分类的数据共有多少条
for i in range(N):
if Y[i][0] in label:
label[Y[i][0]] += 1
else:
label[Y[i][0]] = 1
return label
def fit(self,X):#预测X的标签
label=self.classification(self.Y_train)
classs=label.keys() # 返回键的集合 都有哪些标签
list={}
max=0
maxc=0
for c in classs:
p1=self.discrete_features(X[0],c,0)
p2 =self.discrete_features( X[1], c, 1)
p3=self.discrete_features( X[2], c, 2)
p4 = self.discrete_features( X[3], c, 3)
p5 = self.continuous_feature( X[4], c, 4)
p6 = self.discrete_features( X[5], c, 5)
p7 = self.discrete_features(X[6], c, 6)
p8 = self.discrete_features( X[7], c, 7)
p9 = self.discrete_features(X[8], c, 8)
p10 = self.discrete_features( X[9], c, 9)
p11 = self.discrete_features( X[10], c, 10)
p12 = self.discrete_features( X[11], c, 11)
p13 = self.discrete_features( X[12], c, 12)
p14 = self.discrete_features( X[13], c, 13)
p15 = self.discrete_features( X[14], c, 14)
p16 = self.discrete_features( X[15], c, 15)
p17 = self.discrete_features(X[16], c, 16)
p18 = self.continuous_feature(X[17], c, 17)
p19 = self.continuous_feature(X[18], c, 18)
probability=p1*p2*p3*p4*p5*p6*p7*p8*p9*p10*p11*p12*p13*p14*p15*p16*p17*p18*p19*self.calculate_prior_probability(c)
list[c]= probability
for k,v in list.items():
if v>max:
max=v
maxc=k
return maxc
def predict(self): # 测试模型的准确率
n = self.X_test.shape[0] # 共有多少条数据
num = 0 # 正确预测的数据有多少
for i in range(self.X_test.shape[0]):
print(i)
X = self.X_test[i]
Y = self.Y_test[i]
c= self.fit(X)
if c==Y[0]:
num += 1
return num / n
def discrete_features(self,v,c,col):#离散类型特征 特征值 标签值 col表明是哪个特征
m=self.X_train.shape[0]
label=self.classification(self.Y_train)
N=label[c] #这个标签的数据共有多少条
num=0# label=c 且 第col特征 取值为v的数据共有多少条
classs={} # 对于第col特征来说 它的不同取值都有什么 分别有多少条数据
for i in range(m):
if self.X_train[i][col] in classs:
classs[self.X_train[i][col]]+=1
else:
classs[self.X_train[i][col]] =1
if self.X_train[i][col]==v and self.Y_train[i]==c:
num+=1
b=len(classs)
# print(b)
return (num+1)/(N+b) #使用拉普拉斯平滑
def continuous_feature(self,v,c,col):#连续类型特征 特征值 标签值 col表明是哪个特征
m = self.X_train.shape[0]
list=[]
sum=0
for i in range(m):
if self.Y_train[i][0]==c:
sum+=self.X_train[i][col]
list.append(self.X_train[i][col])
avg=sum/len(list)#求均值
sum=0
for i in range(len(list)):
sum+=(list[i]-avg)**2
var=sum/len(list)# 求方差
probability=np.exp(-(v - avg) ** 2 / (2 * var** 2)) / (math.sqrt(2 * math.pi) * var)
return probability
调用模型进行训练
X,Y=prepare_data(df)
train_size = int(len(X) * 0.8)#划分训练集与测试集
X_train = np.array(X[:train_size])
print(X_train.shape)
Y_train=np.array(Y[:train_size])
Y_train.resize([Y_train.shape[0],1])
print(X_train[0][0])
print(Y_train[2][0])
X_test = np.array(X[train_size:])
Y_test =np.array( Y[train_size:])
Y_test.resize([Y_test.shape[0],1])
model=Bayes(X_train,Y_train,X_test,Y_test)
print(model.predict())
参考:
《统计学习方法》 李航
知乎文章 理解朴素贝叶斯分类的拉普拉斯平滑
https://zhuanlan.zhihu.com/p/26329951