【统计学习方法】感知机

一、前言

感知机是Frank Rosenblatt在1957年就职于康奈尔航空实验室时所发明的一种人工神经网络。它可以被视为一种最简单的前馈神经网络，是一种二元线性分类器。See more details in wikipdia感知机.
本篇blog将从统计学习方法三要素即模型、策略、算法三个方面介绍感知机，并给出相应代码实现。

二、模型

假设输入空间是$x\in R^n$，输出空间是$y\in \{-1,+1\}$，输入$x\in X$代表输入实例的特征向量，$y\in Y$对应于输入向量所属的类别。输入空间到输入空间的函数f(x)称为感知机，其中sign为指示函数，当输入为小于零的实数时，函数输出为+1，输入为大于零的实数时，函数输出为-1：
$$f(x)=sign(w\cdot x+b)$$
对应于特征空间$R^n$上的一个将其一分为二的超平面，w为其斜率，b为其截距，这个超平面的两侧对应于两个不同类别的向量，因此这个超平面又被称之为分离超平面。

三、策略

从感知机的数学模型及其几何解释可以显然看出，感知机在特征空间所生成的分离超平面可以对特征空间中的向量进行分类，对于给定数据集中的一个特定样本而言，若这个超平面将其错误分类（其所在超平面的一侧与其真实类别不对应），那么$y_i$与$w\cdot x_i+b$异号，即存在数学关系：
$$-y_i(w\cdot x_i+b)>0$$
由输入空间中任一点到分离超平面的距离公式可得到一个误分类点$x_i$到该分离超平面的距离为：
$$\frac{1}{||w||}\cdot y_i\cdot (w\cdot x_i+b)$$
对于给定数据集中所有误分类点（M为所有误分类点的集合），它们到该超平面的距离总和为：
$$-\frac{1}{||w||}\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$
不考虑$\frac{1}{||w||}$，则得到感知机学习所需的损失函数。
$$loss=\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$

四、算法

由上可知感知机算法是由误分类驱动的，具体采用随机梯度下降法来完成模型参数的学习。利用上述损失函数并分别对w和b求偏导可以得到

$${\nabla }_{w}L(w,b)=-\sum _{x_i\in M}{y}_i\cdot x_i$$

$${\nabla }_{b}L(w,b)=-\sum _{x_i\in M}{y}_i$$
对于随机选取的一个误分类点，设定学习率$\eta \in [0,1]$，w和b二者的更新方式如下：
$$w\leftarrow w+\eta y_i{x}_i$$
$$b\leftarrow b+\eta y_i$$
如此通过迭代更新，可以看到损失不断减小直至稳定在一定数值。故可以得到如下算法，亦感知机算法的原始形式：

4.1数据准备

方便起见，这里使用的数据将由sklearn.datasets中的make_blobs()函数生成：

data, labels = make_blobs(n_samples=500, n_features=5, centers=2)

将数据放入pandas的DataFrame中，观察如下（注意将labels中的0替换为-1）：

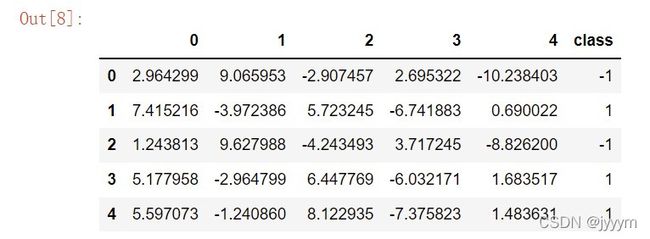
4.2 感知机学习算法的原始形式

1. 选取w和b的初值
2. 在训练集中随机选择一个样本及其对应的标签
3. 如果$y_i(w\cdot x_i+b)\le 0$则使用上述公式对w和b进行更新操作
4. 跳转至第(2)步，直到训练集中没有误分类点

4.2.1 感知机学习算法原始形式的收敛性

当训练数据集线性可分时，感知机学习算法原始形式迭代是收敛的，证明可见统计学习方法第42页至43页，或者Convergence Proof for the Perceptron Algorithm.

同时，感知机学习算法存在多解，这些解依赖于初值的选择和迭代过程中误分类点的选择顺序，若要得到唯一的分离超平面，需要对分离超平面增加约束条件。当训练集线性不可分时，感知机学习算法不收敛，迭代结果会发生震荡。

4.2.2 代码实现

根据感知机学习算法的原始形式，相应的Python实现如下：

class perceptron:
    #原始形式
    def __init__(self, lr, max_iter, feature_nums):
        rng = np.random.default_rng(42)
        self.lr = lr
        self.max_iter = max_iter
        self.coefs = rng.standard_normal(feature_nums) 
        self.intercept = rng.standard_normal(1)
        
    def sign(self, result):
        return 1 if result>0 else -1

    def upgrade(self, i, data, labels):
        w = self.coefs + self.lr * labels[i] * data[i]
        b = self.intercept + self.lr * labels[i]
        return w, b
    
    def fit(self, data, labels):
        for i in range(self.max_iter):
            while(True):
                index = np.random.choice(len(data))
                temp = labels[index] * (np.dot(self.coefs, data[index]) + self.intercept)
                if temp <= 0:
                    self.coefs, self.intercept = self.upgrade(index, data, labels)
                else:
                    break
        return self.coefs, self.intercept
    
    def predict(self, data):
        result = []
        for i in data:
            result.append(sign(self.intercept + np.dot(self.coefs, i)))
        return result
    
    def acc(self, y_pred, y_true):
        return sum(y_pred == y_true) / len(y_true)

4.3 感知机学习算法的对偶形式

从感知机学习算法的原始形式参数更新过程不难看出：最后模型学习到的参数w和b可以分别表示为：
$$w=\sum _{i=1}^N{a}_i{y}_i{x}_i$$
$$b=\sum _{i=1}^N{a}_i{y}_i$$
上式中N表示线性可分训练集中的样本总数，$a_i=n_i\eta$，$\eta$为学习率，故而感知机模型可以写作$f(x)=sign(\sum _{j=1}^N{a}_j{y}_j{x}_j\cdot x+b)$，其中$a=(a_1,a_2,...,a_N{)}^T$，感知机学习算法的对偶形式流程如下：

1. $a\leftarrow 0,b\leftarrow 0$
2. 在训练集中选择数据$(x_i,y_i)$
3. 如果存在$y_i(\sum _{j=1}^N{a}_j{y}_j{x}_j\cdot x_i+b)\le 0$则对参数进行更新：$a_i\leftarrow a_i+\eta$，$b\leftarrow b+\eta y_i$
4. 跳转至第二步直到没有误分类点。

对偶形式中的训练实例仅以内积形式存在，为了方便可以将训练集中实例间的内积计算出来并以矩阵的形式存储，这个矩阵就是Gram矩阵：
$$G=[x_i,x_j{]}_{NxN}$$

4.3.3 代码实现

根据感知机学习算法的对偶形式，相应的Python实现如下：

lr = 1
max_iter = 100
data = np.array([[3,3], [4,3], [1,1]])
labels = np.array([1,1,-1])

def gram(data):
    gram_matrix = np.zeros([len(data), len(data)])
    for i in range(len(data)):
        for j in range(len(data)):
            gram_matrix[i, j] = np.dot(data[i], data[j])
    return gram_matrix

def sign(result):
    return 1 if result>0 else -1
    
def init():
    a = np.zeros(len(data))
    b = 0
    return a, b

def train(data, label):
    a,b = init()
    for i in range(max_iter):
        while(True):
            index = np.random.choice(len(data))
            g = gram(data)
            temp = 0

            for j in range(len(data)):
                temp = temp + a[j] * label[j] * g[j, index]

            if label[index] * (temp + b) <=0:
                a[index] = a[index] + lr
                b = b + lr*label[index]
            else:
                break
            
    w = np.zeros(len(data[0]))
    for i in range(len(data)):
        w = a[i] * label[i] * data[i]
    return w, b

def predict(data, w, b):
    pred = []
    for i in data:
        pred.append(sign(np.dot(w, i) + b))
    return pred

这里为了简单起见，使用统计学习方法书上第45页例题的数据作为训练数据。