聚类分析数学建模

聚类分析基础入门与实践

概述

什么是聚类分析

1. 聚类是一个将数据集分为若干组（class）或类（cluster）的过程，并使得同一个组内的数据对象具有较高的相似度；而不同组中的数据对象是不相似的。
2. 相似或不相似是基于数据描述属性的取值来确定的，通常利用各数据对象间的距离来进行表示。
3. 聚类分析尤其适合用来讨论样本间的相互关联关系从而对一个样本结构做一个初步的评价。

例1：

​ 表中给出9个顾客的购买信息，包括购买的商品的数量及价格，根据此两个特征量，将顾客聚类成3类（购买大量的高价产品；购买少量的高价产品；购买少量的低价产品）。

	商品的数量	价格
	2	1700
类1	3	2000
	4	2300
	10	1800
类2	12	2100
	11	2500
	2	100
类3	3	200
	3	350

​ 聚类是一个非常困难的事情，因为在一个n维样本空间中，数据可以以不同的形状和大小揭示类。

​ 如在二维欧几里得空间中，上面的数据可以分为三个类，也可以分为4个类，类的数量的任意性是聚类过程中的主要问题。

聚类与分类的区别

• 聚类：没有具体的标准，没有参考数据。
• 分类：有具体的分类标准。

聚类分析的应用

• 市场分析：帮助市场分析人员从客户基本库中发现不同的客户群，并用购买模式刻画不同的客户群的特征
• 万维网：为WEB日志的数据进行聚类，以发现相同的用户访问模式
• 图像处理、模式识别、孤立点检测

什么是好的聚类

• 一个好的聚类方法将产生以下的高聚类
  • 最大化类内的相似性
  • 最小化类间的相似性
• 聚类结果的质量依靠所使用度量的相似性和它的执行
• 聚类方法的质量也可以用它发现一些或所有隐含模式的能力来度量

聚类的分类

​ 聚类分析有两种：一种是对样品的分类，称为Q型，另一种是对变量（指标）的分类，称为R型。

• R型聚类分析的主要作用：
  • 不但可以了解个别变量之间的亲疏程度，而且可以了解各个变量组合之间的亲疏程度。
  • 根据变量的分类结果以及他们之间的关系，可以选择主要变量进行Q型聚类分析或回归分析
• Q型聚类分析的主要作用：
  • 可以综合利用多个变量的信息对样本进行分析
  • 分类结果直观，聚类谱系图清楚地表现数值分类结果
  • 聚类分析所得到的结果比传统分类方法更细致、全面、合理

样品之间的相似度量——距离

常用的距离定义

​ 设有n个样品的p元观测数据：
$$x_{\text{i}}=(x_{\text{i1}},x_{\text{i2}},\cdots ,x_{\text{ip}}{)}^{\text{T}},\text{i}=1,2,\cdots ,\text{n}$$
​ 这时，每个样品可看成p元空间的一个点，每两个点之间的距离记为$d(x_{\text{i}},x_{\text{j}})$满足条件：
$$\begin{array}{rl}& d(x_{\text{i}},x_{\text{j}})\ge 0,且d(x_{\text{i}},x_{\text{j}})=0当且仅当x_{\text{i}}=x_{\text{j}}\\ & d(x_{\text{i}},x_{\text{j}})=d(x_{\text{j}},x_{\text{i}})\\ & d(x_{\text{i}},x_{\text{j}})\le d(x_{\text{i}},x_{\text{k}})+d(x_{\text{k}},x_{\text{j}})\end{array}$$

欧式距离：
$$d(x_{\text{i}},x_{\text{j}})={\left[\sum _{\text{k}=1}^{\text{p}}(x_{\text{ik}}-x_{\text{jk}}{)}^2\right]}^{\frac{1}{2}}$$
绝对距离：
$$d(x_{\text{i}},x_{\text{j}})=\sum _{\text{k}=1}^{\text{p}}|x_{\text{ik}}-x_{\text{jk}}|$$

明氏距离：
$$d(x_{\text{i}},x_{\text{j}})={\left[\sum _{\mathrm{k}=1}^{\text{p}}|x_{\mathrm{i}\mathrm{k}}-x_{\mathrm{j}\mathrm{k}}{|}^{\text{m}}\right]}^{\frac{1}{\text{m}}}$$
切氏距离：
$$d(x_{\text{i}},x_{\text{j}})=\underset{1\le \mathrm{k}\le \mathrm{p}}{\max }|x_{\mathrm{i}\mathrm{k}}-x_{\mathrm{j}\mathrm{k}}|$$
方差加权距离：
$$d(x_{\text{i}},x_{\text{j}})={\left[\sum _{\text{k}=1}^{\text{p}}(x_{\text{ik}}-x_{\text{jk}}{)}^2/{\text{s}}_{\text{k}}^2\right]}^{\frac{1}{2}}$$
马氏距离：
$$d(x_{\text{i}},x_{\text{j}})=\sqrt{(x_{\text{i}}-x_{\text{j}}{)}^{\text{T}}\sum {}^{-1}(x_{\text{i}}-x_{\text{j}})}$$
​ 式中$\sum {}^{-1}$为向量$x$和向量$y$的协方差矩阵的逆矩阵。

兰氏距离：
$$d(x_{\text{i}},x_{\text{j}})=\frac{1}{\text{p}}\sum _{\mathrm{k}=1}^{\text{p}}\frac{|x_{\text{ik}}-x_{\text{jk}}|}{x_{\text{ik}}+x_{\text{jk}}}$$
杰式距离：
$$d(x_{\text{i}},x_{\text{j}})={\left[\sum _{\text{k}=1}^{\text{p}}(\sqrt{x_{\text{ik}}}-\sqrt{x_{\text{jk}}}{)}^2\right]}^{\frac{1}{2}}$$
例2：

​ 13个国家1990,1995,2000可持续发展能力如下：分成4类

序号	国家	1990	1995	2000
1	澳大利亚	1249.39	1273.61	1282.68
2	巴西	821.6	859.85	919.73
3	加拿大	1641.01	1591.54	1608.32
4	中国	1330.45	1382.68	146.08
5	法国	1546.55	1501.77	1525.95
6	德国	1656.52	1630.52	1570.69
7	印度	861.30	862.51	945.11
8	意大利	1321.77	1232.3	1243.51
9	日本	1873.68	1949.89	1851.20
10	俄罗斯	1475.16	1315.87	1297
11	南非	794.25	787.48	782.38
12	英国	1486.75	1441.71	1465.12
13	美国	2824.29	2659.64	2740.12

采用不同的距离，得到的结果如下：

类别	欧式距离（最短距离）
1	日本
2	澳大利亚、加拿大、英、德、意、中、俄、法
3	巴西、印度、南非
4	美国

类别	欧式距离（ward距离）
1	澳大利亚、中、意、俄
2	加拿大、英、德、法、日本
3	巴西、印度、南非
4	美国

类别	马氏距离（ward距离）
1	日本
2	澳大利亚、加拿大、英、德、意、南非、俄、法
3	巴西、印度、中国
4	美国

​ 采用不同的距离计算公式，得到的分类也是不相同的。

变量间的相似度量——相似系数

​ 当对p个指标进行聚类时，用相似系数来衡量变量之间的相似程度（关联度），若用${\text{C}}_{\alpha ,\beta }$表示变量之间的相似系数，则应满足：
$$\begin{array}{rl}& |{\text{C}}_{\alpha ,\beta }|\le 1,且{\text{C}}_{\alpha ,\alpha }=1\\ & {\text{C}}_{\alpha ,\beta }=\pm 1,当且仅当\alpha =\text{k}\beta ,\text{k}\ne 0\\ & {\text{C}}_{\alpha ,\beta }={\text{C}}_{\beta ,\alpha }\end{array}$$
​ 相似系数中最常用的是相关系数与夹角余弦。

1. 夹角余弦

$${\text{C}}_{\mathrm{i},\mathrm{j}}(1)=\cos {\alpha }_{\mathrm{i}\mathrm{j}}=\frac{\sum _{\text{t}=1}^{\text{n}}{x}_{\mathrm{t}\mathrm{i}}{x}_{\mathrm{t}\mathrm{j}}}{\sqrt{\sum _{\text{t}=1}^{\text{n}}{x}_{\mathrm{t}\mathrm{i}}^2}\sqrt{\sum _{\text{t}=1}^{\text{n}}{x}_{\mathrm{t}\mathrm{j}}^2}}$$

2. 相关系数

$${\text{C}}_{\mathrm{i},\mathrm{j}}(2)=\frac{\sum _{\mathrm{t}=1}^{\text{n}}(x_{\mathrm{t}\mathrm{i}}-{\overline{x}}_{\text{i}})(x_{\mathrm{t}\mathrm{j}}-{\overline{x}}_{\text{j}})}{\sqrt{\sum _{\mathrm{t}=1}^{\text{n}}(x_{\mathrm{t}\mathrm{i}}-{\overline{x}}_{\text{i}}{)}^2}\sqrt{\sum _{\mathrm{t}=1}^{\text{n}}(x_{\mathrm{t}\mathrm{j}}-{\overline{x}}_{\text{j}}{)}^2}}$$

类间距离

​ 前面，我们介绍了两个向量之间的距离，下面我们介绍两个类别之间的距离：

​ 设$d{}_{\mathrm{i}\mathrm{j}}$表示；两个样品$x_{\text{i}},x_{\text{j}}$之间的距离，${\mathrm{G}}_{\mathrm{p}},{\mathrm{G}}_{\mathrm{q}}$分别表示两个类别，各自含有${\mathrm{n}}_{\mathrm{p}},{\mathrm{n}}_{\mathrm{q}}$个样品。

• 最短距离：

$$D_{\mathrm{p}\mathrm{q}}=\underset{\mathrm{i}\in {\mathrm{G}}_{\mathrm{p}},\mathrm{j}\in {\mathrm{G}}_{\mathrm{q}}}{\min }{d}_{\mathrm{i}\mathrm{j}}$$

​ 即用两类中样品之间的距离最短者作为两类间距离。

• 最长距离：

$$D_{\mathrm{p}\mathrm{q}}=\underset{\mathrm{i}\in {\mathrm{G}}_{\mathrm{p}},\mathrm{j}\in {\mathrm{G}}_{\mathrm{q}}}{\max }{d}_{\mathrm{i}\mathrm{j}}$$

​ 即用两类中样品之间的距离最长者作为两类间距离。

• 类平均距离：

$$D_{\mathrm{p}\mathrm{q}}=\frac{1}{{\mathrm{n}}_{\mathrm{p}}{\mathrm{n}}_{\mathrm{q}}}\sum _{\mathrm{i}\in {\mathrm{G}}_{\mathrm{p}}}\sum _{\mathrm{j}\in {\mathrm{G}}_{\mathrm{q}}}{d}_{\mathrm{i}\mathrm{j}}$$

​ 即用两类中所有两两样品之间的距离的平均作为两类间的距离

• 重心距离：

$$D_{\mathrm{p}\mathrm{q}}=d({\overline{x}}_{\text{p}},{\overline{x}}_{\text{q}})=\sqrt{({\overline{x}}_{\text{p}}-{\overline{x}}_{\text{q}}{)}^{\text{T}}({\overline{x}}_{\text{p}}-{\overline{x}}_{\text{q}})}$$

​ 其中${\overline{x}}_{\text{p}},{\overline{x}}_{\text{q}}$分别是${\mathrm{G}}_{\mathrm{p}},{\mathrm{G}}_{\mathrm{q}}$的重心，这是用两类的重心之间的欧式距离作为两类间的距离。（类G的样本x有p个不同的属性，所以类的样本是一个向量）

• 离差平方和距离（ward）：

$$D_{\mathrm{p}\mathrm{q}}^2=\frac{{\mathrm{n}}_{\mathrm{p}}{\mathrm{n}}_{\mathrm{q}}}{{\mathrm{n}}_{\mathrm{p}}+{\mathrm{n}}_{\mathrm{q}}}({\overline{x}}_{\text{p}}-{\overline{x}}_{\text{q}}{)}^{\text{T}}({\overline{x}}_{\text{p}}-{\overline{x}}_{\text{q}})$$

​ 显然，离差平方和距离与重心距离的平方成正比。

谱系聚类法的步骤

基本思想

1. 选择样本间距离的定义及类间距离的定义；
2. 计算n个样本两两之间的距离，得到距离矩阵$D=(d_{\mathrm{i}\mathrm{j}})$；
3. 构造个类，每类只含有一个样本；
4. 合并符合类间距离定义要求的两类为一个新类；
5. 计算新类与当前各类的距离。若类的个数为1，则转到步骤6，否则回到步骤4；
6. 画出聚类图；
7. 决定类的个数和类；

步骤

1. n个样品开始作为n个类，计算两两之间的距离或相似系数，得到实对称矩阵：

$${\mathbf{D}}_0=\left[\begin{array}{cccc}{d}_{11}& d_{12}& \cdots & d_{1\mathrm{n}}\\ d_{21}& d_{22}& \cdots & d_{2\mathrm{n}}\\ ⋮& ⋮& \ddots & ⋮\\ d_{\mathrm{n}1}& d_{\mathrm{n}2}& \cdots & d_{\mathrm{n}\mathrm{n}}\end{array}\right]$$

2. 从D₀的非主对角线先上找到最小（距离）或最大元素（相似系数），设该元素是${\text{D}}_{\mathrm{p}\mathrm{q}}$，则将${\mathrm{G}}_{\mathrm{p}},{\mathrm{G}}_{\mathrm{q}}$合并成一个新类${\mathrm{G}}_{\mathrm{r}}=\{{\mathrm{G}}_{\mathrm{p}},{\mathrm{G}}_{\mathrm{q}}\}$，在${\text{D}}_0$中去掉${\mathrm{G}}_{\mathrm{p}},{\mathrm{G}}_{\mathrm{q}}$所在的两行、两列，并加上新类与其余各类之间的距离（或相似系数），得到n-1阶矩阵${\mathrm{D}}_1$。
3. 从${\mathrm{D}}_1$出发重复步骤$(2)$的做法得到${\mathrm{D}}_2$，再由${\mathrm{D}}_2$出发重复上述步骤，直到所有样品聚为一个大类为止。
4. 在合并过程中记下合并样品的编号及两类合并时的水平，并绘制聚类谱系图。

例3

​ 为了研究辽宁等5省1991年城镇居民生活消费情况的分布规律，根据调查资料做类型分类，用最短距离做类间分类。数据如下：

	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$x_7$	$x_8$
辽宁1	7.90	39.77	8.49	12.94	19.27	11.05	2.04	13.29
浙江2	7.68	50.37	11.35	13.30	19.25	14.59	2.75	13.29
河南3	9.42	27.93	8.20	8.14	16.17	9.42	1.55	14.87
甘肃4	9.16	27.98	9.01	9.32	15.99	9.10	1.82	9.76
青海5	10.06	28.64	10.52	10.05	16.18	8.39	1.96	10.82

​ 将每一个省区视为一个样品，先计算5个省区之间的欧氏距离，用${\mathrm{D}}_0$表示距离矩阵（对称矩阵，固给出下三角阵）。
$${\text{D}}_0=\left[\begin{array}{ccccc}0& & & & \\ 11.67& 0& & & \\ 13.80& 24.63& 0& & \\ 13.12& 24.06& 2.20& 0& \\ 12.80& 23.54& 3.51& 2.21& 0\end{array}\right]$$
​ ${\text{D}}_0$中最小元素为${\text{D}}_0(4,3)$，也就是甘肃和河南之间的欧式距离最小，所以我们将3（河南）和4（甘肃）合并为一类，为类6，代替了3、4两类。类6与剩余的1、2、5之间的距离分别为：
$$\begin{array}{rl}& d(3.4{)}_1=\min (d_{31},d_{41})=\min (13.80,13.12)=13.12\\ & d(3.4{)}_2=\min (d_{32},d_{42})=\min (24.63,24.06)=24.06\\ & d(3.4{)}_5=\min (d_{52},d_{52})=\min (3.51,2.21)=2.21\end{array}$$
​ 得到新矩阵${\text{D}}_1$：
$${\text{D}}_1=\left[\begin{array}{cccc}0& & & \\ 13.12& 0& & \\ 24.06& 11.67& 0& \\ 2.21& 12.08& 23.54& 0\end{array}\right]$$
​ 最小元素为2.21，合并类6和类5，得到类7。类7与剩余的1、2之间的距离分别为：
$$\begin{array}{rl}& d(5,6{)}_1=\min (d_{51},d_{61})=\min (12.80,13.12)=12.08\\ & d(5,6{)}_2=\min (d_{52},d_{62})=\min (23.54,24.06)=23.54\end{array}$$
​ 得到新矩阵：
$${\text{D}}_2=\left[\begin{array}{ccc}0& & \\ 12.08& 0& \\ 23.54& 11.67& 0\end{array}\right]$$
​ 最小元素为11.67，合并类1和类2，得到类8，此时我们有两个不同的类，他们的最近距离：
$$\begin{array}{rl}& d(7,8)=\min (d_{71},d_{72})=\min (12.80,23.54)=12.08\end{array}$$
​ 得到新矩阵：
$${\text{D}}_3=\left[\begin{array}{cc}0& \\ 12.08& 0\end{array}\right]$$
​ 最后合并为一个大类。这就是按最短距离定义类间距离的系统聚类方法。最长距离法类似。

谱系聚类的MATLAB实现

1. 输入数据矩阵，注意行与列的实际意义

2. 计算各样品之间的距离

   1. 欧式距离：d=pdist(A);
   2. 绝对距离：d=pdist(A,'cityblock');
   3. 明氏距离：d=pdist(A,'minkowski',r)；%r要填上具体的实数
   4. 方差加权距离：d=pdist(A,'seclid');
   5. 马氏距离：d=pdist(A,'mahal');

   注意：以上命令输出的结果是一个行向量，如果要得到距离矩阵，可以用命令：D=squareform(d);

   若要得到下三角阵，可以用命令：k=tril(squareform(d))。

3. 选择不同的类间距离进行聚类

   1. 最短聚类：z=linkage(d);%此处及一下的d都是（2）中算出的距离行向量
   2. 最常距离：z=linkage(d,'complete');
   3. 中间距离：z=linkage(d,'centroid');
   4. 中心距离：z=linkage(d,'average');
   5. 离差平方和：z=linkage(d,'ward');

   注意：此时输出的结果是一个n-1行3列的矩阵（因为每次聚类的结果都是两个类合成一个类，所以是n-1阶），每一行表示在某水平上合并为一类的序号。

4. 作出谱系聚类图

   命令为：H=dendrogram(z,d);%注意若样本少于30，可以省去d，否则必须填写

5. 根据分类数目，输出聚类结果

   T=cluster(z,k);%注意k是分类数目，z是（3）中的结果

   find(T=k0);%找出属于第k0类的样品编号

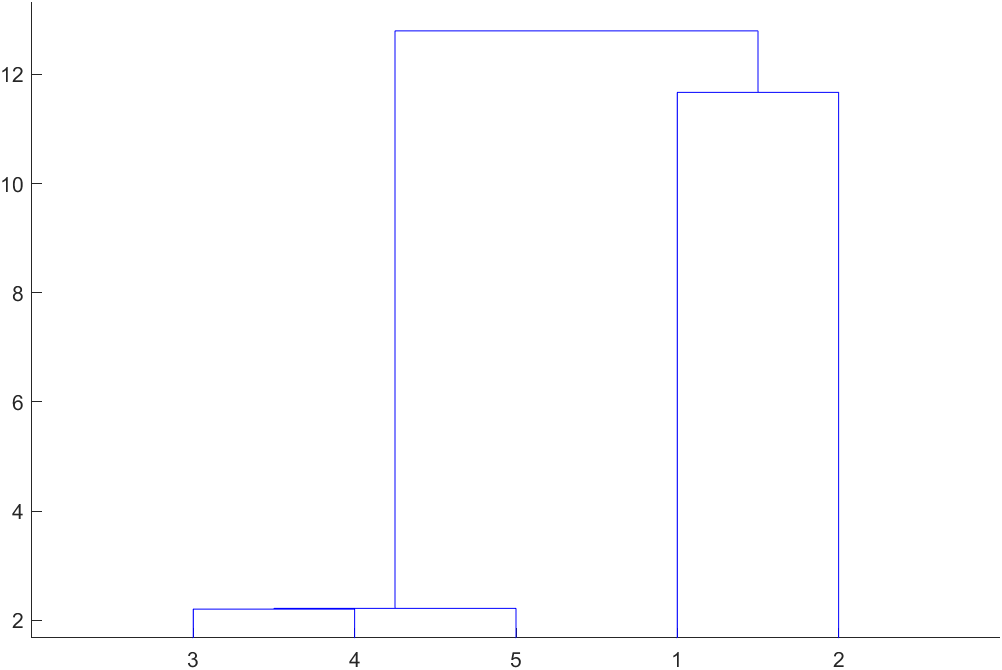
例4：将例3利用MATLAB软件进行聚类

1. 输入数据矩阵：

b =

    7.9000   39.7700    8.4900   12.9400   19.2700   11.0500    2.0400   13.2900
    7.6800   50.3700   11.3500   13.3000   19.2500   14.5900    2.7500   14.8700
    9.4200   27.9300    8.2000    8.1400   16.1700    9.4200    1.5500    9.7600
    9.1600   27.9800    9.0100    9.3200   15.9900    9.1000    1.8200   11.3500
   10.0600   28.6400   10.5200   10.0500   16.1800    8.3900    1.9600   10.8100

2. 计算各样品之间的距离：

d=pdist(b);		%欧式距离

​ 输出结果为：

d =

   11.6726   13.8054   13.1278   12.7983   24.6353   24.0591   23.5389    2.2033    3.5037    2.2159

​ 共有是10个元素（${\text{C}}_5^2$），然后可以求出距离矩阵和三角矩阵：

D=squareform(d);	%距离矩阵
k=tril(D);		%三角矩阵

​ 得到的结果如下：

D =

         0   11.6726   13.8054   13.1278   12.7983
   11.6726         0   24.6353   24.0591   23.5389
   13.8054   24.6353         0    2.2033    3.5037
   13.1278   24.0591    2.2033         0    2.2159
   12.7983   23.5389    3.5037    2.2159         0
   
   k =

         0         0         0         0         0
   11.6726         0         0         0         0
   13.8054   24.6353         0         0         0
   13.1278   24.0591    2.2033         0         0
   12.7983   23.5389    3.5037    2.2159         0

3. 选择不同的类间距离进行聚类：

z=linkage(d);	%通过最短距离进行聚类

​ 输出结果为：

z =

    3.0000    4.0000    2.2033
    5.0000    6.0000    2.2159
    1.0000    2.0000   11.6726
    7.0000    8.0000   12.7983

• 在2.2033的水平，${\mathrm{G}}_3,{\mathrm{G}}_4$合成一类为${\mathrm{G}}_6$；
• 在2.2159的水平，${\mathrm{G}}_6,{\mathrm{G}}_5$合成一类为${\mathrm{G}}_7$；
• 在11.6726的水平，${\mathrm{G}}_1,{\mathrm{G}}_2$合成一类为${\mathrm{G}}_8$；
• 在2.2033的水平，${\mathrm{G}}_7,{\mathrm{G}}_8$合成一类。

4. 作出谱系图

H=dendrogram(z);

最短距离聚类图

5. 输出聚类结果

T=cluster(z,3);		%分为3类

​ 输出结果如下：

T =

     1
     2
     3
     3
     3

​ 结果表明：若分为三类，则辽宁是一类，浙江也是一类，河南、青海和甘肃是另一类。

​ 我们可以找出第三类的样品编号：

find(T==3)

​ 结果如下：

ans =

     3
     4
     5

​ 也就是河南、青海和甘肃分为一类。

K-平均聚类算法

介绍

• ​ K-平均（k-means）算法以k为参数，把n个对象分为k个簇，以使簇内对象具有较高的相似对，而簇间的相似度较低。
• 相似度的计算根据一个簇中对象的平均值（被看做簇的重心）来进行。

算法的基本思想

1. 首先，随机的选择k个对象，每个对象初始的代表了一个簇的平均值；（也就是初始化k个重心）
2. 对剩余的每个对象，根据其余各个簇中心的距离，将它分给最近的重心；
3. 然后重新计算每个簇的平均值。
4. 这个过程不断重复，直到准则函数收敛（或者结果不再变化）。

​ 通常选择方差作为收敛准则函数：
$$\text{E}=\sum _{\mathrm{i}=1}^{\text{m}}\sum _{\mathrm{p}\in {\mathrm{C}}_{\mathrm{i}}}|\mathrm{p}-{\mathrm{m}}_{\mathrm{i}}{|}^2$$
​ 其中E为数据库中所有对象的均方值之和；p为代表对象的空间中的一个点；m_i为聚类C_i的均值（p和m_i均是多维的）。

​ 这个准则试图使得生成的结果尽可能地紧凑和独立；当结果簇是密集的，且簇与簇之间区别明显时，算法的效果较好。

算法的特点

• 只适用于聚类均值有意义的场合，在某些应用中，如：数据集中包含符号属性时，直接应用k-means算法就有问题；
• 用户必须事先指定k的个数；
• 对噪声和孤立点数据敏感，少量的该类数据能够对聚类均值起到很大影响。