【深度学习基础】学习率(learning rate)的理解与分类

1. 训练与学习率的关系

首先介绍一下训练过程，这样便于我们对超参数和学习率的理解。反向传播可分为四部分，分别是前向传导、损失函数、后向传导，以及权重更新。

在第一次训练的时候，权重或者过滤器值都是随机初始化的，输出可能为[.1 .1 .1 .1 .1 .1 .1 .1 .1 .1]，即一个不偏向任何数字的输出。

接下来是反向传播的损失函数部分。损失函数的定义方式有许多种方法，常见的一种是MSE(均方误差)

$$E_{total}={\sum }_{}\frac{1}{2}(target-output{)}^2$$
现在假设L等同于上面的数值，为了使得训练的结果与训练的标记结果相同，就要使损失数值L最小化，也就是说我们要找出来哪一部分的输入(权重)直接导致了网络的损失(或错误)，然后进行反向传播：

学习速率是一个由程序员决定的参数。高学习速率意味着权重更新的动作更大，因此可能该模式将花费更少的时间收敛到最优权重。然而，学习速率过高会导致跳动过大，不够准确以致于达不到最优点。

总的来说，前向传导、损失函数、后向传导、以及参数更新被称为一个学习周期。对每一训练图片，程序将重复固定数目的周期过程。一旦完成了最后训练样本上的参数更新，网络有望得到足够好的训练，以便层级中的权重得到正确调整。

那么我们怎么知道要用多少层、多少卷积层、过滤器尺寸是多少、以及步幅和填充值多大呢？这些问题很重要，但又没有一个所有研究人员都在使用的固定标准。这是因为神经网络很大程度上取决于你的数据类型。图像的大小、复杂度、图像处理任务的类型以及其他更多特征的不同都会造成数据的不同。对于你的数据集，想出如何选择超参数的一个方法是找到能创造出图像在合适尺度上抽象的正确组合。

神经网路中的超参数主要包括:

1. 学习率 η
2. 正则化参数 λ
3. 神经网络的层数 L
4. 每一个隐层中神经元的个数 j
5. 学习的回合数Epoch
6. 小批量数据 minibatch的大小
7. 输出神经元的编码方式
8. 代价函数的选择
9. 权重初始化的方法
10. 神经元激活函数的种类
11. 参加训练模型数据的规模 。
12. 其他参数：冲量。。。等等

这些都是可以影响神经网络学习速度和最后分类结果，其中神经网络的学习速度主要根据训练集上代价函数下降的快慢有关，而最后的分类的结果主要跟在验证集上的分类正确率有关。因此可以根据该参数主要影响代价函数还是影响分类正确率进行分类。

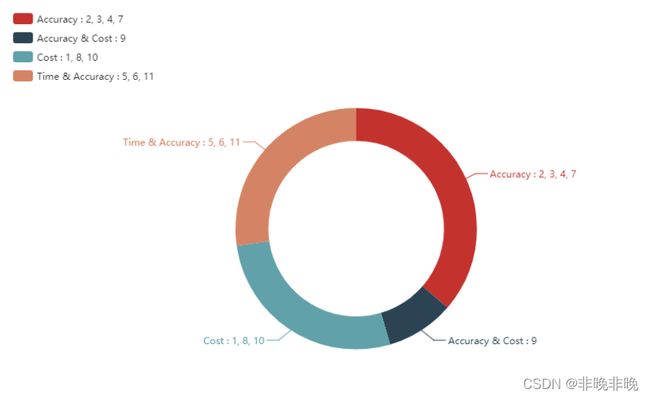
在上图中可以看到超参数 2，3，4， 7 主要影响的时神经网络的分类正确率；9 主要影响代价函数曲线下降速度，同时有时也会影响正确率；1，8，10 主要影响学习速度，这点主要体现在训练数据代价函数曲线的下降速度上；5，6，11 主要影响模型分类正确率和训练用总体时间。这上面所提到的是某个超参数对于神经网络想到的首要影响，并不代表着该超参数只影响学习速度或者正确率。

通常学习率有以下几种：

改变学习率	优化算法
固定衰减	分段常数衰减、逆时衰减、 （自然）指数衰减、余弦衰减
周期变化	循环学习率、SGDR
自适应	Adagrad、RMSporp、AdaDeltea

2. 学习率的衰减策略

​ 在模型优化中，常用到的几种学习率衰减方法有：分段常数衰减、多项式衰减、指数衰减、自然指数衰减、余弦衰减、线性余弦衰减、噪声线性余弦衰减。便于理解，先来看看学习率涉及的一些概念，如下表所示：

参数名称	参数说明
learning_rate	初始学习率
global_step	用于衰减计算的全局步数，非负，用于逐步计算衰减指数
decay_steps	衰减步数，必须是正值，决定衰减周期
decay_rate	衰减率
end_learning_rate	最低的最终学习率
cycle	学习率下降后是否重新上升
alpha	最小学习率
num_periods	衰减余弦部分的周期数
initial_variance	噪声的初始方差
variance_decay	衰减噪声的方差

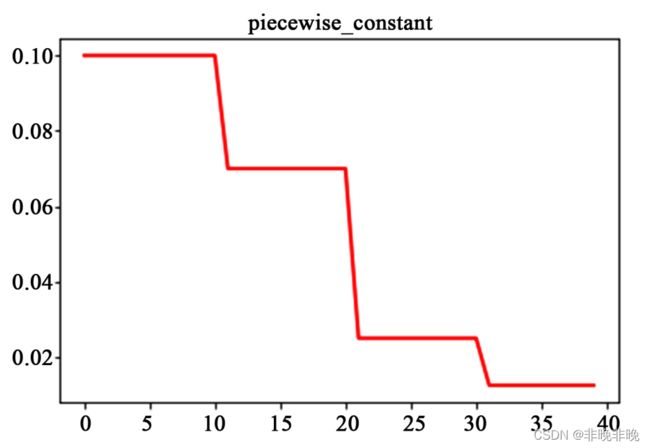
（1）分段常数衰减

分段常数衰减需要事先定义好的训练次数区间，在对应区间置不同的学习率的常数值，一般情况刚开始的学习率要大一些，之后要越来越小，要根据样本量的大小设置区间的间隔大小，样本量越大，区间间隔要小一点。下图即为分段常数衰减的学习率变化图，横坐标代表训练次数，纵坐标代表学习率。

（2）指数衰减

以指数衰减方式进行学习率的更新，学习率的大小和训练次数指数相关，其更新规则为：

$$decayed\_learning\_rate=learning\_rate\ast decay\_rat{e}^{\frac{global\_step}{decay\_steps}}$$

这种衰减方式简单直接，收敛速度快，是最常用的学习率衰减方式，如下图所示，绿色的为学习率随训练次数的指数衰减方式，红色的即为分段常数衰减，它在一定的训练区间内保持学习率不变。

（3）自然指数衰减

它与指数衰减方式相似，不同的在于它的衰减底数是$e$，故而其收敛的速度更快，一般用于相对比较容易训练的网络，便于较快的收敛，其更新规则如下：
$$decayed\_learning\_rate=learning\_rate\ast e^{\frac{-decay\_rate}{global\_step}}$$
下图为分段常数衰减、指数衰减、自然指数衰减三种方式的对比图，红色的即为分段常数衰减图，阶梯型曲线。蓝色线为指数衰减图，绿色即为自然指数衰减图，很明可以看到自然指数衰减方式下的学习率衰减程度要大于一般指数衰减方式，有助于更快的收敛。

（4）多项式衰减

应用多项式衰减的方式进行更新学习率，这里会给定初始学习率和最低学习率取值，然后将会按照给定的衰减方式将学习率从初始值衰减到最低值,其更新规则如所示：
$$global\_step=min(global\_step,decay\_steps)$$
$$\begin{gathered} decayed\_learning\_rate=(learning\_rate-end\_learning\_rate)\ast {\left(1-\frac{global\_step}{decay\_steps}\right)}^{power} \\ +end\_learning\_rate \end{gathered}$$
需要注意的是，有两个机制，降到最低学习率后，到训练结束可以一直使用最低学习率进行更新，另一个是再次将学习率调高，使用 decay_steps 的倍数，取第一个大于 global_steps 的结果，如下式所示.它是用来防止神经网络在训练的后期由于学习率过小而导致的网络一直在某个局部最小值附近震荡，这样可以通过在后期增大学习率跳出局部极小值。
$$decay\_steps=decay\_steps\ast ceil\left(\frac{global\_step}{decay\_steps}\right)$$
如下图所示，红色线代表学习率降低至最低后，一直保持学习率不变进行更新，绿色线代表学习率衰减到最低后，又会再次循环往复的升高降低。

（5）余弦衰减

余弦衰减就是采用余弦的相关方式进行学习率的衰减，衰减图和余弦函数相似。其更新机制如下式所示：
$$global\_step=min(global\_step,decay\_steps)$$

$$cosine\_decay=0.5\ast \left(1+cos\left(\pi \ast \frac{global\_step}{decay\_steps}\right)\right)$$

$$decayed=(1-\alpha )\ast cosine\_decay+\alpha$$

$$decayed\_learning\_rate=learning\_rate\ast decayed$$

如下图所示，红色即为标准的余弦衰减曲线，学习率从初始值下降到最低学习率后保持不变。蓝色的线是线性余弦衰减方式曲线，它是学习率从初始学习率以线性的方式下降到最低学习率值。绿色噪声线性余弦衰减方式。

（6）Lambda学习率

顾名思义，Lambda学习率就是自定义一个关于迭代次数的Lambda函数，Lambda函数形式如下图所示。

3. 周期性学习率

为了使得梯度下降方法能够逃离局部最小值或鞍点，一种经验性的方式是在训练过程中周期性地增大学习率。虽然增加学习率可能短期内有损网络的收敛稳定性，但从长期来看有助于找到更好的局部最优解。一般而言，当一个模型收敛一个平坦（Flat）的局部最小值时，其鲁棒性会更好，即微小的参数变动不会剧烈影响模型能力；而当模型收敛到一个尖锐（Sharp）的局部最小值时，其鲁棒性也会比较差。具备良好泛化能力的模型通常应该是鲁棒的，因此理想的局部最小值应该是平坦的。周期性学习率调整可以使得梯度下降方法在优化过程中跳出尖锐的局部极小值，虽然会短期内会损害优化过程，但最终会收敛到更加理想的局部极小值。下面介绍两种常用的周期性调整学习的方法。

（1）循环学习率

一种简单的方法是使用循环学习率（Cyclic Learning Rate），即在让学习率在一个区间内周期性地增大和缩小。通常可以使用线性缩放来调整学习率，称为三角循环学习率（Triangular Cyclic Learning Rate）。假设每个循环周期的长度相等都为$2∆T$，其中前$∆T $步为学习率线性增大阶段，后$∆T $步为学习率线性缩小阶段。在第t次迭代时，其所在的循环周期数m为：

第t次迭代的学习率为：

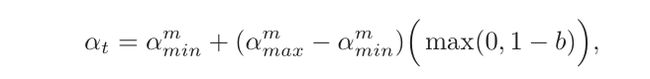
其中${\alpha }_{max},{\alpha }_{min}$分别为第m个周期中学习率的上界和下界，可以随着m的增大而逐渐降低；b ∈ [0,1]的计算为:

循环学习率论文：Accurate, large mini-batch sgd: Training imagenet in 1 hour，Goyal. et al., 2017

（2）带热重启的随机梯度下降

带热重启的随机梯度下降（Stochastic Gradient Descent with Warm Restarts，SGDR），是用热重启方式来替代学习率衰减的方法。学习率每间隔一定周期后重新初始化为某个预先设定值，然后逐渐衰减。每次重启后模型参数不是从头开始优化，而是从重启前的参数基础上继续优化。

假设在梯度下降过程中重启M次，第m次重启在上次重启开始第$T_m$个回合后进行，$T_m$称为重启周期。在第m次重启之前，采用余弦衰减来降低学习率。第t次迭代的学习率为：

其中${\alpha }_{max},{\alpha }_{min}$分别为第m个周期中学习率的上界和下界，可以随着m的增大而逐渐降低；$T_{cur}$ 为从上次重启之后的回合（Epoch）数。$T_{cur}$可以取小数，比如0.1,0.2等，这样可以在一个回合内部进行学习率衰减。重启周期$T_m$ 可以随着重启次数逐渐增加，比如$T_m=T_{m-1}\times \kappa$，其中κ ≥ 1为放大因子。

下图中，左边为三角循环学习率，右边为带热重启的余弦衰减。

4. 自适应学习率

（1）Adagrad算法

在Adagrad算法中，如果某个参数的偏导数累积比较大，其学习率相对较小；相反，如果其偏导数累积较小，其学习率相对较大。但整体是随着迭代次数的增加，学习率逐渐缩小。Adagrad算法的缺点是在经过一定次数的迭代依然没有找到最优点时，由于这时的学习率已经非常小，很难再继续找到最优点。

（2）RMSprop算法

RMSprop算法是Geoff Hinton提出的一种自适应学习率的方法[Tieleman and Hinton, 2012]，可以在有些情况下避免AdaGrad算法中学习率不断单调下降以至于过早衰减的缺点。RMSProp算法和Adagrad算法的区别在于$G_t$ 的计算由累积方式变成了指数衰减移动平均。在迭代过程中，每个参数的学习率并不是呈衰减趋势，既可以变小也可以变大。

（3）AdaDelta算法

AdaDelta算法[Zeiler, 2012]也是 Adagrad算法的一个改进。和RMSprop算法类似，AdaDelta算法通过梯度平方的指数衰减移动平均来调整学习率。此外，AdaDelta算法还引入了每次参数更新差$∆\theta$的平方的指数衰减权移动平均。

---

参考：
https://www.zhihu.com/question/52668301
https://blog.csdn.net/qq_36559293/article/details/103384257
超参数调整：
https://blog.csdn.net/dugudaibo/article/details/77366245?ops_request_misc=%7B%22request%5Fid%22%3A%22163927806416780261948300%22%2C%22scm%22%3A%2220140713.130102334..%22%7D&request_id=163927806416780261948300&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-2-77366245.first_rank_v2_pc_rank_v29&utm_term=神经网络参数&spm=1018.2226.3001.4187

参数：
https://blog.csdn.net/yudiemiaomiao/article/details/72391316?ops_request_misc=%7B%22request%5Fid%22%3A%22163927806416780261948300%22%2C%22scm%22%3A%2220140713.130102334..%22%7D&request_id=163927806416780261948300&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-3-72391316.first_rank_v2_pc_rank_v29&utm_term=神经网络参数&spm=1018.2226.3001.4187