细读informer与项目学习
文章目录
- 摘要
- 一. 细读informer
-
- 1.1 背景与回顾
-
- 1.1.1 Transformer类模型的Challenges以及形成的原因
- 1.1.2 如何改进与突破挑战?
- 1.2 informer模型的设计来源与理论支撑
-
- 1.2.1 衡量Query稀疏性
- 1.2.2 ProbSparse(probability sparse – 概率分布稀疏)自注意力的设计出现
- 1.2.3 encoder 处理长序列输入
- 1.2.4 Decoder输出提速
- 1.3 informer模型的总体架构
- 1.4 实验部分与结果分析
-
- 1.4.1 实验数据集与比较模型,以及评估指标
- 1.4.2 消融实验
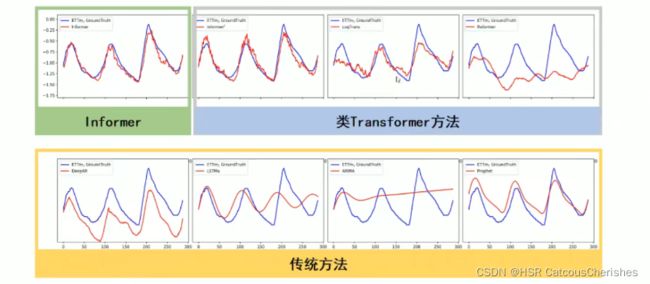
- 1.5 Informer模型的预测效果对比
- 二. 力源项目数据据库相关问题
-
- 2.1 产品二维码数据库表更新同步到云数据库
- 2.2 改进方案
- 2.3下一步具体实现自动同步
- 2.4 另:关于手机定位显示在web页面功能得实现
- 三. 深度学习基础知识
- 四.总结
摘要
本周一是再次细读上周informer模型中没有理解的点,以及重新回顾了informer的研究背景与类Transformer模型存在的三大挑战与形成的原因;对informer模型的设计来源与理论支撑有着进一步的理解,从衡量Query稀疏性,度量方法的建立,到probability sparse – 概率分布稀疏自注意力的设计出现,与如何具体计算实现ProbSparse self-attention。
二是在力源项目上的数据库同步更新问题的实现步骤与进一步优化探究;以及APP 端学习与APP端的生成导出。
一. 细读informer
1.1 背景与回顾
对于LSTF问题的预测研究,一直是一个重要研究方向。从LSTM只能做短期较为精准的预测,到Transformer在有限的算力下很难做到长期时序预测精准的问题。Transformer模型在时序预测有着比较好的性能(由于attention机制),但针对transformer类模型运用在LSTF上存在的三大问题;二次时间复杂度,高内存,encoder-decoder架构局限性;Informer随之设计相应的改进方案,即ProbSparse 自注意机制,自注意蒸馏操作,生成式解码器等关键创新点。
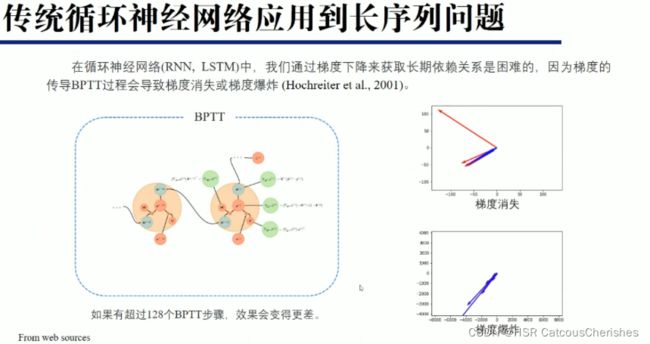
对于传统的循环神经网络在长序列问题上一般都不是很好的效果:比如传统的RNN-based模型不能够用于长时序预测问题。如下图,随着时序数据长度不断增加,LSTM预测速度迅速下降(红线),无法在规定时间和有限的计算能力下进行有效预测序列。另一方面,RNN-based误差不断累积,导致MSE指标(蓝线)迅速增加,作者认为序列长度大于48的预测结果属于无法使用的情况。
RNN-based模型还存在梯度消失和梯度爆炸的问题。
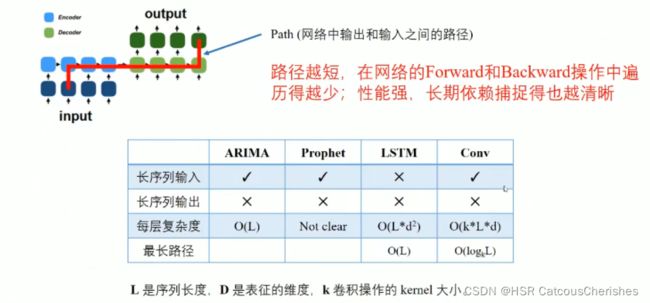
最关键的是路径问题,无法有效捕获依赖信息:
注意力机制的发展历程与研究:

在2017年之前的做法大致基本如下的研究改进:

Transformer自2017年提出之后大放异彩, 首先是encoder-decoder架构,以及self-attention机制兴起(具体怎么做之前笔记有所提及),并且由于self-attention的点乘机制,使得输入和输出可以直接交换信息,所以最长路径为 O ( 1 ) O(1) O(1)(如下图),可以捕获长时序的依赖关系,具有能够处理长时序预测问题的能力。然而,它另外三项指标都是不友好的。

Long sequence predicion 本文所研究的问题,关注的是LSTF的output的准确性,以及长序列预测中input的统一表征,建立一个Long sequence output 与 Long sequence input 之间的映射关系 。
1.1.1 Transformer类模型的Challenges以及形成的原因
(简单回顾)
1.每一层的计算复杂度为O(L2):自注意力中(原子操作)的点积运算,每一对Input都要做attention运算。
2. 对于Long Input的问题:Encoder-Decoder的layer堆叠导致内存开销出现瓶颈,层数J过多,导致复杂度进一步增大【计算复杂度为O(J*L2)】.
3. 对于Long Output的问题:预测长序列输出的速度会下降,因为原始的Transformer的decoder在inference的过程中是动态输出的,即上一次的Output是下一次的Input,进而和隐藏层一起再预测下一次的Output,使得Transformer的Inference过程和RNN一样慢。
1.1.2 如何改进与突破挑战?
- 解决思路:减低attention的计算量——ProbSparse self-attention

上图中是之前的对self-attention改进工作,都是固定方式的,没有可适应性;由于self-attention具有稀疏性,分布呈长尾分布,只有少数点积对主要注意力有贡献,其他点积只有非常微弱的作用,可以忽略。
1.2 informer模型的设计来源与理论支撑
关键点就是如何解决之前都存在的三个问题!
首先是之前提及过的做一个时序输入的统一表征(具体如何输入再看代码):

1.2.1 衡量Query稀疏性
作者从概率的角度看待自注意力,提出了衡量自注意力稀疏性的一种标准。
定义一个概率的形式 如下:

即在给定第i个query的条件下key的分布。
如果这个概率分布接近了均匀分布:
![[公式]](http://img.e-com-net.com/image/info8/9d8983fa92b94453a415f19d4b45bcb3.jpg)
那就说明这个query是“Lazy”的,没法选出重要的那些key,反之就说明该query是“active”的。
![]()
由于active的query对自注意力贡献很大,而lazy的query贡献很小,所以我们尽可能的选出那些active的query。
从这个角度出发,用KL散度衡量 p ( k j ∣ q i ) p(k_j|q_i) p(kj∣qi)和 q ( k j ∣ q i ) q(k_j|q_i) q(kj∣qi)的相似性,从而衡量query的稀疏性。
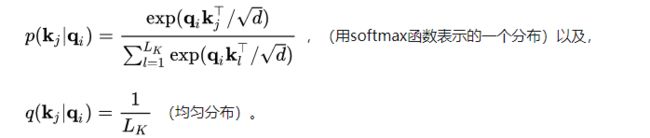

KL散度公式推导过程大致如下:

得到,第i个query的“稀疏度度量”,该值越大,说明概率分布和均匀分布差异越大,该query越活跃,得到了一个衡量query的标准。
1.2.2 ProbSparse(probability sparse – 概率分布稀疏)自注意力的设计出现
上面的 Q − Q^- Q− 是一个稀疏矩阵,采用上述的衡量标准,论文作者用某种方法挑选出 t o p top top u u u个queries,组成 Q − Q^- Q− 。
将u定义为 u = c ∗ L n Q u=c*LnQ u=c∗LnQ ,c是超参数,所以query的数量是 O ( L n Q ) O(LnQ) O(LnQ)级的,而key的数量是 L n k Lnk Lnk个,所以共有 O ( L n Q ∗ L k ) O(LnQ*L_k) O(LnQ∗Lk)个点积需要计算。自然而然地,时间复杂度就降为了 O ( L n Q ∗ L k ) O(LnQ*L_k) O(LnQ∗Lk)。
值得注意的是:这种方法,相比之前学者们的启发式方法,还有一个好处,那就是在多头视角下,这种注意力为每个头生成不同的稀疏的“查询-键对”(query-key pairs),从而避免了严重的信息丢失作为回报。
然而,遍历测量 M ( q i ; K ) M(qi;K) M(qi;K) 的所有query查询需要计算每个点积对,才能选出前 t o p top top u u u个query即二次方的计算复杂度 O ( L Q ∗ L K ) O(L_Q*L_K) O(LQ∗LK),此外 LSE 操作具有潜在的数值稳定性问题。
![]()
所以作者用一种近似改进了公式如下(如上图中用上界来代替那个LSE):
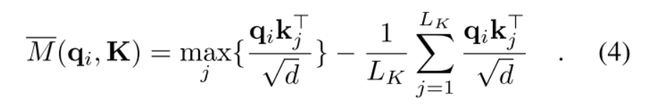
(该引理的证明在原论文附录 D.1和2,这里面的推理确实很复杂! )
在长尾分布下,我们只需要随机抽取 U = L Q ∗ L n K U=L_Q*Ln_K U=LQ∗LnK 个“点积对”(dot-product pairs)来计算 M ( q i , k ) M(q_i,k) M(qi,k),即用零填充其他对。
然后,我们从中选择稀疏的 Top-u 作为 Q − Q^- Q−。

具体计算步骤详情如下:
Q,K,V为输入的embedding分别乘上一个权重矩阵得到的query、key、value。ProbSparse Self-Attention首先对K进行采样,得到K_sample,对每个 q i ∈ Q q_i\in Q qi∈Q 关于K_sample求M值:

找到M值最大的u个 q i q_i qi ,对这Top-u个 q i q_i qi 关于K求score值:

其中 Q − Q^- Q−是Top-u的 q i q_i qi 组成的矩阵,这样就得到了 S 0 S_0 S0,对于没有被选中的那些 q i q_i qi的score值取 m e a n ( V ) mean(V) mean(V),来保证输入和输出序列长度都是 L L L。
注意:ProbSparse Attention 在为每个query随机采样key时,每个head的采样结果是相同的,也就是采样的key是相同的。但是由于每一层self-attention都会先对Q、K、V做线性转换,这使得序列中同一个位置上不同head对应的query、key向量不同,所以每个head的同一个query的sparsity measurement都不相同,这就使得每个head中得到的前u个measurement 最高的query也是不同的。这也等价于每个head都采取了不同的优化策略。
之前一篇粗读,对这里理解是有点误差的。
1.2.3 encoder 处理长序列输入
即使在内存使用受限的情况下允许更长的序列输入:
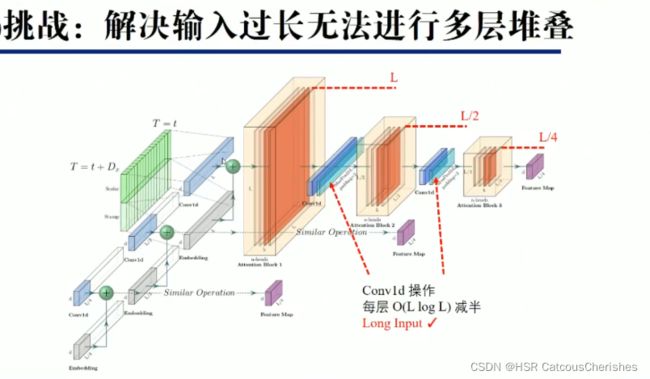
提出了自注意力蒸馏的操作,具体是在相邻的Attention Block之间加入卷积池化操作,来对特征进行降采样。
Informer中的Distilling操作,本质上就是一个1维卷积+ELU激活函数+最大池化。公式如下:
![]()
Distilling操作这一块的代码实现:
import torch
import torch.nn as nn
import torch.nn.functional as F
class ConvLayer(nn.Module):
def __init__(self, c_in):
super(ConvLayer, self).__init__()
self.downConv = nn.Conv1d(in_channels=c_in,
out_channels=c_in,
kernel_size=3,
padding=2,
padding_mode='circular')
self.norm = nn.BatchNorm1d(c_in)
self.activation = nn.ELU()
self.maxPool = nn.MaxPool1d(kernel_size=3, stride=2, padding=1)
def forward(self, x):
x = self.downConv(x.permute(0, 2, 1))
x = self.norm(x)
x = self.activation(x)
x = self.maxPool(x)
x = x.transpose(1,2)
return x
具体的encoder模块代码,需要去仔细查看源码!
1.2.4 Decoder输出提速
![]()
上面介绍的这样生成式的输出,避免了之前的依赖前一个输出的一种动态解码的限制,大大的加快了长序列的输出!
Decoder部分结构可以参考Transformer中的Decoder结构,包括两层attention层和一个两层线性映射的Feed Forward部分。
需要注意的是,第一个attention层中的query、key、value都是根据Decoder输入的embedding乘上权重矩阵得到的,而第二个attention层中的query是根据前面attention层的输出乘上权重矩阵得到的,key和value是根据Encoder的输出乘上权重矩阵得到的。
import torch
import torch.nn as nn
import torch.nn.functional as F
class DecoderLayer(nn.Module):
def __init__(self, self_attention, cross_attention, d_model, d_ff=None,
dropout=0.1, activation="relu"):
super(DecoderLayer, self).__init__()
d_ff = d_ff or 4*d_model
self.self_attention = self_attention
self.cross_attention = cross_attention
self.conv1 = nn.Conv1d(in_channels=d_model, out_channels=d_ff, kernel_size=1)
self.conv2 = nn.Conv1d(in_channels=d_ff, out_channels=d_model, kernel_size=1)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.norm3 = nn.LayerNorm(d_model)
self.dropout = nn.Dropout(dropout)
self.activation = F.relu if activation == "relu" else F.gelu
def forward(self, x, cross, x_mask=None, cross_mask=None):
x = x + self.dropout(self.self_attention(
x, x, x,
attn_mask=x_mask
)[0])
x = self.norm1(x)
x = x + self.dropout(self.cross_attention(
x, cross, cross,
attn_mask=cross_mask
)[0])
y = x = self.norm2(x)
y = self.dropout(self.activation(self.conv1(y.transpose(-1,1))))
y = self.dropout(self.conv2(y).transpose(-1,1))
return self.norm3(x+y)
class Decoder(nn.Module):
def __init__(self, layers, norm_layer=None):
super(Decoder, self).__init__()
self.layers = nn.ModuleList(layers)
self.norm = norm_layer
def forward(self, x, cross, x_mask=None, cross_mask=None):
for layer in self.layers:
x = layer(x, cross, x_mask=x_mask, cross_mask=cross_mask)
if self.norm is not None:
x = self.norm(x)
return x
每个DecoderLayer的内部,包括:
一个self-attention;
一个cross-attention,负责target sequence和source sequence的交互用的;
两个conv1,是512 -> 2048 -> 512用的,类似FFN;
三个layer norm
一个dropout
上面使用的比较重要的,分别是self_attention(用的是ProbAttention)和cross_attention(用的是FullAttention)。
1.3 informer模型的总体架构

小结: 对于informer的理解,informer:告密者,线人,就如同他的名字一样去理解,从过去到现在告诉我们事物的发展趋势,从而解决预测长序列的三大难题!
比如ProbSparse self-attention 做的事情其实也是在告诉我们历史数据中的重要信息,以确定预测时需要考虑的重要因素!
1.4 实验部分与结果分析
1.4.1 实验数据集与比较模型,以及评估指标

I n f o r m e r + Informer^+ Informer+是将所有的ProbSparse Attention换成标准的self-attention,我们可以看到,很多情况下, I n f o r m e r Informer Informer 效果竟然比 I n f o r m e r + Informer^+ Informer+还要好,作者认为这说明ProbSparse self-attention去掉了一些冗余的信息。
我们可以看到, I n f o r m e r Informer Informer 共取得了28 项SOTA;多变量也取得了类似的结论。
1.4.2 消融实验
消融实验一:
下图是对 self-attention的消融实验,探讨的是针对的attention(右边方框中红色部分)部分的区别。 I n f o r m e r + Informer^+ Informer+是将所有的ProbSparse Attention换成标准的self-attention。
我们可以看到,当输入序列长度为1440时,中间两个模型已经无法处理了,而Informer和Reformer依然坚挺,但是Informer效果要好很多;以及输入越长,效果会越好。
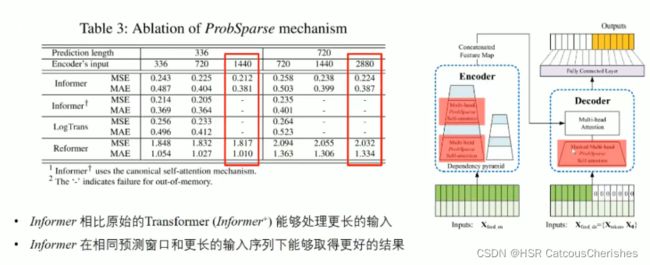
消融实验二:
下图是对自注意力蒸馏操作的消融实验。 I n f o r m e r + + Informer^{++} Informer++模型是使用原始self-attention并移除卷积蒸馏操作,在输入长度为720时取得了好的效果,但是无法处理更长的输入。
I n f o r m e r + Informer^+ Informer+ 对于更长的预测,更长的输入带来的性能提升更加明显。

消融实验三:
下图是对生成式Decoder的消融实验结果。
I n f o r m e r + + Informer^{++} Informer++模型是使用原始self-attention并移除卷积蒸馏操作,也就是只保留生成式Decoder部分;下面那个模型是从 I n f o r m e r + + Informer^{++} Informer++模型中再移除生成式Decode,用原始的动态解码过程代替。
我们可以看到,生成式Decoder比传统的动态编码效果要好,这可能是因为动态编码存在这错误传递的问题。

1.5 Informer模型的预测效果对比
二. 力源项目数据据库相关问题
2.1 产品二维码数据库表更新同步到云数据库
由于之前没有开放安全端口,无法获取远程访问权限,无法实现存储过程与数据库连接同步的设置,所以目前的解决方案是手动更新数据库。
下面是数据库保持同步的详细步骤:
-
分别远程登入两台机器,打开navicat,找到这个poc_packcode_client数据库中的packcodeinfo表,进行转储为sql 文件,并都发送至云服务器上(分别是A和B)
-
打开云服务器上的数据库,找到packcodeinfo 表将其重命名为-> packcodeinfo1
-
分别运行转储的那两个sql文件,运行好后,分别提前 改名为A+日期
-
再将其命名恢复 packcodeinfo1 -> packcodeinfo
分别:
-
设计两个新转储的表,右键 设计表 ,取消主键, 添加 chuku,jxs,cky 三个字段 varchar 255
-
按照日期查询,日期是上次对应表的最后一条数据的CreatedDate
-
合并更新,日期是上次对应表的最后一条数据的下一条数据CreatedDate
-
即可完成数据库更新同步
-
这一方案耗时严重却繁琐!
2.2 改进方案
下面申请开放云服务器的安全端口(例如:5555) ,为安全起见,不对外公开,随机选取一个不被占用的端口即可。
开放云服务器的安全端口可参考:开放端口设置详情,简单介绍开放云端口;
更改好了连接mysql 的安全端口之后,便是需要修改mysql 的默认端口号3306,将刚刚设置的安全端口,修改与其对应即可。
如何修改mysql的默认端口号:可参考怎么修改mysql的默认端口号
修改好了mysql 的端口,那随之需要改变的就是修改云服务器上的 数据库连接代码,具体就不详细记录了,大致就是将所有后端和数据库交互会用到数据库的地方全部添加修改后的端口号,APP端不用修改。
2.3下一步具体实现自动同步
难点: 云服务器与无固定IP的多个本地实现按条件执行同步!
改进的下一步就是配置第三方远程连接同步数据库软件,去实现数据库表的同步更新,但具体过程还得去和师兄商榷,这里还需要进一步增加同步得字段,按什么去实现云同步。目前先在本地测试是否可以做到按日期同步更新,并添加所需要得字段,再合并到数据库表中,最重要的是不遗漏数据和不延迟。
2.4 另:关于手机定位显示在web页面功能得实现
三. 深度学习基础知识
四.总结
一是已经有大量的学习者复现了informer,也可以将该模型应用在生物,环境等科学领域内,看能否实现较为不错的结果!论文全部代码理解起来还是有很大难度的,对于现阶段来说,这也将作为与Autoformer模型的代码来对比学习与复现任务。
二是继续学习与优化数据库的同步更新,以及更进该项目。