Spark.SQL时间序列缺失值填充与异常值处理
PySpark时间序列缺失值填充与异常值处理
- 1 缺失值填充
-
- 1.就近填充
- 2.同周期填充
- 2 异常值处理
-
- 1.特殊事件标注
- 2.业务常识约束
- 3.分位数(quantile)盖帽
- 4.n-sigma盖帽
- 5.平滑方法
- 3. 总结
本文为销量预测第3篇:缺失值填充与异常值处理
第1篇:PySpark与DataFrame简介
第2篇:PySpark时间序列数据统计描述,分布特性与内部特性
第4篇:时间序列特征工程
第5篇:特征选择
第6篇:简单预测模型
第7篇:线性回归与广义线性模型
第8篇:机器学习调参方法
第9篇:销量预测建模中常用的损失函数与模型评估指标
在PySpark中相应的数据缺失模块为pyspark.ml.feature.Imputer,对缺失值nan/Null提供Mean和Median的填充方式。由于时序数据本身的特殊性,简单使用均值或者中位数填充不是最优选择,甚至破环数据原始规律。同时,真实的数据中或许还存在异常值,而缺失值和异常值的处理是在特征工程之前需要解决的,否则在原始数据之上加工的特征也将变得"不干净",该问题尤其存在于时序这种严重依赖过去历史数据进行机器学习建模的场景中,以下将结合代码详细讲解缺失值填充与异常值修复。
1 缺失值填充
一个完整的序列,缺失值为0,由于某些因素,缺失了若干时间点的数据,就需要补全缺失值。如果删除或者忽略缺失的数据将存在以下问题:
1):针对单个序列使用时间序列预测时,删除意味着无法直接通过该序列预测未来的时间点。
2):直接删除或是无视数据项使得时间序列数据相关数据项的时间关联属性被破坏,造成删除缺失项后的数据集与真实数据集在数据时间联系上存在差别。
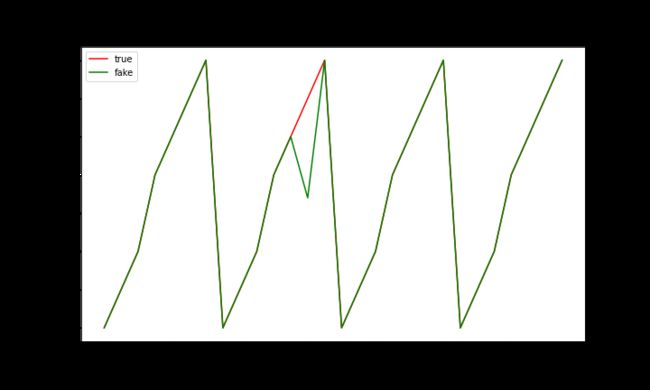
同时,时序数据对数据出现的位置敏感,常规的均值/众数填充不合适,这将影响序列的周期性,趋势等规律,扭曲其分布,如果使用回归法插补的前提是缺失项和观测值之间存在线性关系,且填补的缺失值估计也会趋向于均值。在一个具有以7天为周期的完整序列中,如果把其中的一个值替换为均值,将打乱序列的周期规律性。
在一个具备持续增长趋势的序列中,如果将其中一天的序列使用均值替换将得到一个具有局部下降的序列,该序列的结构也将得到破环。如下图
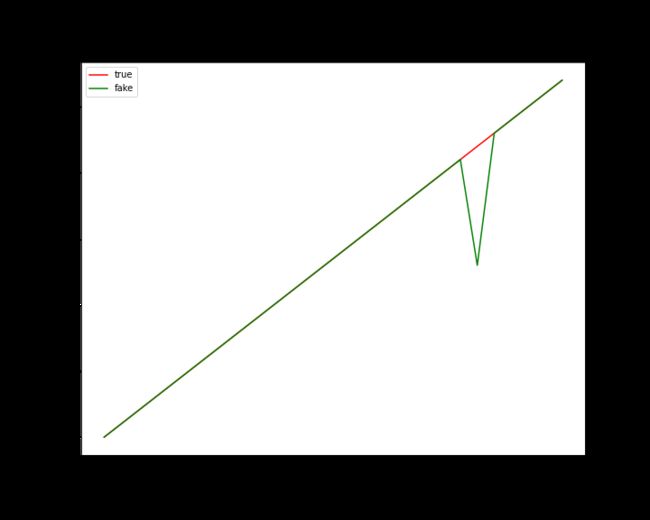
总的来说,合适的缺失值处理算法能够最大化的减少偏差,使得插补后的数据集与真实数据集更为贴近,降低因缺失值对数据的分析和应用的影响。
由于时间序列数据对数据出现的位置敏感,下文将通过以下两种简单的策略进行填充:
1.就近填充
为防止后续特征加工过程中的数据穿越,建议使用向前(forward fill)填充,不使用后向填充(back fill)的方式;使用缺失值前的一个,或几个的均值进行填充。
2.同周期填充
越近的数据越重要,上一个周期和上上周期的数据填充越合理。
所以,针对有零售销售以7天为一个周期性的数据,前向依次填充:前一天的销售,前7天的销售数据,前14天的销售数据,如果依然没有填充上,则填充为0。
with lag_bef as (select
shop_id,
sku_id,
sale_date,
sale_qty,
case when sale_qty is null then 1 else 0 end as miss_label,
lag(sale_qty,1) over(partition by shop_id,sku_id order by sale_date) as lag1_qty,
lag(sale_qty,7) over(partition by shop_id,sku_id order by sale_date) as lag7_qty,
lag(sale_qty,14) over(partition by shop_id,sku_id order by sale_date) as lag14_qty
from fill_null_set),
lag1_fill as (select shop_id,sku_id,sale_date,miss_label,nvl(sale_qty,lag1_qty) as sale_qty,lag7_qty,lag14_qty from lag_bef),
lag7_fill as (select shop_id,sku_id,sale_date,miss_label,nvl(sale_qty,lag7_qty) as sale_qty,lag14_qty from lag1_fill),
lag14_fill as (select shop_id,sku_id,sale_date,miss_label,nvl(sale_qty,lag14_qty) as sale_qty from lag7_fill)
select shop_id,sku_id,sale_date,miss_label,nvl(sale_qty,0) as sale_qty from lag14_fill
除了向前填充的几种方式外,还有KNN以及插值填充法,不过由于确定超参数k值的不便,以及插值方式要求序列数据为线性关系计算复杂度比较高,读者也可以自行尝试。
需要说明的是,填补的数据只是尽量还原数据原始的面貌,并不能完全代替真实情况,所以如果存在缺失值,即使序列数据已经补全,也有一定的失真,且更严重的是,如果缺失的值比较多,需要填充更多的值,相比较完整的序列,自然更加不好预测。针对同一个序列中缺失值(销售中断)很多的情况下,再去补全序列值,往往并不可行,此时需要区分缺失值是否是由于该时间点没有发生值导致的,比如在零售领域某些sku在很多天没有销售记录,也就是销售记录连续多天为0,此时有专门针对这种间断需求(Intermittent demand)的预测方法如Croston’s method。
2 异常值处理
在处理完了缺失值以后,下面讲解序列中的异常值处理办法。不处理异常值,会导致模型错误的估计;简单地替换或者删除异常值(离群值)而不考虑它们产生的原因也是一种危险的做法,因为异常值可能提供与产生数据过程有关的有用信息,在预测时应该考虑这些信息。
针对序列中存在的异常值,通常有以下几种方式:
1.特殊事件标注
如数据中存在的异常是已知或者结合业务背景能探明的某些如促销因素引起的异常,那么,针对该异常值,首先对已知因素引起异常的相关数据标注,生成一个新的特征列。也就是生成一个虚拟变量,来处理数据中的异常值 ,与简单删除离群点不同的是,虚拟变量剔除了离群点对模型的影响。当该观测值是离群点时,虚拟变量取值为1,在其他观测值处,虚拟变量取值均为0,用来表示特殊事件是否发生。如果已经把异常值产生的原因已经找到,且已经生成了多个特征来表示,在后面机器学习建模任务中纳入这个特征,在拟合过程中,模型通给予该特征响应的权重系数,拟合该特殊事件。
select
shop_number,
sku_number,
sale_date,
sale_qty,
case when sale_date in ('2020-11-20','2020-12-03') then 1 else 0 end as year_end_promotion
from temp.forecast_feature
2.业务常识约束
实践中还需结合实际业务或者数据分布情况,把销售值限定在某一个合理的区间,削去大于极大值的点和小于极小值的点。该方法需要探索数据或者结合业务情况,比如门店的单品当天销量不可能超过1000,也不会低于0。
select
shop_number,
sku_number,
case when sale_qty<0 then 0 when sale_qty>1000 then 1000 else sale_qty end as sale_qty
from temp.forecast_feature
以上两种方式的优先级最高,需结合业务知识,在此基础上才通过下面将要介绍的统计方法或者算法修复异常值问题。
3.分位数(quantile)盖帽
针对超过如90%的分位数限定为90%,同理,对低于10%分位数的销售数据等于10%。
实例代码如下:
with percent_smooth as (
select
shop_number,
sku_number,
percentile(int(sale_qty), 0.1) as low_sale,
percentile(int(sale_qty), 0.9) as high_sale
from temp.forecast_feature
group by
shop_number,
sku_number)
select
a.shop_number,
a.sku_number,
a.sale_date,
case when a.sale_qty > b.high_sale then high_sale
when a.sale_qty < b.low_sale then low_sale
else a.sale_qty
end as sale_qty
from temp.forecast_feature a
left join percent_smooth b
on a.shop_number=b.shop_number and a.sku_number=b.sku_number
4.n-sigma盖帽
分位数盖帽是按照数据的分位数进行限定,而n-sigma则是按照数据均值和标准差进行约束的方式。
在 正 态 分 布 中 σ 代 表 标 准 差 , μ 代 表 均 值 数 值 分 布 在 ( μ — σ , μ + σ ) 中 的 概 率 为 0.6526 数 值 分 布 在 ( μ — 2 σ , μ + 2 σ ) 中 的 概 率 为 0.9544 数 值 分 布 在 ( μ — 3 σ , μ + 3 σ ) 中 的 概 率 为 0.9974 在正态分布中σ代表标准差,μ代表均值\\ 数值分布在(μ—σ,μ+σ)中的概率为0.6526\\ 数值分布在(μ—2σ,μ+2σ)中的概率为0.9544\\ 数值分布在(μ—3σ,μ+3σ)中的概率为0.9974\\ 在正态分布中σ代表标准差,μ代表均值数值分布在(μ—σ,μ+σ)中的概率为0.6526数值分布在(μ—2σ,μ+2σ)中的概率为0.9544数值分布在(μ—3σ,μ+3σ)中的概率为0.9974
n-sigma盖帽语法同上文分位数盖帽,Spark.SQL如下:
with n_sigma_smooth as (
select shop_number, sku_number,
avg(sale_qty) + 2 * stddev(sale_qty) as up_sale,
avg(sale_qty) -2 * stddev(sale_qty) as low_sale
from temp.forecast_feature
group by shop_number, sku_number)
select
a.shop_number,
a.sku_number,
a.sale_date,
case when a.sale_qty > b.up_sale then b.up_sale
when a.sale_qty<b.low_sale then b.low_sale
else a.sale_qty
end as sale_qty
from temp.forecast_feature a
left join n_sigma_smooth b
on a.shop_number=b.shop_number and a.sku_number=b.sku_number
需要注意的是,n-sigma假定数据是正态或者接近正态,相比较而言分位数平滑盖帽法更加稳健。
5.平滑方法
时序中常见的平滑降噪方法,如指数平滑(Exponential Smoothing),对序列中存在的局部极值进行平滑,或者使用多项式(Polynomial Smoothing),甚至使用局部加权线性回归(Locally Weighted Regression, LWR)进行拟合,关于平滑方法的代码示例请参照个人所写另一篇文章。
3. 总结
以上几种方式,特殊事件标注应该是最早开始处理,后续的处理应该剔除标注过属于异常时间引起的异常数据,然后再进行计算分位数或均值,否则计算得到的统计量会因这些异常带偏,由于在需求预测领域,需求的发生往往不呈正态分布,而是如指数分布中的泊松分布,或者其他的有偏分布,此时使用基于分位数的方式,往往比基于均值的n-sigma 方式更加可信。最后介绍的指数平滑方法,对数据分布也没有过多分布上的假设,只假定最近的数据点对当前序列值影响最大。