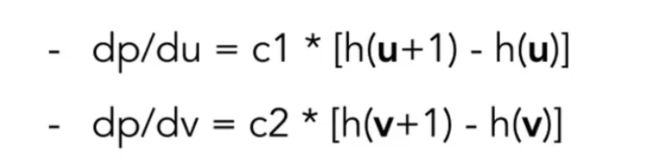games101,作业3
1.配置环境
- 使用c++17及以上版本,因为optional这个类是c++17才推出来的新类。
- 改变main.cpp中
std::string obj_path = "./models/spot/";
bool loadout = Loader.LoadFile("./models/spot/spot_triangulated_good.obj");
路径为自己的相对路径。
- 将前面代码中的
get_projection_matrix函数拷贝过来。
2.任务1
TODO: From your HW3, get the triangle rasterization code.
将前一个作业的代码复制粘贴过来。
伪代码:
确定boundingbox的l,r,t,b;
for(int x=l;x<r;x++){
for(int y=b;y<t;y++){
if((x,y)在三角形内){
循环;
}
}
}
注意
- 不使用反走样技术
- 在作业3的框架中,有函数
static bool insideTriangle(int x, int y, const Vector4f* _v),替代了自己在作业2中写的函数,这里注意要改写。insideTriangle(x+0.5f, y+0.5f, t.v)。
TODO: Inside your rasterization loop:
- v[i].w() is the vertex view space depth value z.。
- v[i].w()是顶点视图空间深度值z。
- Z is interpolated view space depth for the current pixel。
- Z为当前像素插值视图空间深度 。
- zp is depth between zNear and zFar, used for z-buffer。
- zp在zNear和zFar之间的深度,用于z缓冲区 。
计算alpha,beta,gamma
相关细节参照我的另一篇blog
c++17以上版本支持
auto [alpha, beta, gamma] = computeBarycentric2D(x+0.5f, y+0.5f, t.v);
c++11以上版本
auto p = computeBarycentric2D(x, y, t.v);
float alpha = std::get<0>(p);
float beta = std::get<1>(p);
float gamma = std::get<2>(p);
计算深度zp
使用教程自带代码计算。
float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
zp *= Z;
TODO: Interpolate the attributes:
线性插值属性
线性插值: 插 值 = α A + β B + γ C 插值 =\alpha A+\beta B+ \gamma C 插值=αA+βB+γC
- auto interpolated_color 颜色
- auto interpolated_normal 法线
- auto interpolated_texcoords 纹理坐标
- auto interpolated_shadingcoords 屏幕坐标
线性插值函数
在rasterize类中有如下函数,是框架自带的函数,我们在线性插值时看直接使用。
注意:参数的最后有个float weight,会对线性插值出来的值除以这个数,这里我们传入1.0f
static Eigen::Vector3f interpolate(float alpha, float beta, float gamma, const Eigen::Vector3f& vert1,
const Eigen::Vector3f& vert2, const Eigen::Vector3f& vert3, float weight)
{
return (alpha * vert1 + beta * vert2 + gamma * vert3) / weight;
}
static Eigen::Vector2f interpolate(float alpha, float beta, float gamma, const Eigen::Vector2f& vert1,
const Eigen::Vector2f& vert2, const Eigen::Vector2f& vert3, float weight)
{
auto u = (alpha * vert1[0] + beta * vert2[0] + gamma * vert3[0]);
auto v = (alpha * vert1[1] + beta * vert2[1] + gamma * vert3[1]);
u /= weight;
v /= weight;
return Eigen::Vector2f(u, v);
}
插值代码
//颜色
auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1);
//法线
auto interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1).normalized();
//纹理坐标
auto interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1);
//屏幕坐标
auto interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1);
注意,我们在计算法线时使用了.normalized(),将法线标准化,这里也可以不添加,只要在下面传入法线参数时标准化即可。
将计算好的参数传入片元着色器
fragment_shader_payload payload( interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);payload.view_pos = interpolated_shadingcoords;
Instead of passing the triangle’s color directly to the frame buffer, pass the color to the shaders first to get the final color;
不使用直接传入三角形颜色到屏幕缓存,而是使用将颜色传入shader,再通过shader得到最终的颜色。
auto pixel_color = fragment_shader(payload);
设置屏幕像素颜色
在作业二中,我们使用了set_pixel(Eigen::Vector3f(x, y, z_interpolated), t.getColor());,那我们把t.getColor()变为pixel_color是不是就行了???
程序报错

我一开始以为时Eigen库的版本出了问题,或是Eigen库不支持c++17以上版本!!!!
后来才知道,并不是!!!!!
- 第一个问题,你将不同大小的矩阵混合。
- 第二个问题,你将不同的数字类型混合,你需要使用强制转换来明确数据类型。
找到问题在最后一行set_pixel(Eigen::Vector3f(x, y, zp), pixel_color);这个函数花了我不知多少时间。。。。。
毕竟这里没有告诉你问题在整个框架的哪一处。
我们看一下出问题的这个函数:
void rst::rasterizer::set_pixel(const Vector2i &point, const Eigen::Vector3f &color)
{
//old index: auto ind = point.y() + point.x() * width;
int ind = (height-point.y())*width + point.x();
frame_buf[ind] = color;
}
这里传入两个参数,第一个参数传入Vector2i,这与作业2中的set_pixel不同
作业2中有:
void rst::rasterizer::set_pixel(const Eigen::Vector3f& point, const Eigen::Vector3f& color)
{
//old index: auto ind = point.y() + point.x() * width;
auto ind = get_index(point.x(), point.y());
frame_buf[ind] = color;
}
这里第一个参数是Eigen::Vector3f。
- Vector3 → \rightarrow →Vector2 是第一个问题
- Vectorf → \rightarrow → Vectori 是第二个问题
因此这里需要改变set_pixel函数的使用:
set_pixel(Eigen::Vector2i(x, y), pixel_color);
程序运行
在VS2019 → \rightarrow →项目属性配置 → \rightarrow →调试 → \rightarrow →命令参数 中输入 output.png normal
注意配置环境是Dubug还是Release。
然后运行。

在项目文件下出现output.png文件,打开后如下。

至此,任务1完成。
任务3 blinn-phong模型
任务3涉及的blinn-phong模型实现 与 OpenGL中fragmentShader(片元着色器)中对片元的操作方式相同,这里就不赘述。
补充:ka.cwiseProduct(amb_light_intensity);中cwiseProduct表示对Matrix直接进行点对点乘法。
例如:
[ 1 3 5 9 ] ∗ [ 1 2 3 4 ] = [ 1 6 15 36 ] \begin{bmatrix}1 & 3 \\ 5 & 9\\ \end{bmatrix}*\begin{bmatrix}1 & 2 \\ 3 & 4\\ \end{bmatrix}=\begin{bmatrix}1 & 6 \\ 15 & 36\\ \end{bmatrix} [1539]∗[1324]=[115636]
任务4 纹理
texture的实现只需要将纹理坐标对应的颜色传给return_color.
fragment_shader_payload payload存储了
Eigen::Vector3f view_pos;//摄像机位置
Eigen::Vector3f color;//片元颜色
Eigen::Vector3f normal;//法线
Eigen::Vector2f tex_coords;//纹理坐标
Texture* texture;//纹理
其中Texture* texture有
参数
int width, height;
保存图片的长宽。
函数
Eigen::Vector3f getColor(float u, float v)
{
auto u_img = u * width;
auto v_img = (1 - v) * height;
auto color = image_data.at<cv::Vec3b>(v_img, u_img);
return Eigen::Vector3f(color[0], color[1], color[2]);
}
返回图片u,v点的颜色。
补充:这里的纹理坐标会出现负值,所以对它进行了限定。
Eigen::Vector3f getColor(float u, float v)
{
// 坐标限定
if (u < 0) u = 0;
if (u > 1) u = 1;
if (v < 0) v = 0;
if (v > 1) v = 1;
auto u_img = u * width;
auto v_img = (1 - v) * height;
auto color = image_data.at<cv::Vec3b>(v_img, u_img);
return Eigen::Vector3f(color[0], color[1], color[2]);
}
原文链接:https://blog.csdn.net/qq_36242312/article/details/105888669
所以使用如下代码实现将纹理坐标对应的颜色传给return_color.
return_color = payload.texture->getColor(payload.tex_coords.x(), payload.tex_coords.y());
再使用phong光照模型渲染。
但还是会有如下报错,问题出在哪里不得知。
![]()
但这不影响最终图片的生成。

任务5 凹凸贴图
修改函数 bump_fragment_shader() in main.cpp: 在实现 Blinn-Phong 的
基础上,仔细阅读该函数中的注释,实现 Bump mapping.

如果想详细了解法线贴图的细节,可以浏览:
- Tutorial 13 : Normal Mapping
这个网站是英文版的 - 法线贴图
这个是OpenGL中文版教程
下面我简要的介绍一些法线贴图
TNB矩阵
可以把切线空间的z方向和表面的法线方向对齐。
这种矩阵叫做TBN矩阵这三个字母分别代表tangent(切线)、bitangent(副切线)和normal向量。这是建构这个矩阵所需的向量。
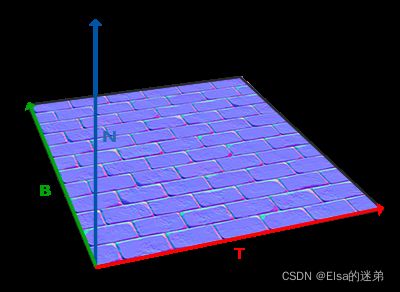
从图中可以看到法线贴图的切线和副切线与纹理坐标的两个方向对齐。我们就是用到这个特性计算每个表面的切线和副切线的。
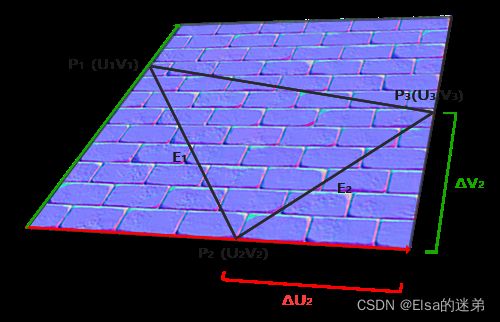
[ T x T y T z B x B y B z ] = 1 Δ U 1 Δ V 2 − Δ U 2 Δ V [ Δ V 2 − Δ V 1 − Δ U 2 Δ U 1 ] [ E 1 x E 1 y E 1 z E 2 x E 2 y E 2 z ] \begin{bmatrix}Tx & Ty & Tz \\ Bx & By & Bz\\ \end{bmatrix} = {1\over ΔU1ΔV2−ΔU2ΔV} \begin{bmatrix} ΔV2 & -ΔV1 \\ -ΔU2 & ΔU1 \end{bmatrix} \begin{bmatrix}E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \\ \end{bmatrix} [TxBxTyByTzBz]=ΔU1ΔV2−ΔU2ΔV1[ΔV2−ΔU2−ΔV1ΔU1][E1xE2xE1yE2yE1zE2z]
可求出T,B向量
计算出切线和副切线你就已经部分地达到目的了
代码实现
代码任务
// TODO: Implement bump mapping here
1.计算TBN,可使凹凸贴图中的(0,0,1)变化为世界坐标中的贴图法向量。
// Let n = normal = (x, y, z)
// Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
这里计算T的方式与教程中有很大差异,
// Vector b = n cross product t
// Matrix TBN = [t b n]
代码实现:
float x = normal.x();
float y = normal.y();
float z = normal.z();
Eigen::Vector3f t{ x * y / std::sqrt(x * x + z * z), std::sqrt(x * x + z * z), z*y / std::sqrt(x * x + z * z) };
Eigen::Vector3f b = normal.cross(t);
Eigen::Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
2.法线变化
kh,kn为常数
dU为纹理坐标在u方向上的(离散)导数
dV同理
// dU = kh * kn * (h(u+1/w,v)-h(u,v))
// dV = kh * kn * (h(u,v+1/h)-h(u,v))
Vector ln为纹理坐标点的法向量
// Vector ln = (-dU, -dV, 1)
世界坐标系中该点法向量为TBN*ln。
// Normal n = normalize(TBN * ln)
代码实现:
float u = payload.tex_coords.x();
float v = payload.tex_coords.y();
float w = payload.texture->width;
float h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColor(u + 1.0f / w , v).norm() - payload.texture->getColor(u, v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1.0f / h).norm() - payload.texture->getColor(u, v).norm());
Eigen::Vector3f ln{ -dU,-dV,1.0f };
normal = TBN * ln;
// 归一化
Eigen::Vector3f result_color = normal.normalized();
return result_color * 255.f;
GAMES101-现代计算机图形学学习笔记(作业03)
任务6 位移贴图
displacement_fragment_shader是在上面求出新的法向量的基础上应用了布林冯模型。
按照games101教程所说,位移贴图实际改变了三角形的顶点,并不是在凹凸贴图上使用blinn-phong模型。

directX使用了动态曲面细分,使得位移贴图能最大程度的优化运行。
这与OpenGL是有区别的。
这里就不说位移贴图的实现了。