FCN源码解读之surgery.py
转载自 https://blog.csdn.net/qq_21368481/article/details/80289350
surgery.py是FCN中用于转换模型权重的python文件,在解读源码前,我们先来看一下VGG16网络的构架和FCN32s网络的构架两者之间的区别(此处参看VGG_ILSVRC_16_deploy.prototxt和FCN32s的deploy.prototxt,deploy.prototxt文件比train.prototxt文件少了输入层的数据路径和loss层的反向传播,其余网络结构两者是一样的),如下:| VGG16 | FCN32s |
|
|
从上表两个网络的配置文件中可以看出,FCN32s的网络结构和VGG16的不部分是相同的,特别是前面的卷积层(均用RuLe激活函数)、池化层(均用最大池化),这些层的卷积核大小、步长和填充数(除了第一个卷积层的填充数不一样)都是一样的,不同的地方在于后面的fc6和fc7层,VGG16的这两层是全连接层,FCN32s的是卷积层,还有一点不同是FCN32s去掉了VGG16的fc8层。
但实际上网络卷积层的参数与卷积核的步长和填充数是没有关系的,只与卷积核的大小,以及该层的输入通道数和输出通道数(输出特征图的数目)有关,且最大池化层无需训练参数。所以可以采用直接将VGG16训练好的模型参数初始化FCN32s网络各层的权重和偏置,但由于VGG16的fc6和fc7是全连接层,其参数需要经过一定的排列才能赋值给FCN32s的fc6和fc7层(FCN32s这两层是卷积层)。由此需要surgery.py来实现VGG16参数赋值给FCN32s网络。
surgery.py的源代码如下:
-
from __future__
import division
-
import caffe
-
import numpy
as np
-
-
def transplant(new_net, net, suffix=''):
-
"""
-
Transfer weights by copying matching parameters, coercing parameters of
-
incompatible shape, and dropping unmatched parameters.
-
-
The coercion is useful to convert fully connected layers to their
-
equivalent convolutional layers, since the weights are the same and only
-
the shapes are different. In particular, equivalent fully connected and
-
convolution layers have shapes O x I and O x I x H x W respectively for O
-
outputs channels, I input channels, H kernel height, and W kernel width.
-
-
Both `net` to `new_net` arguments must be instantiated `caffe.Net`s.
-
"""
-
for p
in net.params:
-
p_new = p + suffix
-
if p_new
not
in new_net.params:
-
print
'dropping', p
-
continue
-
for i
in range(len(net.params[p])):
-
if i > (len(new_net.params[p_new]) -
1):
-
print
'dropping', p, i
-
break
-
if net.params[p][i].data.shape != new_net.params[p_new][i].data.shape:
-
print
'coercing', p, i,
'from', net.params[p][i].data.shape,
'to', new_net.params[p_new][i].data.shape
-
else:
-
print
'copying', p,
' -> ', p_new, i
-
new_net.params[p_new][i].data.flat = net.params[p][i].data.flat
-
-
def upsample_filt(size):
-
"""
-
Make a 2D bilinear kernel suitable for upsampling of the given (h, w) size.
-
"""
-
factor = (size +
1) //
2
-
if size %
2 ==
1:
-
center = factor -
1
-
else:
-
center = factor -
0.5
-
og = np.ogrid[:size, :size]
-
return (
1 -
abs(og[
0] - center) / factor) * \
-
(
1 - abs(og[
1] - center) / factor)
-
-
def interp(net, layers):
-
"""
-
Set weights of each layer in layers to bilinear kernels for interpolation.
-
"""
-
for l
in layers:
-
m, k, h, w = net.params[l][
0].data.shape
-
if m != k
and k !=
1:
-
print
'input + output channels need to be the same or |output| == 1'
-
raise
-
if h != w:
-
print
'filters need to be square'
-
raise
-
filt = upsample_filt(h)
-
net.params[l][
0].data[range(m), range(k), :, :] = filt
-
-
def expand_score(new_net, new_layer, net, layer):
-
"""
-
Transplant an old score layer's parameters, with k < k' classes, into a new
-
score layer with k classes s.t. the first k' are the old classes.
-
"""
-
old_cl = net.params[layer][
0].num
-
new_net.params[new_layer][
0].data[:old_cl][...] = net.params[layer][
0].data
-
new_net.params[new_layer][
1].data[
0,
0,
0,:old_cl][...] = net.params[layer][
1].data
源码解读如下:
(1)transplant()函数
-
def transplant(new_net, net, suffix=''):
-
"""
-
通过复制匹配的参数来传递权重,强制网络形状不兼容的参数以及丢弃不匹配的参数。
-
强制将全连接层转换为等效的卷积层是有用的,因为权重是相同的,只是网络的形状不同。特别地,等效的全连接层和卷积层分别具有形状O x I和O x I x H x W,其中O为输出通道数,I输入通道数,H为卷积核高度和W为卷积核宽度。
-
`net`到`new_net`参数都必须实例化`caffe.Net`s。
-
-
Transfer weights by copying matching parameters, coercing parameters of
-
incompatible shape, and dropping unmatched parameters.
-
-
-
The coercion is useful to convert fully connected layers to their
-
equivalent convolutional layers, since the weights are the same and only
-
the shapes are different. In particular, equivalent fully connected and
-
convolution layers have shapes O x I and O x I x H x W respectively for O
-
outputs channels, I input channels, H kernel height, and W kernel width.
-
-
-
Both `net` to `new_net` arguments must be instantiated `caffe.Net`s.
-
"""
-
for p
in net.params:
#循环取出旧网络(例如VGG16网络)中每层的名字(用于两个网络间的匹配)
-
p_new = p + suffix
#将p+''赋值给p_new,目的是判断当前旧网络的该层所否也存在于新网络中
-
if p_new
not
in new_net.params:
#如果p所对应的层在新网络中没有,则直接丢弃
-
print
'dropping', p
-
continue
-
#net.params[p]一般有两项,且net.params[p][0]表示保存权重参数的数组,net.params[p][1]表示保存偏置的数组
-
for i
in range(len(net.params[p])):
-
if i > (len(new_net.params[p_new]) -
1):
#丢弃旧网络多余的参数,并退出当前for循环
-
print
'dropping', p, i
-
break
-
#如果新网络该层的参数形状与旧网络不同(参数的数目相同),则打印“强制转换”该层;否则打印“复制”该层参数
-
if net.params[p][i].data.shape != new_net.params[p_new][i].data.shape:
-
print
'coercing', p, i,
'from', net.params[p][i].data.shape,
'to', new_net.params[p_new][i].data.shape
#对于全连接层转换为全卷积层,需要进行参数强制转换
-
else:
-
print
'copying', p,
' -> ', p_new, i
-
#无论是强制转换还是复制操作,因为参数数目相同,所以可以直接平铺进行参数的赋值
-
new_net.params[p_new][i].data.flat = net.params[p][i].data.flat
此函数的最后一行new_net.params[p_new][i].data.flat = net.params[p][i].data.flat的理解可参见以下例子:
-
import numpy
as np
-
a = np.array([[[
1,
2,
3],[
4,
5,
6]],[[
7,
8,
9],[
10,
11,
12]],[[
13,
14,
15],[
16,
17,
18]]])
-
b=np.zeros([
6,
3])
-
b.flat=a.flat
-
print b
运行结果为:
-
[[
1.
2.
3.]
-
[
4.
5.
6.]
-
[
7.
8.
9.]
-
[
10.
11.
12.]
-
[
13.
14.
15.]
-
[
16.
17.
18.]]
利用此函数将VGG16模型的参数复制给FCN32s网络结果如下:
-
copying conv1_1 -> conv1_1
0
-
copying conv1_1 -> conv1_1
1
-
copying conv1_2 -> conv1_2
0
-
copying conv1_2 -> conv1_2
1
-
copying conv2_1 -> conv2_1
0
-
copying conv2_1 -> conv2_1
1
-
copying conv2_2 -> conv2_2
0
-
copying conv2_2 -> conv2_2
1
-
copying conv3_1 -> conv3_1
0
-
copying conv3_1 -> conv3_1
1
-
copying conv3_2 -> conv3_2
0
-
copying conv3_2 -> conv3_2
1
-
copying conv3_3 -> conv3_3
0
-
copying conv3_3 -> conv3_3
1
-
copying conv4_1 -> conv4_1
0
-
copying conv4_1 -> conv4_1
1
-
copying conv4_2 -> conv4_2
0
-
copying conv4_2 -> conv4_2
1
-
copying conv4_3 -> conv4_3
0
-
copying conv4_3 -> conv4_3
1
-
copying conv5_1 -> conv5_1
0
-
copying conv5_1 -> conv5_1
1
-
copying conv5_2 -> conv5_2
0
-
copying conv5_2 -> conv5_2
1
-
copying conv5_3 -> conv5_3
0
-
copying conv5_3 -> conv5_3
1
-
coercing fc6
0
from (
4096,
25088) to (
4096,
512,
7,
7)
-
copying fc6 -> fc6
1
-
coercing fc7
0
from (
4096,
4096) to (
4096,
4096,
1,
1)
-
copying fc7 -> fc7
1
-
dropping fc8
从中可以看出conv5_3之前的所有卷积层的权重和偏置参数是直接复制VGG16模型相对应层的参数的,而fc6和fc7层是进行了强制转化,将原来全连接层的权重参数强制赋值给了卷积层的卷积核参数,fc6和fc7的偏置仍旧采用直接复制的形式(其实强制转化和复制都是通过python的flat函数来完成的,本质是一样的,只是概念上加以区分而已)。
也可以从中看出为何FCN32s的fc6层的卷积核大小是7*7,为何fc7层卷积核的大小为1*1,目的就是为了使得强制转化前后参数的数目不变。
coercing fc6 0 from (4096, 25088) to (4096, 512, 7, 7)
其中,512*7*7=25088。
(2)upsample_filt()函数
-
#用于产生双线性核,来初始化反卷积层的卷积核权重参数
-
def upsample_filt(size):
-
"""
-
Make a 2D bilinear kernel suitable for upsampling of the given (h, w) size.
-
"""
-
factor = (size +
1) //
2
#//在python中是除号,但结果取整(向下取整)
-
if size %
2 ==
1:
-
center = factor -
1
-
else:
-
center = factor -
0.5
#center为插值中心点
-
og = np.ogrid[:size, :size]
#ogrid用于产生从0~(size-1)的两个序列(前者为列向量,后者为行向量)
-
#返回一个size×size大小的双线性核(除以factor是为了归一化,使得四个插值点的插值权重之和为1)
-
return (
1 - abs(og[
0] - center) / factor) * \
-
(
1 - abs(og[
1] - center) / factor)
拿size=4为例,该函数的运行结果如下:
-
[[
0.0625
0.1875
0.1875
0.0625]
-
[
0.1875
0.5625
0.5625
0.1875]
-
[
0.1875
0.5625
0.5625
0.1875]
-
[
0.0625
0.1875
0.1875
0.0625]]
双线性核是由双线性插值而来,但也不完全是双线性插值,在说明原理前,先放一张卷积及其反卷积的原理动图(上者为卷积过程,下者为对应的反卷积过程):
(注:双线性插值可参见https://blog.csdn.net/xbinworld/article/details/65660665)
从反卷积动图中可以看出,在反卷积前需要在输入图像(蓝色)的每一像素间进行补零,且补的零的维数是s-1(s为反卷积所对应的卷积过程的步长,即上者卷积动图中的步长为2,故下者反卷积过程每一像素间补了1维的0),且反卷积过程的步长是固定为1的。具体大家可以参见https://github.com/vdumoulin/conv_arithmetic
FCN中的upsample是通过反卷积实现的,假如上采样因子为2,即反卷积的步长为s=2(这个步长其实指的是反卷积所对应的逆过程即卷积过程中的步长,反卷积的步长固定为1),卷积核大小k=4。卷积核的权重初始化利用upsample_filt(k)得到,也即上述例子中的结果。大家可能会有疑惑,双线性插值是通过邻近的四个点进行插值的,但这卷积核有k*k个元素,即总共16个点进行插值(说白了就是16个点的加权求和),这也就是为何一开始要说明反卷积的实现过程了,从动图中可以看出输入图像每一像素间是有补零的,拿输入为3*3为例,其反卷积前需要进行补零,也即下图:
此时反卷积过程如下(蓝色的为原3*3的输入图像像素点,白色的为补零的点,灰色的为卷积核):
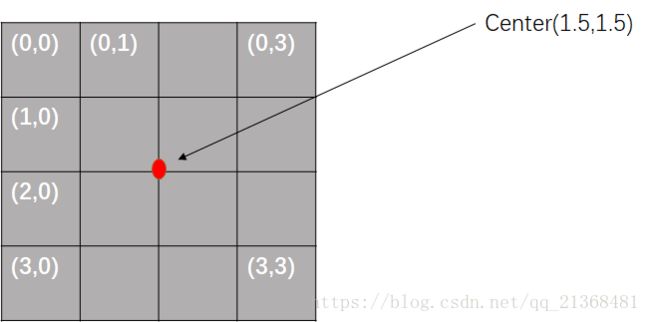
从上述反卷积过程中可以看出,卷积核内部最多只有输入图像的四个像素点(且这四个像素点所对应的卷积核所在位置的四个权重之和为1,也就对应了代码里的归一化操作),这也正是为何说双线性核是由双线性插值而来的,但又不完全是,原因在于其中的归一化操作,如下图所示:
其中,Center的坐标值即为upsample_filt()函数中的center;图中每个格中的白色数字即为每一格的坐标值,拿第二个格为例,其坐标为(0,1),则该位置所对应的权重为:
先从x轴方向开始:a=1-abs(1-center)/factor=1-abs(1-1.5)/2=0.75
再是y轴方向:b=1-abs(0-center)/factor=1-abs(0-1.5)/2=0.25
故最终的权重为:w=a*b=0.1875(也正是例子中第二个格所对应的权重)
此过程也即双线性插值过程,只是多了除以factor这一归一化操作,也就不是完全意义上的双线性插值了。
最后拿自己编写的C++程序来直观说明一下这个双线性核进行插值的效果,源代码如下:
-
#include
-
#include
-
#include
-
-
using
namespace
std;
-
using
namespace cv;
-
-
Mat kernel(int size)
-
{
-
int factor = (size +
1) /
2;
-
double center = factor -
0.5;
-
if (size %
2 ==
1)
-
center = factor -
1;
-
Mat tempk = Mat::zeros(size,
1,CV_32F);
-
for (
int i =
0; i < size; i++)
-
tempk.at<
float>(i,
0) =
1 -
abs(i - center)*
1.0 / factor;
-
Mat ker = Mat::zeros(size, size, CV_32F);
-
ker = tempk*tempk.t();
-
return ker;
-
}
-
int main()
-
{
-
Mat src=imread(
"image.jpg");
-
int col = src.cols,row=src.rows;
-
int k =
8, s =
4;
-
int outh = (row -
1)*s +
4;
-
int outw = (col -
1)*s +
4;
-
Mat result = Mat::zeros(outh, outw, CV_8UC3);
-
outh = outh -
1 + k;
-
outw = outw -
1 + k;
-
Mat dst = Mat::zeros(outh, outw, CV_8UC3);
-
for (
int i =
1; i < outh; i += s)
-
{
-
Vec3b* data1 = dst.ptr
(i);
-
Vec3b* data2 = src.ptr
(i/s);
-
for (
int j =
1; j < outw; j += s)
-
data1[j] = data2[j/s];
-
}
-
imwrite(
"卷积补零图.jpg", dst);
-
-
Mat mask = kernel(k);
//调用kernel()函数生成双线性核
-
-
for (
int i =
0; i < dst.rows-k+
1; i++)
-
{
-
Vec3b* data3 = result.ptr
(i);
-
for (
int j =
0; j < dst.cols-k+
1; j++)
-
{
-
for (
int s =
0; s < k; s++)
-
for (
int t =
0; t < k; t++)
-
{
-
data3[j](
0) += mask.at<
float>(s, t)*dst.at
(i + s, j + t)[
0];
-
data3[j](
1) += mask.at<
float>(s, t)*dst.at
(i + s, j + t)[
1];
-
data3[j](
2) += mask.at<
float>(s, t)*dst.at
(i + s, j + t)[
2];
-
}
-
}
-
}
-
-
imwrite(
"最终插值图.jpg", result);
-
-
waitKey();
-
return
0;
-
}
当反卷积核大小为k=8,步长为s=4时,结果如下(左上为原图,右上为卷积补零图(为了和原图放在同一行,进行了缩放,实际大小为1343*2007),下中为插值后的图像(也进行了缩放,实际大小为1336*2000)):
从上图可以看出,在放大倍数不大的情况下,使用双线性核进行插值得到的效果还是挺好的。
(3)interp()函数
-
#调用upsample_filt()函数进行反卷积核的权重赋值(初始化)
-
def interp(net, layers):
-
"""
-
Set weights of each layer in layers to bilinear kernels for interpolation.
-
"""
-
for l
in layers:
-
m, k, h, w = net.params[l][
0].data.shape
#net.params[l][0]为卷积核权重(不是偏置)
-
if m != k
and k !=
1:
#反卷积层但输入和输出图像数目应该是相同的,或者输出图像数目为1
-
print
'input + output channels need to be the same or |output| == 1'
-
raise
-
if h != w:
#卷积核需要是方形的
-
print
'filters need to be square'
-
raise
-
filt = upsample_filt(h)
#计算卷积核权重参数
-
#将filt赋值给每一卷积核,即反卷积层但每一卷积核但权重都一样,均为双线性插值初始化
-
net.params[l][
0].data[range(m), range(k), :, :] = filt
(4)expand_score()函数
-
#拓展score层,即将旧网络该层的参数移植到新网络上(注:新网络该层但分类数k<旧网络该层但分类数k')
-
def expand_score(new_net, new_layer, net, layer):
-
"""
-
Transplant an old score layer's parameters, with k < k' classes, into a new
-
score layer with k classes s.t. the first k' are the old classes.
-
"""
-
old_cl = net.params[layer][
0].num