伪C++开发小游戏---连连看

几个月之前就想要开发一个连连看小游戏，但是当时在算法这一步上面卡住了，之后也就不了了之。暑假末期将至，突然又想起了这个想法，正好这时候也有了一点思路，打了十几个小时终于最后做出了一个差不多的模样，写一篇笔记记录一下。

至于标题为什么写伪C++，主要是因为在开发过程中基本全是利用了C的思想，全程面向过程去开发，用到C++仅仅是几个STL函数。

最终的效果大致如下:

 前期准备

这里主要是关于两个相关的前期准备，一个是图形可视化库EasyX库的安装，然后是准备图案。

EasyX

首先开发一个小游戏需要一些图形化的界面，这里我用了easyx，需要一些文件的操作，可以搜索一下怎么下载，网上有很多资源 。

图案

对于消除图案的选择，这个可以随便定，动物植物都可以，在这里我选了水果，非常呆萌，图案的下载可以去iconfont-阿里巴巴矢量图标库，有许多矢量图资源。

对于消除线我整理之后大概有六种基本的线型，分别是竖线，横线，左上，左下，右上，右下。这个我是用的ppt制作之后直接截图，然后把背景扣掉了，截图的大小最好与上文的消除图案大小一致，为了后面统一修改大小，尽量对齐。我就没对齐，所以看起来还是有点别扭

修改好大小之后放到这个路径下，与对应项目的debug同级的。 

预热程序---番外篇

为什么叫番外篇，因为这一段其实是我研究一些算法用到的，并不是真正项目，但是后面的开发也基于这几个重要的程序，就是添枝加叶的问题，所以单独拉出来说一说。

判定消除

引入

连连看消除的规则非常简单，只要待消除的两个图案相同并且可以通过一个转弯不超过两次的折线连接便可以成功消除，基于这个原则，考虑将图案先简化为一个个点，形成一个点阵，这时候待消除的两个点可以视为是起点和终点，然后就是搜索路径。

搜索路径的方法有多种，主要分为深度优先搜索和广度优先搜索。因为转弯最多就两次，所以很多时候连线都是一条比较直的线，这很像是一直向前走的深度优先搜索，所以我就考虑用深度优先搜索。所以调了不知道多久

易混点

为了后面的程序统一性，这里取到的X轴Y轴是和EasyX的定义一致的，也就是X轴向右，Y轴向下，所以这时候的Y值其实是行值，X值其实是列值，对于矩阵 a [ ] [ ] ,xy分别是XY坐标，那么对应的点其实是a[y][x]。

还有一点因为连连看的连线是可以在游戏矩阵之外的，所以我在外面也扩充了一圈，这样的话在外面的就相当于也是迷宫中的路，同时因为扩充了之后第0行和0列都被占用了，所以这时候的真正游戏界面就是从1下标开始。

DFS寻找路径

起点设置为S，终点设置为T，我们需要的是还原路径，所以在过程中不仅需要记录坐标，还要记录是横线还是竖线（对应的就是上下走还是左右走），我是将其放在在栈中。

dfs递归搜索的过程中需要的参数分别是当前坐标，起点终点坐标，当前转弯的个数，方向参数，查找情况。

几个坐标好理解，需要注意的就是坐标都是对应的x值为列值；转弯次数就是从起点走到这个点走了多少步，为了记录，我单独开了一个flag数组来记录步数（一开始本来是用来标记访问的，后来发现没有必要），flag[i][j]表明的意思就是从起点(qdx,qdy)走到当前位置(j,i)的最小步数；方向参数好理解，就是方向，每个方向对应的是方向数组的索引，方向数组分为两个，一个对应x轴，一个对应y轴，也就是程序中的dirx和diry，一个索引对应两个dir值，分别加上当前的xy坐标值可以实现上下左右的移动，设置这个参数主要是为了可以让下一次的查找还是从这个方向开始，就可以实现一个类似于可以向前一直向前走的这样一个操作，当然需要注意的是不能反方向走，在遇到无效方向是要及时continue；还有一个参数是引用参数，是判断当前是否已经找到答案的，要是找到了，直接退出。

在后面程序的测试中发现可能还是存在一些bug，但是目前还不知道哪里存在问题，但是判定消除基本无误。

void dfs(int x,int y, int qdx, int qdy,int zdx,int zdy,int step,int now,int &stats) {
	if (stats)return;//找到了就不找了
	//判断,参数分别是x,y,(x向右,y向下),起点xy和终点xy,当前转弯次数,当前方向参数，0123分别是上右下左,当前寻找的状态
	if (step == 3) {//超出步数或者障碍物
		if (!st.empty()) {//拿出去
			st.pop();
		}
		return;
	}
	if (zdx==x&&zdy==y&&step <= 2) {//终点
		stats = 1;
		st.pop();//终点不需要变成横线
		return;
	}
	for (int i = now; i < now + 4; i++) {//从当前方向开始找
		int index = i % 4;
		int xx = x + dirx[index];
		int yy = y + diry[index];
		if (i == now + 2&&x!=qdx&&y!=qdy || xx < 0 || yy < 0 || xx == N || yy == N||
			mat[yy][xx]&&!(xx==zdx&&yy==zdy))//不合法,最后一个代表已经被占据并且不是终点
			continue;
		if (now == index|| x == qdx && y == qdy) {//方向相同或者是起点
			flag[yy][xx] = min(flag[y][x], flag[yy][xx]);//不需要加转弯次数
			st.push({ xx,yy ,i%2});//当前区块信息入栈
			dfs(xx, yy, qdx,qdy,zdx,zdy,step, index, stats);
		}
		else {
			flag[yy][xx] = min(flag[y][x] + 1, flag[yy][xx]);//需要加转弯次数
			st.push({ xx,yy,now%2 });
			dfs(xx, yy, qdx, qdy, zdx, zdy, step + 1, index, stats);
		}
		if (stats)return;
	}
	if (stats)return;
	if (!st.empty()) {//四个方向都没有
		st.pop();
	}
	return ;
}

矩阵生成

下面就是矩阵的生成，首先先把扩充后的点阵所有值初始化为0，0在后面就是代表空，也就是不显示。

因为要保证程序尽量可以消除，所以为了避免很多不能消除，我在生成时基于以下原则：先确定点种类数（1--cag），然后开始生成，随机找两个点，判定能否消除，如果可以，那么确定下来两个点对应都是当前这个种类的点，如果不能消除，那么计次，如果达到一百次，也就是找了一百组点都没找到可以消除的，那么认为当前已经到了生成的最大值，完成矩阵生成。这样做的好处就是每一组点都是基于可以消除生成的，所以解很比较多，而不至于很快就没有解。

int create_mat() {
	srand((unsigned)time(NULL));
	//生成N-2*N-2大小游戏矩阵,目前采用的算法是随机生成，可能最后不能填满...
	int max_num = (N - 2)*(N - 2);
	bool t[10000];
	for (int i = 0; i <= max_num + 1; i++)
		t[i] = 0;
	for (int i = 0; ;i++) {
		for (int now = 1; now <= cag; now++) {
			int epco = 0;
			while(1) {//最多循环100次,生成不了就算了
				int z1, z2;
				while (1) {
					z1 = rand() % max_num + 1;//找到两个没出现过的位置
					if (!t[z1]) {
						t[z1] = 1;
						break;
					}
				}
				while (1) {
					z2 = rand() % max_num + 1;
					if (!t[z2]) {
						t[z2] = 1;
						break;
					}
				}
				int x1 = (z1-1) % (N - 2)+1;
				int y1 = (z1 - 1) / (N - 2)+1;//计算行列
				int x2 = (z2-1) % (N - 2)+1;
				int y2 = (z2 - 1) / (N - 2)+1;

				int check = 0;
				ini_flag(y1,x1);
				dfs(x1, y1, x1, y1, x2, y2, 0,0,check);
				while (!st.empty())
					st.pop();
				//printf("%d %d %d %d %d\n", x1, y1, x2, y2, check);
				if (check) {//有解
					mat[y1][x1] = now;
					mat[y2][x2] = now;
					break;
				}
				else {//无解
					epco++;
					t[z1] = 0;
					t[z2] = 0;
				}
				if (epco == 100)break;
			}
			//printf("haha\n");
			//printf("i=%d now=%d epco=%d i * cag + now=%d\n", i, now, epco, i * cag + now);
			if (epco == 100 || i * cag + now == max_num/2) {
				return i * cag + now-(epco==100);//循环一百次还没找到答案或者数量达到了,返回生成的组数
			}
		}
	}
}

结果显示

如果要消除了就要显示消除的样子，下面就主要介绍怎么显示。我单独开辟了一个矩阵tmp来暂存点阵，然后将刚才dfs过程中找到的点统统标记为-1，这时候存在的点是正数，不存在的是0，而负数就代表了消除路线所经过的方块。遍历数组，判断点阵情况，正数就显示数字，0不显示，负数直接把路径经过的点记为'.'。

void show_mat(int mat[N][N]) {
	//for(int i=1;i<=N)
	printf("   ");
	for (int i = 1; i <= N - 2; i++)
		printf("%d ", i);
	printf("\n ");
	for (int i = 0; i < N ; i++)
	{
		if (i == N - 1)printf(" ");//调整最后一行点的格式
		if(i<=N-2&&i>=1)
			printf("%d", i);
		for (int j = 0; j < N ; j++) {
			if (mat[i][j] <0 ) {
				if(mat[i][j]==-1)
					printf(". ");//显示答案
				else
					printf(". ");//显示答案
			}
			else if (mat[i][j])
				printf("%d ", mat[i][j]);
			else
				printf("  ");//否则不显示
		}
		printf("\n");
	}
}

初级汇总

简单综合一下，加入一些用户交互，就可以实现一个非常简陋的数字点阵连连看，用户输入坐标实现选择。

下面是完整的代码

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#include
#include 
#include 
#include//图形绘制库
using namespace std;
const int N = 9+2; // 游戏界面加上隐藏一圈的大小,第一个数字是真正的游戏界面大小,1-9
const int cag = 9;//数字种类，1-9
const int inf = 0x3f3f3f3f;

int dirx[] = { 0,1,0,-1 };
int diry[] = { -1,0,1,0 };

struct node {
	int x,y,dir;//横坐标,纵坐标,方向(上下或者左右)
};

queueq;
stackst;

char a[N][N];
int flag[N][N];//次数
int mat[N][N];//游戏界面矩阵
int tmp[N][N];//暂存矩阵

void print() {
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++)
			printf("%c ", a[i][j]);
		printf("\n");
	}
}

void ini_flag(int x,int y) {//相当于x-行,y-列
	for (int i = 0; i < N; i++)
		for (int j = 0; j < N; j++) {
			flag[i][j] = inf;
		}
	flag[x][y] = 0;
}

void all_ini() {
	for (int i = 0; i < N; i++)
		for (int j = 0; j < N; j++) {
			mat[i][j] = 0;
		}
}

void show_mat(int mat[N][N]) {
	//for(int i=1;i<=N)
	printf("   ");
	for (int i = 1; i <= N - 2; i++)
		printf("%d ", i);
	printf("\n ");
	for (int i = 0; i < N ; i++)
	{
		if (i == N - 1)printf(" ");//调整最后一行点的格式
		if(i<=N-2&&i>=1)
			printf("%d", i);
		for (int j = 0; j < N ; j++) {
			if (mat[i][j] <0 ) {
				if(mat[i][j]==-1)
					printf(". ");//显示答案
				else
					printf(". ");//显示答案
			}
			else if (mat[i][j])
				printf("%d ", mat[i][j]);
			else
				printf("  ");//否则不显示
		}
		printf("\n");
	}
}

void dfs(int x,int y, int qdx, int qdy,int zdx,int zdy,int step,int now,int &stats) {
	if (stats)return;//找到了就不找了
	//判断,参数分别是x,y,(x向右,y向下),起点xy和终点xy,当前转弯次数,当前方向参数，0123分别是上右下左,当前寻找的状态
	if (step == 3) {//超出步数或者障碍物
		if (!st.empty()) {//拿出去
			st.pop();
		}
		return;
	}
	if (zdx==x&&zdy==y&&step <= 2) {//终点
		stats = 1;
		st.pop();//终点不需要变成横线
		return;
	}
	for (int i = now; i < now + 4; i++) {//从当前方向开始找
		int index = i % 4;
		int xx = x + dirx[index];
		int yy = y + diry[index];
		if (i == now + 2&&x!=qdx&&y!=qdy || xx < 0 || yy < 0 || xx == N || yy == N||
			mat[yy][xx]&&!(xx==zdx&&yy==zdy))//不合法,最后一个代表已经被占据并且不是终点
			continue;
		if (now == index|| x == qdx && y == qdy) {//方向相同或者是起点
			flag[yy][xx] = min(flag[y][x], flag[yy][xx]);//不需要加转弯次数
			st.push({ xx,yy });
			dfs(xx, yy, qdx,qdy,zdx,zdy,step, index, stats);
		}
		else {
			flag[yy][xx] = min(flag[y][x] + 1, flag[yy][xx]);//需要加转弯次数
			st.push({ xx,yy,now%2 });
			dfs(xx, yy, qdx, qdy, zdx, zdy, step + 1, index, stats);
		}
		if (stats)return;
	}
	if (stats)return;
	if (!st.empty()) {//四个方向都没有
		st.pop();
	}
	return ;
}

int create_mat() {
	srand((unsigned)time(NULL));
	//生成N-2*N-2大小游戏矩阵,目前采用的算法是随机生成，可能最后不能填满...
	int max_num = (N - 2)*(N - 2);
	bool t[10000];
	for (int i = 0; i <= max_num + 1; i++)
		t[i] = 0;
	for (int i = 0; ;i++) {
		for (int now = 1; now <= cag; now++) {
			int epco = 0;
			while(1) {//最多循环100次,生成不了就算了
				int z1, z2;
				while (1) {
					z1 = rand() % max_num + 1;//找到两个没出现过的位置
					if (!t[z1]) {
						t[z1] = 1;
						break;
					}
				}
				while (1) {
					z2 = rand() % max_num + 1;
					if (!t[z2]) {
						t[z2] = 1;
						break;
					}
				}
				int x1 = (z1-1) % (N - 2)+1;
				int y1 = (z1 - 1) / (N - 2)+1;//计算行列
				int x2 = (z2-1) % (N - 2)+1;
				int y2 = (z2 - 1) / (N - 2)+1;

				int check = 0;
				ini_flag(y1,x1);
				dfs(x1, y1, x1, y1, x2, y2, 0,0,check);
				while (!st.empty())
					st.pop();
				//printf("%d %d %d %d %d\n", x1, y1, x2, y2, check);
				if (check) {//有解
					mat[y1][x1] = now;
					mat[y2][x2] = now;
					break;
				}
				else {//无解
					epco++;
					t[z1] = 0;
					t[z2] = 0;
				}
				if (epco == 100)break;
			}
			//printf("haha\n");
			//printf("i=%d now=%d epco=%d i * cag + now=%d\n", i, now, epco, i * cag + now);
			if (epco == 100 || i * cag + now == max_num/2) {
				return i * cag + now-(epco==100);//循环一百次还没找到答案或者数量达到了,返回生成的组数
			}
		}
	}
}

void play(int all_num) {
	int x1, y1, x2, y2;
	while (all_num) {//只要还剩下
		printf("输入两个消除目标的坐标:");
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		if (mat[y1][x1] != mat[y2][x2]) {
			printf("请保证数字匹配\n");
			continue;
		}
		if (x1 == x2 && y1 == y2) {
			printf("不要输入同一个坐标\n");
			continue;
		}
		if (x1 > 0 && x1 <= N - 2 && y1 > 0 && y1 <= N - 2 && x2 > 0 && x2 <= N - 2 && y2 > 0 && y2 <= N - 2)
		{
			int check = 0;
			ini_flag(y1, x1);
			dfs(x1, y1, x1, y1, x2, y2, 0, 0, check);
			if (check) {
				for (int i = 0; i < N; i++)
					for (int j = 0; j < N; j++)
						tmp[i][j] = mat[i][j];
				while (!st.empty()) {
					//printf("%d %d\n", st.top().x, st.top().y);
					if(st.top().dir%2==0)
						tmp[st.top().y][st.top().x] = -1;//表示上下
					else
						tmp[st.top().y][st.top().x] = -2;//表示左右
					st.pop();
				}
				printf("成功消除,消除情况如下\n");
				show_mat(tmp);
				all_num--;
				if (!all_num) {
					printf("恭喜你通关了");
					break;
				}
				mat[y1][x1] = 0;
				mat[y2][x2] = 0;
				printf("当前状态\n");
				show_mat(mat);
				printf("\n");
			}
			else {
				printf("不合法消除，重新输入\n");
			}
		}
		else {
			printf("请输入正确的坐标范围(1-%d)\n", N - 2);
		}
	}
}

void find_error() {//调试用的
	mat[1][3] = 4;
	mat[3][3] = 4;
	mat[1][1] = 2;
	mat[2][1] = 2;
	mat[3][1] = 1;
	mat[1][2] = 3;
	mat[2][2] = 1;
	mat[3][2] = 3;
	show_mat(mat);
	int check = 0;
	ini_flag(1, 1);
	dfs(3, 1, 3,1, 3, 3, 0, 0, check);
	for (int i = 0; i < N; i++)
		for (int j = 0; j < N; j++)
			tmp[i][j] = mat[i][j];
	while (!st.empty()) {
		printf("%d %d\n", st.top().x, st.top().y);
		if (st.top().dir % 2 == 0)
			tmp[st.top().y][st.top().x] = -1;//表示上下
		else
			tmp[st.top().y][st.top().x] = -2;//表示左右
		st.pop();
	}
	show_mat(tmp);
}

int main() {
	//set(); //调试用
	all_ini();//初始化所有矩阵
	int all_num = create_mat();//生成矩阵
	show_mat(mat);
	play(all_num);
	return 0;
}

连连看---正式程序

下面是真正的连连看开发，开发工具是VS2017。

基于上面几个算法，其实项目大体的结构已经有了。首先是生成，每个图片的种类其实就是一个编号，背后就是数字矩阵，先用以上生成规则去生成数字矩阵，然后利用数字找到对应图片，放到相应位置，而这个位置取决于相应的数字矩阵下标。判定两张图片能否消除其实也是判定相应的数字矩阵的数字能否匹配。画出路径主要取决于搜索过程中的过程栈存储的路径信息，这里还是比较容易晕。

还需要加入的功能主要包括交互，显示模块和提示模块。我这里使用的交互方式是鼠标交互，一开始是用的键盘，然而体验并不好；计时连击和提示的加入，主要是为了提高游戏体验感。

常量和全局变量

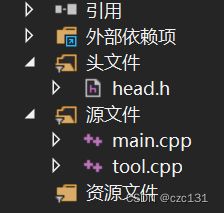
项目中会需要用到很多常数，为了方便查找最好放一起，我自己的项目结构如下，头文件head.h主要负责定义常量，一个主程序main.cpp定义入口，另一个tool.cpp则负责具体游戏的实现。

常量定义

const int N = 10 + 2; // 游戏界面加上隐藏一圈的大小,第一个数字是真正的游戏界面大小,1-6(当前适应大小)
const int cag = 7;//水果种类，1-7
const int inf = 0x3f3f3f3f;
#define SIZE 70 //图片尺寸
#define MAXX N*SIZE+400
#define MAXY N*SIZE
#define RIGHT 77
#define LEFT 75
#define UP 72
#define DOWN 80
#define ENTER 13
#define W 119
#define A 97
#define S 115
#define D 100
#define KONG 32
#define ESC 27//获取键值
#define EASY 130
#define NORMAL 90
#define DIFFICULT 70
#define DET 3 //连击间隔计算

 实现函数全局变量

/*全局变量*/
struct node {
	int x, y, dir;//横坐标,纵坐标,方向(上下或者左右)
};

int dirx[] = { 0,1,0,-1 };
int diry[] = { -1,0,1,0 };
stackst;//记录路径
IMAGE img[20];//存储图片
int all_num;//水果对数目
int rem_num;//消除个数
int flag[N][N];//次数,计算能否相连要用
int mat[N][N];//游戏界面矩阵,记录了每个位置的图片编号
int tmp[N][N];//暂存矩阵，标记线
//显示模块控制模块
clock_t start, stop;//clock_t为clock()函数返回的变量类型
double duration;//记录被测函数运行时间，以秒为单位
bool if_time;//标记是否计时
int max_num;//最高连击次数
int now_num;//当前连击次数
int k = (N - 2) / 2;//大小参数，为了调节不同大小适应的方阵距离
int kr=SIZE/5;//表示当前大小的方块对应的圆半径系数
int all_time;//可用初始时间
int time0;//游戏开始时间
int add_time = 1;//消除一个加1秒

初始化

作为一个项目，需要初始化的变量非常多，尤其是一些全局变量在一次游戏之内只需要初始化一次，最好把需要初始化的全部放到一个函数内封装起来，这样以后需要加入也会非常方便。

在这里我的初始化主要包括对于mat矩阵的清零操作，初始化一些全局变量，同时载入图片，放进图片数组。

/*初始化mat矩阵和图片以及计时模块*/
void all_ini() {
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			mat[i][j] = 0;
		}
	}
	if_time = 0;//一开始的不需要计时
	max_num = 1;
	now_num = 1;
	all_time = 100;
	time0 = time(0);
	loadimage(&img[1], "./imgs/西瓜.png");
	loadimage(&img[2], "./imgs/苹果.png");
	loadimage(&img[3], "./imgs/草莓.png");
	loadimage(&img[4], "./imgs/梨.png");
	loadimage(&img[5], "./imgs/火龙果.png");
	loadimage(&img[6], "./imgs/桃子.png");
	loadimage(&img[7], "./imgs/香蕉.png");
	loadimage(&img[10], "./imgs/竖线.png");
	loadimage(&img[11], "./imgs/横线.png");
	loadimage(&img[12], "./imgs/下右.png");
	loadimage(&img[13], "./imgs/下左.png");
	loadimage(&img[14], "./imgs/上右.png");
	loadimage(&img[15], "./imgs/上左.png");
}//初始化mat矩阵和图片

生成--判定--显示

生成和判定其实跟番外的那个是一样的，生成生成的还是数字，判定消除也是一样的，因为消除的虽然是图片，查找还是针对数字，没有任何变化，我自己也是直接复制了番外的代码，没做什么修改，就不多展开描述。 

生成图片部分略有变化，这时候针对传入的数组矩阵，如果是正数那么需要放入对应下标的图片，要记得乘上图片大小；如果是负数的话，那么就是路径点，分为多种情况，下文做考虑；如果是0那就是空，不显示。

用户操作

下面这里就是开发过程中的最大难点，也是联系最多程序的地方，也就是用户操作的编写，涉及到读取用户信息并处理。 

首先分析一下思路，用户面对一个连连看界面，会有两种操作，分别是键盘和鼠标的操作。

鼠标

首先是鼠标移动，也就是定位，然后选择水果并点击。

第一次选择时会在这个水果上面打上一个标记，同时状态转变（标记是第一个水果还是第二个水果的状态），在这之后可能会再点击，再次点击可能是空，也可能还是这个水果，这两种情况直接跳过，也就是判定为无效操作，同时清除标记，状态转变；再次点击还有可能是其他水果，这时候就要详细讨论，如下。

1.可以成功消除 

如果可以消除，那么这时候就要显示出消除线，同时清除两个水果，清除两个水果比较简单，只要在对应的数字矩阵中将对应位置的数字置为0，重新显示就是消除之后的样子，画出消除线相对复杂。

确定当前线now的方向需要前后两个矩阵元素信息，上面说了判定消除实际上可以返回一个栈，细化来看，这个栈实际上存储了从起点开始一直到终点的所有路径坐标以及对应的方向信息（也就是横线还是竖线），由于栈后进先出的的特点，一开始的栈顶实际上就是终点的方向信息，所以现在相当于是反恢复操作，将终点元素记录为bef（before），然后开始向下一个栈元素查找。观察下图可知，只有在前一个元素bef和自身元素now方向不相同时，这时才会有折线产生，而具体向哪边弯曲就取决于下一个元素，如果在上面，那就是向上折，向下就是向下折，而左右取决于bef元素在哪边，其他的各种情况同理，横线和竖线几乎相反，需要细分考虑，将所有情况都考虑到，然后给每个位置标上相应的线型编号，在显示时可以用到。

 在观察了这个图之后，发现可能还是放在队列中会更好恢复，直接从起点开始恢复，遇到当前线型和下一个不一样，就看下一个在哪边，就往哪边弯曲。

2.不能成功消除 

这种情况比较好考虑，考虑游戏的实际情况，这时候可以将标记点清除，切换回选第一个目标的状态。

键盘

然后是关于键盘的操作。关于键盘的操作可以有很多种，我主要设计了两种，分别是暂停和提示。

暂停非常好理解，就是点击了之后就会停止程序。下面介绍提示模块。

提示

关于提示，就是直接搜索数字矩阵，枚举寻找可以消除的数字，然后返回其坐标，利用画线函数将两个方块的路径标记好，显示出来，为了真实，我将其显示的时间设置为了1秒，然后就会消失，还可以加入次数限制，我还没有加入。

提示设计的难度不大，但是经过测试有时候可能难以达到实时水平，尤其是上面空旷的时候，由于搜索是优先向上，空旷就会导致搜索次数上升很快，导致卡顿，所以慎用。

显示模块

不同于前面的显示，这里的显示主要针对于一些游戏参数显示到屏幕上，比如连击信息，剩余时间，剩余数目等，同时还要考虑到全部消除和时间耗尽这两种结束显示。

连击和剩余数目

剩余数目很好理解，根据一般的游戏逻辑，连击就是上一次消除和这一次消除之间的间隔少于几秒再次消除就是连击，所以我们需要在上一次消除之后开始计时，然后等到再下一次消除看是否小于这个时间间隔，是那就给连击+1，否则重置连击数，这两个与消除息息相关，所以在每次成功消除之后调用该函数。

代码中的deal就是把一个数字转为字符串然后存到a中，因为outtextxy只能显示字符串。

/*计算和统计模块*/
void printCal() {
	char a[100];

	//计算连击
	settextcolor(WHITE);
	settextstyle(40, 40, 0);
	outtextxy(N*SIZE+40, 100, "当前连击");
	settextstyle(100, 100, 0);
	deal(now_num, a);
	outtextxy(N*SIZE+170, 200, a);

	//统计数目
	settextcolor(WHITE);
	settextstyle(30, 30, 0);
	outtextxy(N*SIZE+40, N*SIZE-250, "剩余水果对");
	settextstyle(100, 100, 0);
	deal(all_num, a);
	outtextxy(N*SIZE + 150, N*SIZE - 170, a);
}//计算连击和统计模块

剩余时间

剩余时间这里采纳了同学的建议，采用这样的计时方式：初始有一个时间长度，然后每次消除可以增加一定时间。

为了达到这样的效果，引入初始时间长度all_time，消除增加时间det_time和消除个数rem_num,同时记录开始时间time0，利用time(0)-time0即可得到从游戏开始到目前经过的时长，剩余时长可表达为下式:

all_time+(rem_num*det_time)-(time(0)-time0)

其中rem_num*det_time就是增加的时长，time(0)-time0就是游戏经过的时长。

这个需要一直更新，所以放在用户操作的主程序中调用。

/*打印时间*/
void printTime() {
	char a[100];
	//剩余时间
	settextcolor(WHITE);
	settextstyle(40, 40, 0);
	outtextxy(N*SIZE + 40, 300, "剩余时间");
	settextstyle(100, 100, 0);
	int t = all_time + (rem_num*add_time) - (time(0) - time0);
	deal(t, a);
	if (t % 10 == 9) {
		clearrectangle(N*SIZE + 170, 400, N*SIZE + 400, 500);
	}
	outtextxy(N*SIZE + 170, 400, a);
}//打印时间

游戏结束

游戏结束有两种情况，一种是时间耗尽，这种算是游戏失败，还有一种是全部消除，这种是游戏成功，成功的时候还可以打印出最高连击次数，比较简单，就不展开。

到这里程序主体完毕。

完整代码

head.h

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#include 
#include 
#include//图形绘制库
using namespace std;

const int N = 10 + 2; // 游戏界面加上隐藏一圈的大小,第一个数字是真正的游戏界面大小,1-6(当前适应大小)
const int cag = 7;//水果种类，1-7
const int inf = 0x3f3f3f3f;
#define SIZE 70 //图片尺寸
#define MAXX N*SIZE+400
#define MAXY N*SIZE
#define RIGHT 77
#define LEFT 75
#define UP 72
#define DOWN 80
#define ENTER 13
#define W 119
#define A 97
#define S 115
#define D 100
#define KONG 32
#define ESC 27//获取键值
#define EASY 130
#define NORMAL 90
#define DIFFICULT 70
#define DET 3 //连击间隔计算

void game();//游戏函数入口

 main.cpp

#include"head.h"
#include//图形绘制库

int main() {
	initgraph(MAXX + 1, MAXY + 1);
	game();
	return 0;
}

 tool.cpp

#include"head.h"
#include"conio.h"

/*全局变量*/
struct node {
	int x, y, dir;//横坐标,纵坐标,方向(上下或者左右)
};

int dirx[] = { 0,1,0,-1 };
int diry[] = { -1,0,1,0 };
stackst;//记录路径
IMAGE img[20];//存储图片
int all_num;//水果对数目
int rem_num;//消除个数
int flag[N][N];//次数,计算能否相连要用
int mat[N][N];//游戏界面矩阵,记录了每个位置的图片编号
int tmp[N][N];//暂存矩阵，标记线
//显示模块控制模块
clock_t start, stop;//clock_t为clock()函数返回的变量类型
double duration;//记录被测函数运行时间，以秒为单位
bool if_time;//标记是否计时
int max_num;//最高连击次数
int now_num;//当前连击次数
int k = (N - 2) / 2;//大小参数，为了调节不同大小适应的方阵距离
int kr=SIZE/5;//表示当前大小的方块对应的圆半径系数
int all_time;//可用初始时间
int time0;//游戏开始时间
int add_time = 1;//消除一个加1秒


/*初始化mat矩阵和图片以及计时模块*/
void all_ini() {
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			mat[i][j] = 0;
		}
	}
	if_time = 0;//一开始的不需要计时
	max_num = 1;
	now_num = 1;
	all_time = 30;
	rem_num = 0;
	time0 = time(0);
	loadimage(&img[1], "./imgs/西瓜.png");
	loadimage(&img[2], "./imgs/苹果.png");
	loadimage(&img[3], "./imgs/草莓.png");
	loadimage(&img[4], "./imgs/梨.png");
	loadimage(&img[5], "./imgs/火龙果.png");
	loadimage(&img[6], "./imgs/桃子.png");
	loadimage(&img[7], "./imgs/香蕉.png");
	loadimage(&img[10], "./imgs/竖线.png");
	loadimage(&img[11], "./imgs/横线.png");
	loadimage(&img[12], "./imgs/下右.png");
	loadimage(&img[13], "./imgs/下左.png");
	loadimage(&img[14], "./imgs/上右.png");
	loadimage(&img[15], "./imgs/上左.png");
}//初始化mat矩阵和图片


/*初始化flag*/
void ini_flag(int x, int y) {//相当于x-行,y-列
	for (int i = 0; i < N; i++)
		for (int j = 0; j < N; j++) {
			flag[i][j] = inf;
		}
	flag[x][y] = 0;
}//初始化flag

/*清除圆并补齐画面*/
void clearRound(int x,int y,int r,int detx,int dety) {//分别是xy点坐标，半径，偏移量
	int real_x, real_y;
	real_x = x * SIZE + SIZE / 2+detx;
	real_y = y * SIZE + SIZE / 2+dety;
	clearcircle(real_x, real_y, r);
	if(mat[y][x])
		putimage(x*SIZE, y*SIZE, &img[mat[y][x]]);//补上图片
}//清除圆并补齐画面

/*画一个圆*/
void drawRound(int x,int y,int r,int detx,int dety,int color){
	int real_x = x * SIZE + SIZE / 2;//圆心坐标
	int real_y = y * SIZE + SIZE / 2;
	circle(real_x + detx, real_y + dety, r);
	setfillcolor(color);  //填充色为蓝色
	fillcircle(real_x+detx, real_y +dety, r);
}//画一个圆

/*转换数字为字符串*/
void deal(int x, char *a) {
	stack sst;
	while (x) {
		sst.push(x % 10);
		x /= 10;
	}
	int l = 0;
	while (!sst.empty()) {
		a[l++] = sst.top() + '0';
		sst.pop();
	}
	a[l] = '\0';
	if (a[0] == '\0') {
		a[0] = '0';
		a[1] = '\0';
	}
}//转换数字为字符串

/*计算和统计模块*/
void printCal() {
	char a[100];

	//计算连击
	settextcolor(WHITE);
	settextstyle(40, 40, 0);
	outtextxy(N*SIZE+40, 100, "当前连击");
	settextstyle(100, 100, 0);
	deal(now_num, a);
	outtextxy(N*SIZE+170, 200, a);

	//统计数目
	settextcolor(WHITE);
	settextstyle(30, 30, 0);
	outtextxy(N*SIZE+40, N*SIZE-250, "剩余水果对");
	settextstyle(100, 100, 0);
	deal(all_num, a);
	outtextxy(N*SIZE + 150, N*SIZE - 170, a);
}//计算连击和统计模块

/*时间耗尽*/
void print_timeOver() {
	//打印时间耗尽
	settextcolor(BROWN);
	int size = k * 150 / (N - 2);//字体大小
	settextstyle(size, size, 0);
	outtextxy(N*SIZE / 2 - 4 * size, N*SIZE / 2 - 2 * size, "时间耗尽");
}//时间耗尽

/*打印时间*/
void printTime() {
	char a[100];
	//剩余时间
	settextcolor(WHITE);
	settextstyle(40, 40, 0);
	outtextxy(N*SIZE + 40, 300, "剩余时间");
	settextstyle(100, 100, 0);
	int t = all_time + (rem_num*add_time) - (time(0) - time0);
	deal(t, a);
	if (t % 10 == 9) {
		clearrectangle(N*SIZE + 170, 400, N*SIZE + 400, 500);
	}
	outtextxy(N*SIZE + 170, 400, a);
}//打印时间

/*结束*/
void printOver() {
	//打印消除完毕
	settextcolor(BROWN);
	int size = k*150 / (N - 2);//字体大小
	settextstyle(size, size, 0);
	outtextxy(N*SIZE/2-4*size, N*SIZE / 2 - 2*size, "全部消除");
	line(size, N*SIZE / 2 - size/2, N*SIZE - size, N*SIZE / 2 -  size/2);
	//打印最高连击
	char a[100];
	settextcolor(BLUE);
	size = k*90 / (N - 2);
	settextstyle(size, size, 0);
	outtextxy(N*SIZE / 2 -6 * size, N*SIZE / 2 , "最高连击次数");
	size = k*150 / (N - 2);
	settextstyle(size, size, 0);
	deal(max_num, a);
	outtextxy(N*SIZE / 2 -size/2, N*SIZE / 2+size, a);
	system("pause");
}//结束

/*打印当前状态*/
void show_mat(int Mat[N][N]) {
	printCal();
	line(N*SIZE, 0, N*SIZE, MAXY);
	for (int i = 0; i <= N - 1; i++) {
		for (int j = 0; j <= N - 1; j++) {
			if (Mat[i][j] < 0) {
				putimage(j*SIZE, i*SIZE, &img[-Mat[i][j]+9]);
			}
			else if (Mat[i][j] == 0)
				continue;
			else 
				putimage(j*SIZE, i*SIZE, &img[Mat[i][j]]);
		}
	}
}//打印当前状态

/*搜索答案*/
void dfs(int x, int y, int qdx, int qdy, int zdx, int zdy, int step, int now, int &stats) {
	if (stats)return;//找到了就不找了
	//判断,参数分别是x,y,(x向右,y向下),起点xy和终点xy,当前转弯次数,当前方向参数，0123分别是上右下左,当前寻找的状态
	if (step == 3) {//超出步数
		if (!st.empty()) {//拿出去
			st.pop();
		}
		return;
	}
	if (zdx == x && zdy == y && step <= 2) {//终点
		stats = 1;
		return;
	}
	for (int i = now; i < now + 4; i++) {//从当前方向开始找
		int index = i % 4;
		int xx = x + dirx[index];
		int yy = y + diry[index];
		if (i == now + 2 && x != qdx && y != qdy || xx < 0 || yy < 0 || xx == N || yy == N ||
			mat[yy][xx] && !(xx == zdx && yy == zdy))//不合法,最后一个代表已经被占据并且不是终点
			continue;
		if (now == index || x == qdx && y == qdy) {//方向相同或者是起点
			flag[yy][xx] = min(flag[y][x], flag[yy][xx]);//不需要加转弯次数
			st.push({ xx,yy,i % 2 });
			dfs(xx, yy, qdx, qdy, zdx, zdy, step, index, stats);
		}
		else {
			flag[yy][xx] = min(flag[y][x] + 1, flag[yy][xx]);//需要加转弯次数
			st.push({ xx,yy,i % 2 });
			dfs(xx, yy, qdx, qdy, zdx, zdy, step + 1, index, stats);
		}
		if (stats)return;
	}
	if (stats)return;
	if (!st.empty()) {//四个方向都没有
		st.pop();
	}
	return;
}//搜索答案

/*生成矩阵*/
int create_mat(int max_num) {
	srand((unsigned)time(NULL));
	//生成N-2*N-2大小游戏矩阵,目前采用的算法是随机生成，可能最后不能填满...
	bool t[10000];
	for (int i = 0; i <= max_num + 1; i++)
		t[i] = 0;
	for (int i = 0; ; i++) {
		for (int now = 1; now <= cag; now++) {
			int epco = 0,jh=0;
			while (1) {//最多循环100次,生成不了就算了
				int z1, z2;
				while (1) {
					z1 = rand() % max_num + 1;//找到两个没出现过的位置
					if (!t[z1]) {
						t[z1] = 1;
						break;
					}
				}
				while (1) {
					z2 = rand() % max_num + 1;
					if (!t[z2]) {
						t[z2] = 1;
						break;
					}
				}

				int x1 = (z1 - 1) % (N - 2) + 1;
				int y1 = (z1 - 1) / (N - 2) + 1;//计算行列
				int x2 = (z2 - 1) % (N - 2) + 1;
				int y2 = (z2 - 1) / (N - 2) + 1;

				int check = 0;
				ini_flag(y1, x1);
				dfs(x1, y1, x1, y1, x2, y2, 0, 0, check);
				while (!st.empty())
					st.pop();
				//printf("%d %d %d %d %d\n", x1, y1, x2, y2, check);
				if (check) {//有解
					mat[y1][x1] = now;
					mat[y2][x2] = now;
					break;
				}
				else {//无解
					epco++;
					t[z1] = 0;
					t[z2] = 0;
				}
				if (epco == 100 && t[z1] == 0) {
					jh = 1;//表示是退出的,而不是刚好在100轮生成
					break;
				}
			}
			if (jh || i * cag + now == max_num / 2- max_num%2) {
				show_mat(mat);
				return i * cag + now - jh;//循环一百次还没找到答案或者数量达到了,返回生成的组数
			}
		}
	}
}//生成矩阵

/*标记线*/
void deal(int x1,int x2,int y1,int y2) {
	for (int i = 0; i < N; i++)
		for (int j = 0; j < N; j++)
			tmp[i][j] = mat[i][j];//复制矩阵
	int bef_dir = st.top().dir;//初始方向
	int bef_x = st.top().x;
	int bef_y = st.top().y;
	st.pop();//终点不需要变成线
	while (!st.empty()) {
		int xx = st.top().x;
		int yy = st.top().y;
		int dir = st.top().dir;
		st.pop();
		if (dir == 0) {//上下
			//tmp[st.top().y][st.top().x] = -1;//表示上下
			if (bef_dir==dir) {
				//跟上一个一样
				tmp[yy][xx] = -1;//上下
			}
			else {         //左右
				if (!st.empty() && st.top().y < yy || st.empty() && y1 < yy) {
					//跟下一个比定上下,此时是下一个在上面
					if (xx < bef_x)//向左走
						tmp[yy][xx] = -5;//上右
					else
						tmp[yy][xx] = -6;//上左
				}
				else {
					if (xx < bef_x)//向左走
						tmp[yy][xx] = -3;//下右
					else
						tmp[yy][xx] = -4;//下左
				}
			}
		}
		else {
			//tmp[st.top().y][st.top().x] = -2;//表示左右
			if (bef_dir == dir) {//也是左右
				tmp[yy][xx] = -2;
			}
			// x1 y1 是起点坐标
			else {
				if (!st.empty() && st.top().x < xx || st.empty() && x1 < xx) {//下一个在左边
					if (yy < bef_y) //向上走
						tmp[yy][xx] = -4;//下左
					else 
						tmp[yy][xx] = -6;//上左
				}
				else {
					if (yy < bef_y)//向上走
						tmp[yy][xx] = -3;//下右
					else
						tmp[yy][xx] = -5;//上右
				}
			}
		}
		bef_x = xx;
		bef_y = yy;
		bef_dir = dir;//更新表示上一个状态的量
	}
}//标记线

/*处理消除之后的样子以及计时模块*/
bool deal_after(int x1,int x2,int y1,int y2) {
	//计时模块
	rem_num++;
	all_num--;
	if (if_time) {
		stop = clock();//停止计时
		duration = (double)(stop - start) / CLOCKS_PER_SEC;//计算运行时间
		if (duration <= DET) {
			now_num += 1;
			max_num = max(max_num, now_num);
		}
		else {
			now_num = 1;//重置连击次数
		}
	}
	//下面显示出消除的样子
	show_mat(tmp);
	Sleep(300);//程序暂停
	mat[y1][x1] = 0;
	mat[y2][x2] = 0;
	cleardevice();
	show_mat(mat);
	if (!all_num) {
		return 1;//代表可以结束游戏了
	}
	start = clock();//开始计时
	if_time = 1;//计时标记
	return 0;
}

/*提示模块*/
bool remind(int &x1, int &y1, int &x2, int &y2) {//返回是否可以消除,返回值内包括起点终点坐标
	for (int i1 = 1; i1 < N - 1; i1++) {
		for (int j1 = 1; j1 < N - 1; j1++) {
			if (!mat[i1][j1])
				continue;//空格
			for (int i2 = 1; i2 < N - 1; i2++) {
				for (int j2 = 1; j2 < N - 1; j2++) {
					if (!mat[i2][j2] || i1 == i2 && j1 == j2||mat[i2][j2]!=mat[i1][j1])
						continue;
					int check = 0;
					dfs(j1, i1, j1, i1, j2, i2, 0, 0, check);
					if(check) {
						x1 = j1;
						y1 = i1;
						x2 = j2;
						y2 = i2;
						return 1;
					}
					else {
						while (!st.empty())//否则要清空栈
							st.pop();
					}
				}
			}
		}
	}
	return 0;
}//提示模块

/*游戏操作部分*/
void play() {
	int x1=1, y1=1, x2=1, y2=1,now=1;//记录当前位置(x2,y2)和上一个位置(x1,y1),now记录当前状态，1是第一个，2是第二个
	int bef_t = time(0)-time0;
	while (all_num) {//只要还剩下
		MOUSEMSG m;
		if (bef_t != time(0) - time0) {
			printTime();
		}
		printTime();//打印时间
		if (all_time + (rem_num*add_time) - (time(0) - time0)==0) {//时间耗尽
			print_timeOver();
			system("pause");
		}
		if (MouseHit())//是否有鼠标消息
		{
			m = GetMouseMsg();
			if (m.uMsg == WM_LBUTTONDOWN)//左键
			{
				//rectangle(m.x - 5, m.y - 5, m.x + 5, m.y + 5);
				if (m.x > N*SIZE || m.y > N*SIZE)
					continue;
				m.x = m.x / SIZE;
				m.y = m.y / SIZE;
				if (now == 1) {//第一个确定状态只要不越界都可以,然后记录上一个位置
					x1 = m.x;
					y1 = m.y;//x1，y1存储上一次状态
					if (!mat[y1][x1])
						continue;//空格无效
					drawRound(x1, y1, kr, 0, 0, GREEN);
					now = 2;
				}
				else {//第二个要判定状态
					x2 = m.x;
					y2 = m.y;
					if (mat[y1][x1] != mat[y2][x2] || x1 == x2 && y1 == y2) {
						clearRound(x1, y1, kr, 0, 0);//重新选择
						now = 1;
						continue;
					}
					if (x1 > 0 && x1 <= N - 2 && y1 > 0 && y1 <= N - 2 && x2 > 0
						&& x2 <= N - 2 && y2 > 0 && y2 <= N - 2) {
						int check = 0;
						ini_flag(y1, x1);
						dfs(x1, y1, x1, y1, x2, y2, 0, 0, check);
						if (check) {
							deal(x1, x2, y1, y2);//标记线
							bool if_over = deal_after(x1, x2, y1, y2);//判断是否结束，同时善后工作
							if (if_over) {
								printOver();//打印结束语句
							}
						}
						else {
							clearRound(x1, y1, kr, 0, 0);//不能消除
							while (!st.empty())//清空栈
								st.pop();
						}
					}
					now = 1;
				}
			}
		}
		if (_kbhit()) {//如果有按键
			int ch = _getch();
			if (ch == KONG) {//提示按钮
				int check = remind(x1,y1,x2,y2);
				if (check) {
					deal(x1, x2, y1, y2);//标记线
					show_mat(tmp);
					Sleep(1000);
					cleardevice();
					show_mat(mat);
				}
			}
			else if (ch == ESC) {//暂停
				system("pause");
			}
		}
	}
}//游戏操作部分

/*总控程序*/
void game() {
	all_ini();//初始化所有矩阵和图片库
	all_num = create_mat((N - 2)*(N - 2));//生成矩阵
	show_mat(mat);
	play();
}//总控程序

总结

程序本身还有许多很多可以改进的地方，比如有时候显示消除线会错位，都到这个份上了还有什么好修改的，有时间还是需要修改一下，还有在遇到无法消除时的刷新，同时还想加入一些类似于关卡的模式，等有空再说吧。