吃瓜教程 | Datawhale-2021.10打卡（Task05）

第6章 支持向量机

6.1 间隔与支持向量

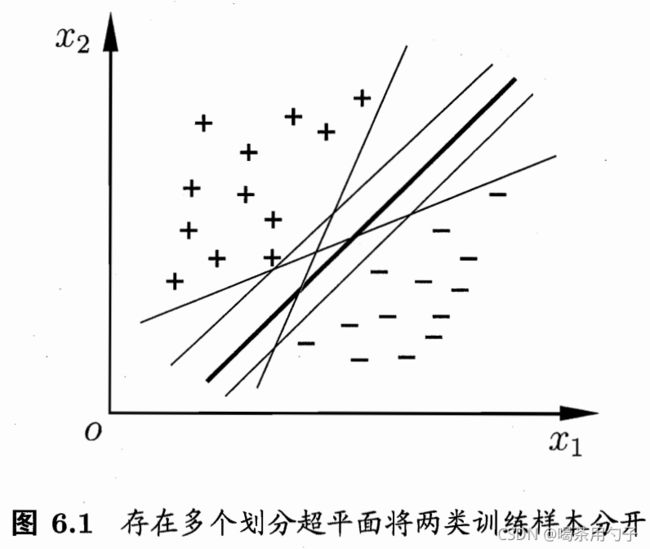
给定一组线性可分的训练样本，分类学习的目的就是找到一个划分超平面，将不同类别的样本分开，但根据前5章的知识可知，每次训练得到的超平面可能都不相同，如下图所示

因此，支持向量机的作用：从几何角度出发，对于线性可分数据集，支持向量机就是找距离正负样本都最远的超平面。相比于感知机，这个超平面的唯一的，且这个划分超平面所产生的分类结果是最鲁棒的，对未见示例的泛化能力最强。

样本空间中任易点$\mathbf{x}$到超平面$(\mathbf{\omega },b)$的距离可写为：

$$r=\frac{|{\mathbf{\omega }}^{\mathrm{T}}\mathbf{x}+b|}{\Vert \mathbf{\omega }\Vert }\text{\hspace{1em}(6.2)}$$

对于式(6.2)的证明过程如下所示：

支持向量机（Support Vector Machine，简称SVM）的基本模型如下：

$$\begin{array}{r}\{\begin{array}{l}\underset{\mathbf{\omega },b}{\min }\frac{1}{2}\Vert \mathbf{\omega }{\Vert }^2\\ \mathrm{s}.\mathrm{t}.y_i({\mathbf{\omega }}^{\mathrm{T}}{\mathbf{x}}_i+b)\ge 1,i=1,2,\dots ,m\end{array}\end{array}\text{\hspace{1em}(6.6)}$$

6.2 对偶问题

支持向量机（6.6）的对偶问题如下所示：

$$\begin{array}{rl}\underset{\mathbf{\alpha }}{\max }& \sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j\\ & \mathrm{s}.\mathrm{t}.\sum _{i=1}^m{\alpha }_i{y}_i=0,\\ & {\alpha }_i\ge 0,i=1,2,\dots ,m\end{array}\text{\hspace{1em}(6.11)}$$

将支持向量机原问题转化为拉格朗日对偶问题求解主要有如下两个原因：

1. 无论原问题是否为凸优化问题，对偶问题恒为凸优化问题，因为对偶函数恒为凹函数（加负号即可转化为凸函数）。而且原始问题的时间复杂度与特征维数成正比（若特征维数大，会导致出现维数灾难问题），而对偶问题和数据量成正比，当特征维数远高于数据量的时候，采用拉格朗日对偶问题求解更高校；
2. 对偶问题能引入核函数，进而可推广到非线性分类问题。（最主要的原因）

6.4 软间隔与正则化

上述两小节只考虑样本为线性可分情形，而在现实任务中，线性不可分的情形才是最常见的，由此引出了软间隔。

从数学角度出发，软间隔就是允许部分样本不满足下式中的约束条件：

$$\begin{array}{r}\{\begin{array}{l}\underset{\mathbf{\omega },b}{\min }\frac{1}{2}\Vert \mathbf{\omega }{\Vert }^2\\ \mathrm{s}.\mathrm{t}.y_i({\mathbf{\omega }}^{\mathrm{T}}{\mathbf{x}}_i+b)\ge 1,i=1,2,\dots ,m\end{array}\end{array}$$

在最大化间隔的同时，不满足约束的样本尽可能少。于是软间隔的优化目标可写为：

$$\underset{\mathbf{\omega },b}{\min }\frac{1}{2}\Vert \mathbf{\omega }{\Vert }^2+C\sum _{i=1}^m{\ell }_{0/1}(y_i({\mathbf{\omega }}^{\mathrm{T}}{\mathbf{x}}_i+b)-1)\text{\hspace{1em}(6.29)}$$

其中$C>0$是一个可人为调节的参数，${\ell }_{0/1}$是“0/1损失函数”

$${\ell }_{0/1}=\{\begin{array}{l}1,ifz<0;\\ 0,otherwise.\end{array}\text{\hspace{1em}(6.30)}$$

由上式可知，当满足约束条件时，损失为0；不满足约束条件时，损失不为0。
当C取$+\infty$时，为最小化目标函数式(6.29)，会迫使所有样本满足上述约束条件，进而导致所有样本的损失为0，使得软间隔问题退化为硬间隔问题。当C取有限值时，则允许一些样本不满足约束条件。

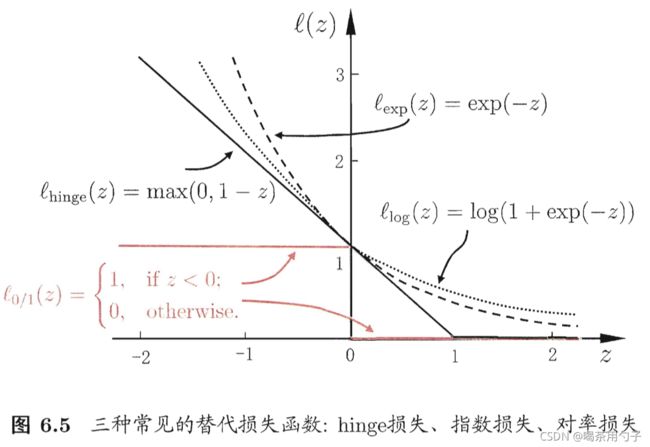
${\ell }_{0/1}$非凸、非连续、存在不可导的点，因此常用如下三种常用的替代损失函数：

• hinge损失：${\ell }_{hinge}(z)=\mathrm{m}\mathrm{a}\mathrm{x}(0,1-\mathrm{z})$;
• 指数损失（exponential loss）：${\ell }_{exp}(z)=\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{z})$;
• 对率损失（logistic loss）：${\ell }_{log}(z)=\mathrm{l}\mathrm{o}\mathrm{g}(1+\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{z}))$;

6.5 支持向量回归

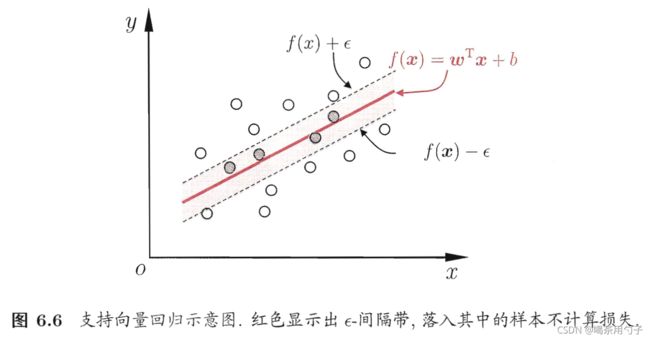
相比于线性回归用一条线来拟合训练样本，支持向量回归（Support Vector Regression，简称SVR）而是采用一个以$f(\mathbf{x})={\mathbf{\omega }}^{\mathrm{T}}\mathbf{x}+b$为中心，宽度为$2ϵ$的间隔带，来拟合训练样本。

落在间隔带内的样本不计算损失，在间隔带外的样本则以偏离带子的距离作为损失，然后以最小化损失的方式迫使间隔带从样本最密集的地方（中心地带）穿过，进而达到拟合训练样本的目的。

参考文献

-《机器学习》，周志华著，清华大学出版社.

-《南瓜书》，Datawhale，南瓜书链接.