LSTM原理专项介绍
LSTM提出背景
LSTM缓解了RNN中梯度消失的问题,使其可以处理长短时序列。但是LSTM并没有彻底解决梯度消失的问题。LSTM被各大科技公司应用在文字翻译,语音识别等方向,因为其相比RNN,在各个应用场景上带来了比较大的效果提升。
LSTM经过千锤百炼才有了现在的形态,so,让我们开始一睹芳容吧!
以下所有内容,如有侵权,请联系删除~
LSTM网络结构简介
由于RNN和LSTM都是循环神经网络,二者具有一定的相似,所以几乎所有的教程都会从RNN过渡到LSTM。在这里我们将简单看一下RNN的原理,然后快速过渡到LSTM。如需详细了解RNN,请点击:RNN原理介绍。
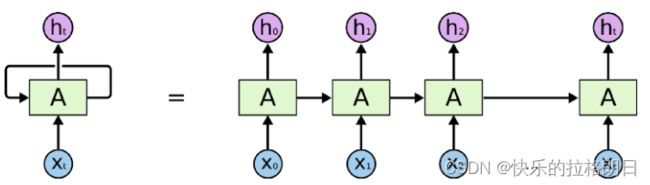
这是RNN经典的结构图,上图左边表示的是只有一层隐层的RNN网络,在时间轴上展开后得到右图。所谓RNN循环神经网络就是在时间轴上A的权值共享和循环利用。没错,在时间步上所有的A都是同一个东西,记住这一点!
时间轴可以是不同的对象,比如音频t秒为一帧,一帧就是一个时间步,RNN就是利用相同的权重去计算一段音频的不同帧,然后再输出;再比如视频t秒提取一个特征,同样这一个特征也是一个时间步,一段视频的多个特征组合成一个时间步序列;再比如一个样本提取一个特征,指定n个样本作为时间序列,那这个时间步的长度就为n……
只要合理,可以指定任何维度为时间步。
相比RNN,LSTM增加了一个单元状态 C t C^t Ct (cell state),此外还有和RNN名义上一样的隐状态变量 h t h^t ht (hidden state);并且LSTM对节点A进行了优化升级,在A里面增加了输入门,遗忘门,输出门这三个门机制,处理流程相比RNN复杂了很多。可以看出LSTM只是对隐层节点A做了改进,并增加了一个输入。但时间步循环的整体思路和结构不变,与RNN类似。
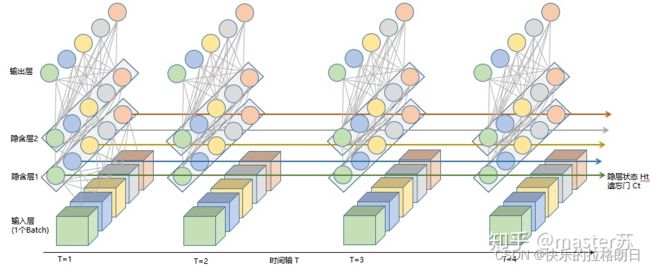
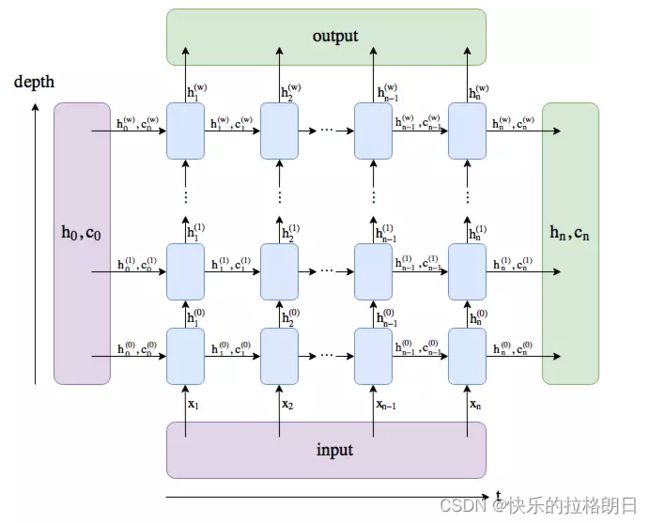
可以通过图片直观的感受不同时间步的网络状态,下图表示包含2个隐藏层的LSTM/RNN网络,也就是两个LSTM/RNN进行堆叠。在T=1时刻看,它是一个普通的BP网络,在T=2时刻看也是一个普通的BP网络。但是T时刻训练的隐藏层信息HC会被传递到下一个时刻T+1。这是LSTM和RNN循环的原理,也是与常规卷积网络的不同之处。
从下图直观感受,LSTM或者RNN在循环时变成了一个网络矩阵,但实际上这个网络只有最左边这一排的东西,右边三排是为了更容易理解时间步循环而画出来的。也就是说不同时间步上的网络都是同一组权重。比如下图中的T=1,T=2,….时的网络都是相同的,只不过不同时刻的输入和输出不相同。
遗忘门,输入门,输出门
了解LSTM时间步循环的原理后,就开始看一下LSTM内部的处理流程,整个LSTM内部流程可以分为三步:
- 利用输入 X t X_t Xt和上一时刻的隐状态信息 H t − 1 H_{t-1} Ht−1生成三个门控信息和一个候选记忆:遗忘门 F t F_t Ft,输入门 I t I_t It,输出门 O t O_t Ot,候选记忆 C ~ t \widetilde C_t C t;
- 遗忘门控制遗忘多少历史记忆 C t − 1 C_{t-1} Ct−1,输入门控制往历史记忆 C t − 1 C_{t-1} Ct−1中添加多少候选记忆 C ~ t \widetilde C_t C t。遗忘后的记忆加上选择后的记忆更新成新的记忆状态 C t C_t Ct;
- 输出门控制多少新的记忆状态成为隐状态 H t H_t Ht。新的记忆和隐状态为当前时刻的输出。
LSTM相当于一个工厂,里面包含了各种组件,各种组件支撑着LSTM的运行。这一小节将讲一下LSTM的各种组件。
首先想一下,为什么要在LSTM里面大费周章添加门机制呢?
这是因为门机制极大的减轻了梯度消失问题,简化了我们的调参复杂度。同时门机制提供了特征过滤,将有用的特征保存,没用的特征丢弃,这极大的丰富了向量的表示信息。至于为什么减轻了梯度消失问题,后面将讲到,在此之前先看一下各个关键的组件。
首先解释一下用到的符号
H t H_{t} Ht:t 时刻的隐状态。在 0 − t 0-t 0−t时刻的全局信息的影响下, 当前时刻的上下文表示。
X t X_t Xt:t 时刻的输入向量。
C t C_t Ct:t 时刻的记忆。本质上是 0 − t 0-t 0−t 时刻的全局信息。
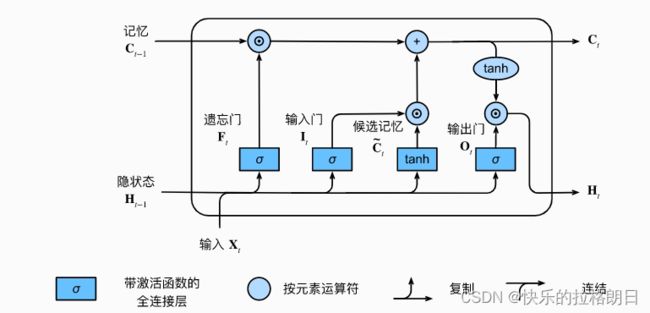
下图是比较经典的LSTM内部原理图,将以下图作为基础进行逐步拆解。下图 ’按元素运算符‘ 的意思是矩阵中对应的元素相乘,因此要求两个相乘矩阵是同型的
遗忘门
作用:控制保留多少过去的 C t − 1 C_{t-1} Ct−1记忆。选择性忘记,记住重要的,忘记不重要的
F t = σ ( W f ⋅ [ H t − 1 , X t ] + b f ) ( 1 ) F_t=\sigma(W_f·[H_{t-1},X_{t}]+b_f) \qquad(1) Ft=σ(Wf⋅[Ht−1,Xt]+bf)(1)
输入门
作用:选择记忆。采用多少来自tanh( C ~ t \widetilde C_t C t)的数据,选择一部分记忆,并把这部分加入到新的记忆中去,完成记忆的更新。
I t = σ ( W i ⋅ [ H t − 1 , X t ] + b i ) ( 2 ) I_t=\sigma(W_i·[H_{t-1},X_{t}]+b_i) \qquad(2) It=σ(Wi⋅[Ht−1,Xt]+bi)(2)
I t I_t It和 F t F_t Ft的作用类似,都是对一段记忆进行选择性的提取,并更新为新的记忆。不同的是 F t F_t Ft是对历史记忆进行选择; I t I_t It是对当前信息进行选择,选择的信息成为记忆中的一部分。
输出门
作用:决定 C t C^t Ct中哪些会被当成当前状态输出。在对 C t C_t Ct进行输出选择之前, C t C_t Ct首先经过tanh变换进行缩放。
O t = σ ( W o ⋅ [ H t − 1 , X t ] + b o ) ( 3 ) O_t=\sigma(W_o·[H_{t-1},X_t]+b_o) \qquad(3) Ot=σ(Wo⋅[Ht−1,Xt]+bo)(3)
候选记忆 C t C_t Ct
候选记忆是对两个输入非线性变换获得。
C t = t a n h ( W c [ H t − 1 , X t ] + b c ) ( 4 ) C_t=tanh(W_c[H_{t-1},X_t]+b_c) \qquad(4) Ct=tanh(Wc[Ht−1,Xt]+bc)(4)
当前单元状态
作为下一时间步的输入,保存了1-t所有的记忆
C t = F t ο C t − 1 + I t ο t a n h ( W c ⋅ [ H t − 1 , X t ] + b c ) ( 5 ) C_t=F_{t}\ \omicron \ C_{t-1}+I_t\ \omicron \ tanh(W_c·[H_{t-1},X_t]+b_c)\qquad(5) Ct=Ft ο Ct−1+It ο tanh(Wc⋅[Ht−1,Xt]+bc)(5)
输出隐藏层
每一个时间步的最后一层LSTM都将作为最终结果输出。
H t = t a n h ( C t ) ο O t ( 6 ) H_t=tanh(C_t)\ \omicron\ O_t \qquad(6) Ht=tanh(Ct) ο Ot(6)
以上一些关键组件和步骤都介绍完了,可能你还有疑问,比如上一时刻的隐状态信息 H t − 1 H_{t-1} Ht−1和样本输入 X t X_t Xt利用中括号括在一起是什么意思?为什么有的激活函数用sigmod,有的激活函数用tanh,这其中有什么讲究吗?LSTM内部可以使用正则化吗?还有是如何缓解了RNN的梯度消失?
对于第一个问题,其实是比较简单的。上一时刻的隐状态信息 H t − 1 H_{t-1} Ht−1和样本输入 X t X_t Xt利用中括号括在一起,是表示这两个信息拼接在一起,如何拼接?就是串接在一起。
激活函数的选择
在LSTM中,遗忘门、输入门和输出门使用 Sigmoid函数作为激活函数;在生成候选记忆时,使用双曲正切函数tanh作为激活函数。
为什么使用sigmod或者tanh?
门控信号越接近1,代表”记忆“下来的数据越多;而越接近0则代表”遗忘“的越多。Sigmoid的输出在0-1之同,符合门控的物理定义,且当输入较大或较小时,其输出会非常接近1或0,从而保证该门开或关,在生成候选记亿时;相比于relu,relu为0-+inf,无法表示记住的大小。
使用tanh函数,是因为其输出在-1,1之间,这与大多数场景下特征分布是0中心的吻合。此外,tanh函数在输入为0近相比 Sigmoid函数有更大的梯度,通常使模型收敛更快。
LSTM是如何缓解梯度消失的
根据RNN梯度消失的原因可以知道会存在中间状态的连乘。
类似RNN,研究一下 ∂ C t ∂ C t − 1 \partial C_t \over \partial C_{t-1} ∂Ct−1∂Ct:
根据链式求导法则以及上面六个公式可以进行展开:
∂ C t ∂ C t − 1 = ∂ C t ∂ f t ⋅ ∂ f t ∂ H t − 1 ⋅ ∂ H t − 1 ∂ C t − 1 + ∂ C t ∂ i t ⋅ ∂ i t ∂ H t − 1 ⋅ ∂ H t − 1 ∂ C t − 1 + ∂ C t ∂ C ~ t ⋅ ∂ C ~ t ∂ H t − 1 ⋅ ∂ H t − 1 ∂ C t − 1 + ∂ C t ∂ C t − 1 {\partial C_t \over \partial C_{t-1}} = {\partial C_t \over \partial f_t}·{\partial f_t \over \partial H_{t-1}}·{\partial H_{t-1} \over \partial C_{t-1}}+{\partial C_t \over \partial i_t}·{\partial i_t \over \partial H_{t-1}}·{\partial H_{t-1} \over \partial C_{t-1}}+{\partial C_t \over \partial \widetilde C_t}·{\partial \widetilde C_t\over \partial H_{t-1}}·{\partial H_{t-1} \over \partial C_{t-1}}+{\partial C_t \over \partial C_{t-1}} ∂Ct−1∂Ct=∂ft∂Ct⋅∂Ht−1∂ft⋅∂Ct−1∂Ht−1+∂it∂Ct⋅∂Ht−1∂it⋅∂Ct−1∂Ht−1+∂C t∂Ct⋅∂Ht−1∂C t⋅∂Ct−1∂Ht−1+∂Ct−1∂Ct
∂ C t ∂ C t − 1 = C t − 1 ⋅ σ ′ ⋅ W f ⋅ t a n h ′ ( C t − 1 ) ⋅ O t − 1 + C ~ t ⋅ σ ′ ⋅ W i ⋅ O t − 1 t a n h ′ ( C t − 1 ) + i t ⋅ t a n h ′ ( ⋅ ) ⋅ W c ⋅ O t − 1 ⋅ t a n h ′ ( C t − 1 ) + f t {\partial C_t \over \partial C_{t-1}} = C_{t-1}·\sigma'·W_f·tanh'(C_{t-1})·O_{t-1}+\widetilde C_t·\sigma'·W_i·O_{t-1}tanh'(C_{t-1})+i_t·tanh'(·)·W_c·O_{t-1}·tanh'(C_{t-1})+f_t ∂Ct−1∂Ct=Ct−1⋅σ′⋅Wf⋅tanh′(Ct−1)⋅Ot−1+C t⋅σ′⋅Wi⋅Ot−1tanh′(Ct−1)+it⋅tanh′(⋅)⋅Wc⋅Ot−1⋅tanh′(Ct−1)+ft
从上述推导中可以看出,Cell连乘部分是个加项,而 f t , i t , o t , C ~ t f_t,i_t,o_t,\widetilde C_t ft,it,ot,C t都是神经网网络自己学到的,因此可以通过学习改变门控的值,使梯度维持在合理的范围内。加项使得梯度传递更为恰当。当然梯度可以大于1也可以小于1,至于到底取什么值,这完全由神经网络根据自己学到的门控权值决定。
总结来说就是,RNN的前一个记忆对后一个记忆的导数是常数,这样RNN的某个偏导数一直都是大于1或者在[0,1]之间,这样会导致梯度消失或者爆炸。而LSTM的导数是可以改变的,在每个时刻都是可以大于1或者在[0,1]区间之内的。
但是LSTM并没有彻底解决梯度的问题,文献记载,在序列过长的情况下,仍然可能会出现梯度消失的问题。
tensorflow API中的dropout正则化
LSTM(100, dropout=0.2, recurrent_dropout=0.2)
Dropout(0.5)
第一个dropout是LSTM层与层之间的dropout,控制输入神经元断开比例。
第二个recurrent_dropout是循环层之间的dropout
第三个Dropout是层与层之间的dropout
TF版本的LSTM有两个dropout,分别控制循环和非循环上的dropout。recurrent_dropout是控制前一时刻隐层状态的断开比例。由于隐层状态不是携带记忆的主体,只是当前节点的上下文表示,所以对其采用dropout,理论上来说不影响长序列的记忆。
一个不太重要的知识点
C t C^t Ct在传递的过程中改变的很慢,而 h t h^t ht在不同的节点往往区别很大。
由于 C t C^t Ct作为主线,主要保存节点传递下来的数据并加入当前节点的内容,改变相对较小。
h t h^t ht主要是利用输出门控信号和当前记忆状态获得,对于不同的输入获得的输出门控信号差别很大,因而不同时刻的 h t h^t ht也会有较大的差别。
LSTM涉及的各种shape详解
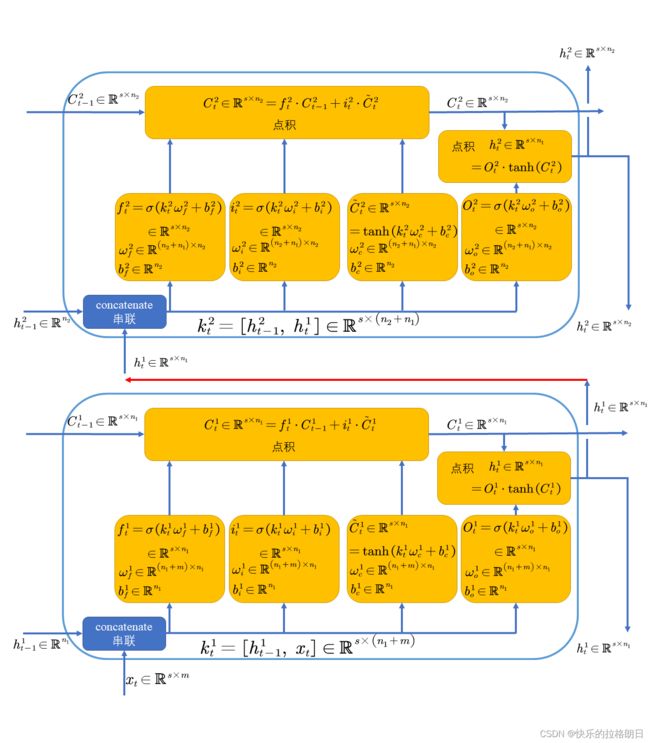
这是一张很经典的图,可以根据此图学习一下LSTM的各种shape。此图画了两个LSTM单元,只看最下面这个单元即可。如果未特别说明,以下符号代表的意义均相同。
- 网络训练时的样本输入shape
这个和LSTM单元输入shape是不一样的,LSTM有单元三个输入,而在网络训练时,我们只需要将样本特征输入即可。
训练时输入数据x的shape: [batch_size, seq_length, dims]
batch_size为批大小,
seq_length为帧数,一般为时间维度,即常说的时间步的数量;
dims为样本提取特征的维数。
在网络计算时,可以理解为每次取出一个sequence进行前向推理,因此在训练时,每个LSTM网络在某个时间步接受[batch_size, dims]的数据,一共循环计算seq_length次。
- LSTM单元的输入
对于LSTM单元来讲共三个输入:隐状态 H t − 1 H_{t-1} Ht−1,单元状态的输入 C t − 1 C_{t-1} Ct−1,还有网络输入的样本特征 X t X_t Xt。其中样本特征和隐状态这两个输入通过串联拼接的方式,变成一个输入。其维度为:[batch_size,seq_length,Hidden_size + dims],其中Hidden_size为隐藏层的输出,也是隐藏层神经元的个数。
- LSTM四组权重的shape:
LSTM神经元内有四组权重,分别为输入门,输出门,遗忘门,生成候选记忆这四组权重。这四组权重其实就是四个全连接层的权重。
每组权重的shape为:[dims + Hidden_size,Hidden_size]
因为LSTM内只有四组权重,因此LSTM参数量总数为:Number_of_weight = 4 * Hidden_size * (Input_size + 1 + Hidden_size),也就是四个全连接层所有权重的数量,也可以写成:4*(Hidden_size*(dims+Hidden_size) + Hidden_size)。最后一个Hidden_size的意义是神经网络的偏置(bias)。
- 隐层状态 H t H_t Ht的shape
所有时刻的隐层状态的shape都是相同的,shape为 [batch_size, Hidden_size]
- 记忆状态 C t C_t Ct的shape
C t C_t Ct的shape:[batch_size, Hidden_size]
- 输出shape,
由下图可以看出LSTM网络有三个输出,分别为output,H,C
output是每个时间步最后一层LSTM的隐状态: o u t p u t = { H 1 , H 2 , . . . , H T } output=\{H_1,H_2,...,H_T\} output={H1,H2,...,HT}。
假设只有一层LSTM的网络,t时刻进行了一次前向推理,获得 H t H_t Ht和 C t C_t Ct,将此刻的 H t H_t Ht加入结果集中。如果有两层LSTM单元,那么就将第二层的隐层输出加到结果集合中去。
由于每一个时刻都会有一个隐藏状态,这样就会有seq_length个隐藏状态,所以输出的维度为[batch_size,seq_length,Hidden_size]
所以输出output是个具有seq_length长度的向量。如果是双向,那么LSTM的output输出维度为 [batch_szie, seq, Hidden_size*num_directions]。
在LSTM层的维度还有两个输出,那就是层的隐状态集合H和记忆状态集合C。有人就问了,前面不是有隐层状态集合output了,怎么又有隐层状态的集合输出?
前面说的隐层状态输出是在时间序列上的输出,而这个隐层状态集合H为层的维度上最后一个时间步的输出。可以参考上图进行理解。每一个LSTM会输出一个隐层状态 H t H_t Ht和记忆状态 C t C_t Ct,如果LSTM单元堆叠了三个,那就有三个隐层状态和三个记忆状态。所以这两个输出为最后一个时间步所有LSTM层的输出。
这两个输出的维度均为: [batch_size,num_layer*num_directions,Hidden_size],num_layer是网络的层数,也就是堆叠了几个LSTM;num_directions表示双向或者单向;
由此可以推导出一个性质,那就是 H [ − 1 ] H[-1] H[−1] == output[: -1 :],即最H的最后一个时间步的最后一层的隐藏层状态与output的最后一个时间步的结果相等。
以上就是LSTM的基本原理与框架,那么在搭建网络时,该用几层LSTM,每个LSTM的权重应该设置多少呢?
Hidden_size大小的选择
隐藏层大小设置,是计算力与表达能力的权衡。越多的hidden_size可以包含更多的细节,以及更丰富的表达能力,但是同时也会带来过拟合以及耗时长等缺点。当神经元足够多时,网络会具有足够多的weights去拟合当前问题,但是换来的可能是过拟合和训练速度严重下降。
从经验来看,很少有人在rnn的层里面加很大的unit数量上去,计算量是很恐怖的,而且获得的效率提高可能只是一点点(比如tensorflow的官方教程里ptb的例子,虽然有1500个hidden unit,但是实际提升相比较于200的并不是很明显)。所以一般128或者256的就已经足够了,单纯RNN的学习能力很一般,需要组合其它手段去提高准确率。
可以想一下,四个全连接层,如果输入维度本身就很大了,再乘以神经元的数量,那这个参数总量是恐怖如斯~
本人曾经将hidden_size设置为很大尝试过,不光训练速度慢,模型的占用空间也是大的惊人…
LSTM堆叠层数的确定
目前查到的资料一般是1、2、3、4层,大部分是一层双向或者两层双向,很少见到更多层数的堆叠。
双向LSTM
了解了LSTM原理,那么双向LSTM自然也不在话下。双向 LSTM 不仅利用了历史信息,也利用了未来信息
其原理是在时间序列上正向和反向调用LSTM。输入在时间维度上反转,得到反向的输出,再将输出按时间维度反转,这样就和正向的输出保持一致。就得到了最终结果。
假设输入为[ x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3]得到输出:[ h 1 , h 2 , h 3 h_1,h_2,h_3 h1,h2,h3]
将输入反转,[ x 3 , x 2 , x 1 x_3,x_2,x_1 x3,x2,x1]得到输出:[ h 1 ′ , h 2 ′ , h 3 ′ h_1',h_2',h_3' h1′,h2′,h3′],将得到的输出反转,得到[ h 3 ′ , h 2 ′ , h 1 ′ h_3',h_2',h_1' h3′,h2′,h1′]
将两个输出进行拼接得到:[ h 1 , h 3 ′ h_1,h_3' h1,h3′],[ h 2 , h 2 ′ h_2,h_2' h2,h2′],[ h 3 , h 1 ′ h_3,h_1' h3,h1′]
情感分类任务,常常使用[ h 1 , h 3 ′ h_1,h_3' h1,h3′],因为其包含前向和反向所有的信息。
TF和pytorch API的差异
- tensorflow的LSTM不支持堆叠。 API:点击这里
TF有三个可以控制输出的参数:return_sequence,return_state,这两个参数均是bool值。
这两个开关对应4中情况:
-
默认情况下,这两个参数都是False。这样就只输出最后一层最后一个时间步的隐藏状态 h n h_n hn,输出维度为[batch_size,Hidden_size*num_directions]
-
return_sequence=True时输出整个序列最后一层的隐藏状态[ h 1 , h 2 , . . . , h n h_1,h_2,...,h_n h1,h2,...,hn],因此输出维度为[batch_size,seq_length,Hidden_size*num_directions]。
-
return_state=True,return_sequence=False时,输出结果有三个:output,h_n,c_n。
output和h_n是相同的,均是最后一个时刻的隐层状态。
c_n则是最后一个时间步的Cell state。他们三个的shape均为[batch_size,Hidden_size*num_directions]
-
当指定return_state=True,sequence=True时,也返回三个值output,h_n,c_n,不过前两个值不再相同,output是所有时间步的隐层状态,h_n,c_n分别为最后一个时间步最后一层的隐层状态和单元状态。其shape参考2,3.
- pytorch的LSTM支持堆叠。 API:点击这里
pytorch结果返回结果有三个:output,(h_n,c_n)。
output:[seq_length,batch_size,Hidden_size*num_directions],pytorch的seq_length和batch_size的位置与TF有所不同
h_n:[num_directions* num_layers,batch_size,Hidden_size],其中输出的维度还可以指定’proj_size‘参数,从而可以从Hidden_size变换成proj_size。
c_n:[num_directions* num_layers,batch_size,Hidden_size]
最后输出的结果
LSTM的缺点
LSTM自有其先天不足,比如:
- RNN计算一个样本,必须一个时间步一个时间步的运行,一个样本的多个时间步无法并行。而CNN和Self-Attention则可以完全并行计算。
- RNN的梯度问题得到了一定的解决,可以处理100个量级的序列,但是对于1000个量级的序列或者更长的序列则依然会很为难;
- 计算费事,由于其内部有4个全连接层,如果LSTM时间步很长,网络节点又多,那么计算量会很大,同时也会很耗时。
参考:
https://arxiv.org/pdf/1409.2329.pdf
https://yongqianxiao.github.io/2020/03/29/LSTM详解及TF手动实现/
https://zhuanlan.zhihu.com/p/42717426
https://zh.d2l.ai/chapter_recurrent-modern/lstm.html
https://www.zhihu.com/question/268394748
https://zhuanlan.zhihu.com/p/139617364