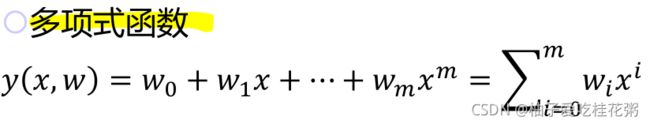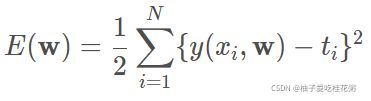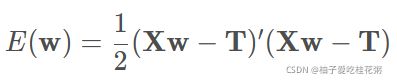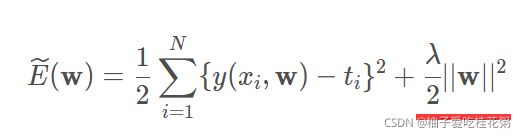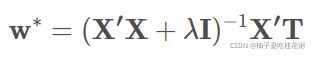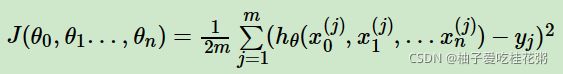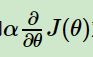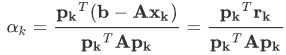机器学习实验1 - 多项式曲线拟合

一、实验要求

1. 生成数据，加入噪声；

2. 用高阶多项式函数拟合曲线；

3. 用解析解求解两种loss的最优解（无正则项和有正则项）

4. 优化方法求解最优解（梯度下降，共轭梯度）；

5. 用你得到的实验数据，解释过拟合。

6. 用不同数据量，不同超参数，不同的多项式阶数，比较实验效果。

7. 语言不限，可以用matlab，python。

求解解析解时可以利用现成的矩阵求逆。梯度下降，共轭梯度要求自己求梯度，迭代优化自己写。不许用现成的平台，例如pytorch，tensorflow的自动微分工具。

二、对实验的理解

首先通过复习搞清楚需要干什么

曲线拟合不难理解，就是通过训练集生成一个拟合函数，从而以后通过给出数据x来预测目标数据t

三、实验步骤

1.生成数据

（为了实现拟合正弦函数，我们要生成数据，并在sinx函数的函数基础上加入噪声）

如何用Python生成数据：（基于matplotlib的python数据可视化）

(7条消息) python 可视化：fig, ax = plt.subplots()画多表图的3中常见样例 & 自定义图表格式_htuhxf的博客-CSDN博客_plt.subplots

(7条消息) 实际应用2： sin(2 * π * x)函数绘制（基于matplotlib的python数据可视化）_简时刻的博客-CSDN博客

(7条消息) 【Python】np.linspace用法介绍_Asher117的博客-CSDN博客

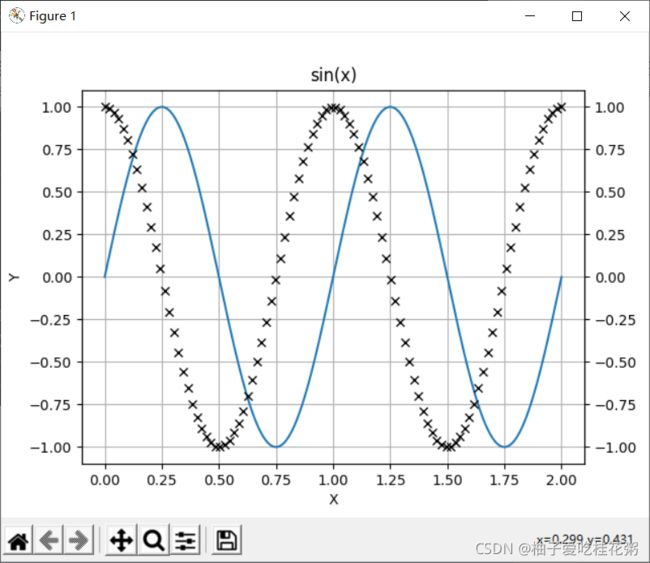
import numpy as np      #导入numpy库，此库用于进行矩阵运算等操作
import matplotlib.pyplot as plt  #导入pyplot绘图库
#例如：  ax = plt.subplots():创建绘图画面    plt.show():显示画面


#x, y为两个向量，对应的x[k],y[k]则是图像上的一个点\
x = np.linspace(0.0,2.0,num=1000) #生成从0.0开始到2.0结束的50个等距向量
y = np.sin(2 * np.pi * x)    # 同样是一个数列，x的sin函数，注意numpy中默认使用弧度制
x2 = np.linspace(0.0,2.0,num = 100)
y2 = np.cos(2 * np.pi * x2)


fig, ax1 = plt.subplots()     # 创建一个绘图界面
ax2 = ax1.twinx()   #让子图2与子图1的x轴一样，这样就可以在一个表中同时表示多个函数了

ax1.plot(x, y)    # 在界面上使用plot方法绘制曲线
ax2.plot(x2,y2,'kx')
#ax.plot(x, y, '--')    # 在界面上使用plot方法绘制短线
#ax.plot(x, y, 'c*')    # 在界面上使用plot方法绘制青色星号
#ax.plot(x, y, 'kx')    # 在界面上使用plot方法绘制黑色叉号
#ax.plot(x, y, 'ro')    # 在界面上使用plot方法绘制红色圆圈
ax1.set(xlabel='X', ylabel='Y',
       title='sin(x)')     # 设置x轴和y轴的标签，曲线的title
ax1.grid()    # 显示网格
plt.show()    # 显示图片

#如果在调试中，只想显示最后一张图，而这张图又和前面的坐标轴不一样（例如记录学习率的图）
#那么，在前面的图中删除plt.show()，添加
plt.close()
#创建最后一张图
plt.plot(x_errorList,errorList)
plt.grid()
plt.show()

效果图：

以上只实现了简单的数据可视化，下面把生成数据封装成函数，这样就可以根据想生成数据的 范围/数据量/基本函数 来得到data了

#函数区
def sin_f(X):
    return np.sin(2 * np.pi * X)

def cos_f(X):
    return np.sin(2 * np.pi * X)
#常量区
X_range = (0.0,2.0)
X_num=100
funcName=sin_f

def getData(X_range, X_num,func):
    X = np.linspace(X_range[0],X_range[1],num=X_num) #生成对应范围和数量的等距向量
    Y = func(X)   #生成X对应函数的值向量
    return X,Y
X, Y = getData(X_range, X_num,funcName)

接下来要在数据中增加噪声，使用np.random.normal()函数添加高斯噪声

(7条消息) np.random.normal()函数_熊大的博客-CSDN博客_np.random.normal

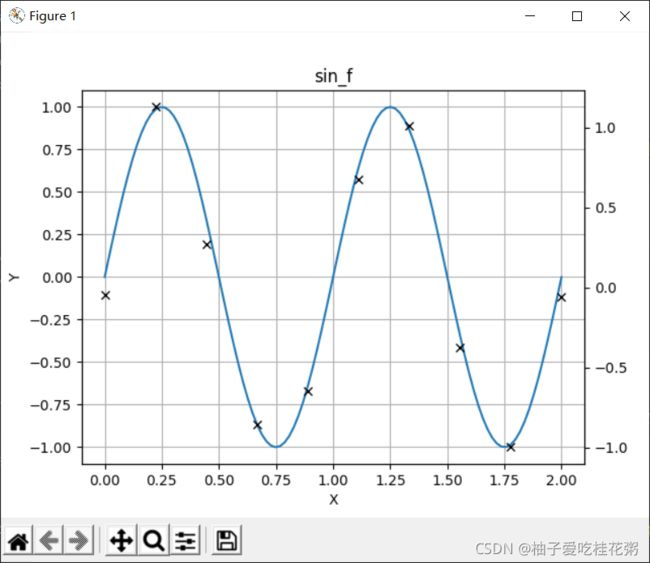
#常量区
X_range = (0.0,2.0)
X_num=100
funcName=sin_f
noise_variance=0.1 #噪声的方差

def getData(X_range, X_num,func,noise_variance):
    X = np.linspace(X_range[0],X_range[1],num=X_num) #生成对应范围和数量的等距向量
    Y = func(X) + np.random.normal(loc=0,scale=noise_variance,size=X_num)   
    #生成X对应函数的值向量,增加了高斯噪声
    return X,Y
X, Y = getData(X_range, X_num,funcName,noise_variance)

最后的效果图：

那么实验要求用以下几种方法来拟合曲线：

2.最小二乘法

① 在加入/不加入惩罚项（正则项）的情况下，用最小二乘法解析解求解两种loss的最优解

1）不加入惩罚项：

我们往往采用多项式来拟合函数

y(x,w)是我们假设的多项式拟合函数，x是每个我们已知的样本数据，w是参数，m是阶数

我们的目的是得到使E(x)最小的参数w

  

拟合好坏的判断标准 ：（就是计算预测函数和真实函数的误差）

用最小二乘法建立误差函数E(w)来测量

 关于最小二乘法：（虽然但是很简单刚开始看到这个名词是真有点懵）

最小二乘法（least sqaure method） - 知乎 (zhihu.com)

观测值就是我们的多组样本，理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使目标函数最小化时候的假设拟合函数

例子： 

比如我们有 m 个只有一个特征的样本

每个样本点目标值 t （即样本的y）与预测函数y(x,w)之间的误差

其中式子之前的1/2仅仅是为了后续求导方便，无实际意义

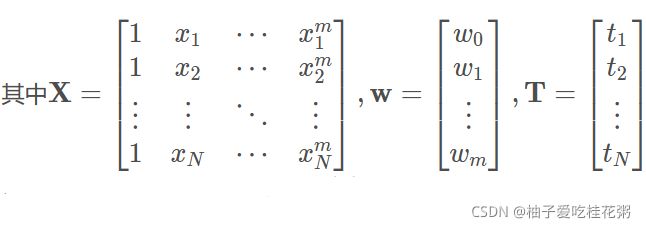
 那么对于计算机处理的数据量，我们把他变为矩阵形式：

 

 

(7条消息) np.column_stack用法_Rock的博客-CSDN博客_np.column_stack

如何在python中将列向量拼接为矩阵形式：

numpy的矩阵拼接函数：

 X = np.column_stack((X,pow(x,i)))

将2个矩阵按列合并，注意这些矩阵都要在括号中（否则报错）

效果：

M = 4  #阶数

def get_matrix(x, M):
    X = pow(x,0)
    for i in range (1,M+1):
        X = np.column_stack((X,pow(x,i)))
    return X

X = get_matrix(x, M)
print(X)
T = y   #目标值t

  

 可知，E(w)是关于w的二次函数，想要得到使误差函数E(x)最小的参数w，求导并令∂E/∂w=0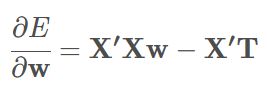

 得到唯一的w*解

 

接下来编写函数用此公式得w

用到的np矩阵计算参数W：

NumPy 线性代数 | 菜鸟教程 (runoob.com)

np.linalg.inv(Matrix):  numpy中求矩阵的逆

numpy.dot(a, b, out=None): 两个数组的点积，即元素对应相乘,可选结果保存在out中

a.T ：对a进行转置

def noPunishment_LeastSquareM(X, T):
    W = np.linalg.inv((X.T).dot(X)).dot(X.T).dot(T) #公式W* = (X'·X)-1 (X')·T
    return W 


W = noPunishment_LeastSquareM(X, T) #W的计算使用样本的X
Y = X2.dot(W)   #画出预测函数的值，X2·W得到的是一个样本数*1的向量

这样就可以算出W，就可以得到预测函数了，其Y值用较多的 X2 · W

那么用我们得到的W，就可以画出

plt.plot(x2, y2,'-b',x,y,'kx',x2,Y,'-r')    # 在界面上使用plot方法绘制曲线 
    #x2y2为二次函数曲线，xy为叉号表示的样本点，x2Y为得到的拟合函数

  

记录每次M的误差函数并绘图：

#--------------------------------------------------------------------------------------->计算误差函数ERMS
def get_ERMS(Sample_num):
    ERMS = ((X.dot(W)-T).T.dot((X.dot(W))-T))/(2*Sample_num)
    return ERMS

errorList=list()    #记录不同阶数的错误率List
errorList.append(get_ERMS(Sample_num))  #计算这次循环的错误率，并加入到 errorList向量中

#绘制不同M下的学习率
x_errorList = np.linspace(1,Sample_num,Sample_num-1)
plt.plot(x_errorList,errorList)
plt.grid()
plt.show()

 

2）加入惩罚项：

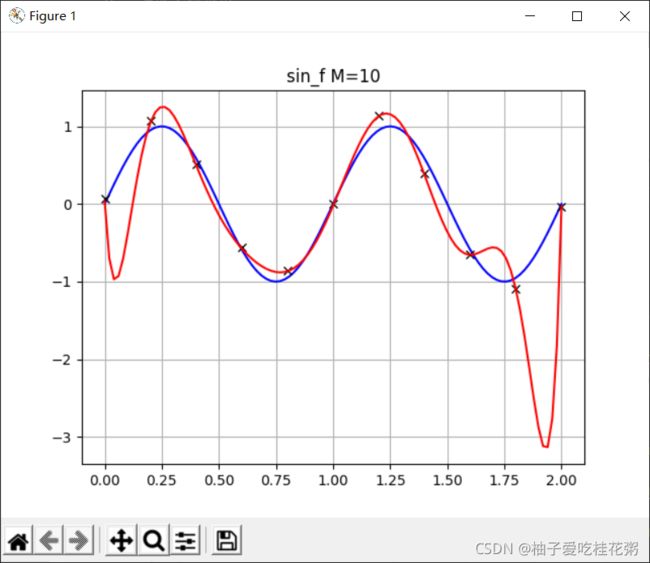
 在不加入惩罚项时，我们可以观察到在M较大的时候，出现了过拟合现象

（过拟合现象也可以增大样本数量来解决，但样本数量有限的情况下考虑增加正则项）

此时误差很小，但曲线失去了正弦形状，原因是阶数越大时，最佳拟合曲线的参数w*绝对值（范数）越大。为了避免这种情况，我们在E(w)中增加对w的惩罚项（正则项）

  将其写为矩阵形式：

 求导，得w*

#------------------------------------------------------------------------------------->带惩罚项最小二乘法拟合
def hasPenalty_LeastSquareM(X, T,penalty_lambda,M):
    W = np.linalg.inv((X.T).dot(X) + np.identity(M+1)*penalty_lambda).dot(X.T).dot(T)   #公式：W* = (X'·X+λI)-1·(X'·T)
    return W 

 如何选取正则项中的λ：

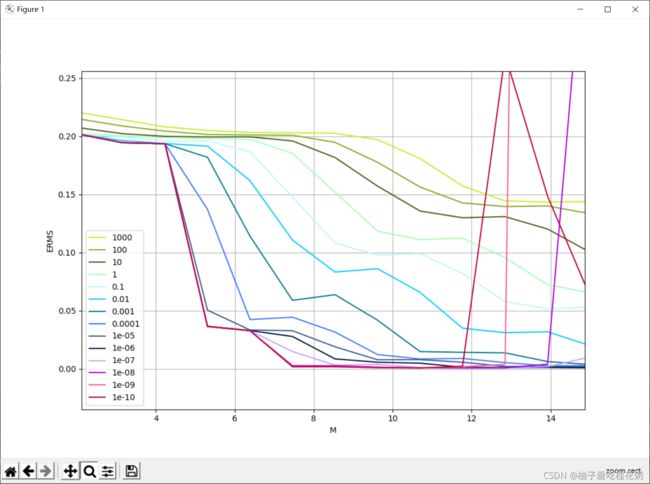
我们也是通过计算ERMS来确定，对于不同训练集，超参数λ的选择不同

观察不同λ取值的ERMS,可以看到，

当λ较大时（1000-1e-3,不会出现错误率剧烈上升的情况，但错误率并不低

当λ较小时(1e-4-1e-10),错误率较低，但样本数过大时，错误率会变得非常大

对于样本量在15的情况，选择 λ = 1e-6 较为合适

3.梯度下降法

梯度下降（Gradient Descent）小结 - 刘建平Pinard - 博客园 (cnblogs.com)

1）原理：

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)',简称grad f(x,y)或者▽f(x,y)

在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数。

 2）算法步骤：

①确认优化模型的假设函数和损失函数：

假设函数：(增加特征x0=1) 

其中， 假设函数hθ(X)为sample_num*1的向量,θ为(m+1)*1的向量，X为sample_num*(m+1)维的矩阵。sample_num代表样本的个数，m+1代表样本的特征数

 定义损失函数loss：

其中，Y是样本的输出值，维度为sample_num*1

 ② 算法相关参数初始化：

初始化θ0,θ1...,θn,算法终止距离ε以及步长α

在没有任何先验知识时，先所有的θ初始化为0， 将步长α初始化为1。后续再调优

③ 确定当前位置的损失函数的梯度，对于θi,其梯度表达式如下：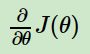

 ④用步长乘以损失函数的梯度，得到当前位置下降的距离，即

 ⑤确定是否所有的θi梯度下降的距离都小于ε，如果小于ε则算法终止，当前所有的θi(i=0,1,...n)即为最终结果，否则进入步骤⑥

⑥更新所有的θ，对于θi，其更新表达式如下（减去下降的距离） 

   

        更新完毕后继续转入步骤③.

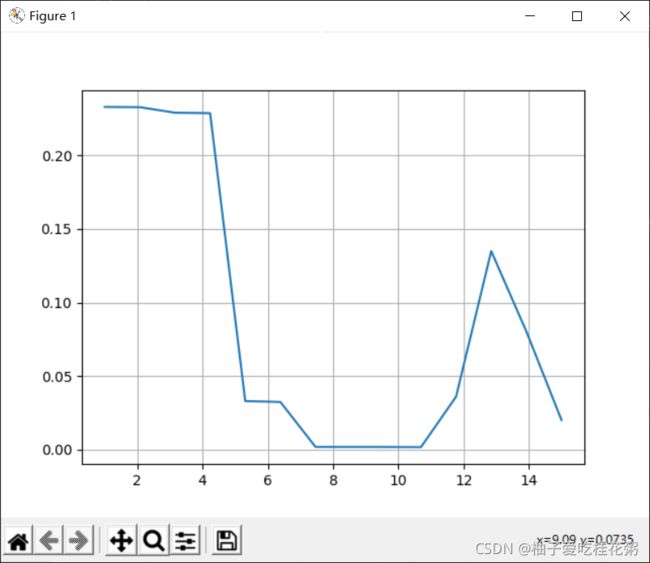
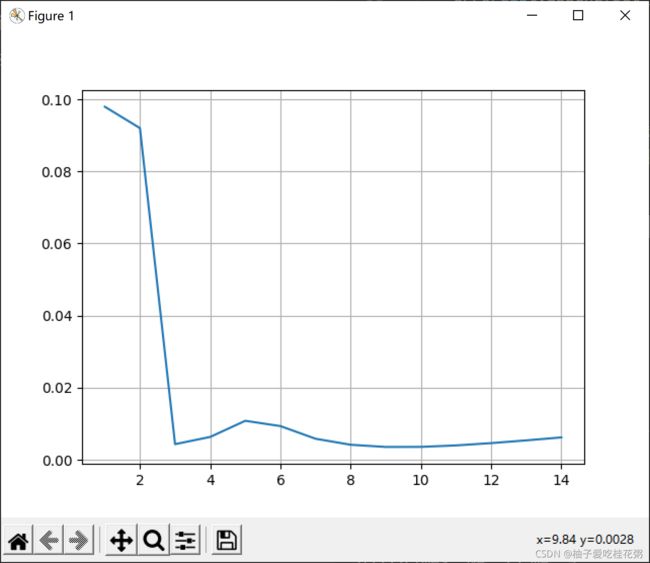
学习率：可以看出在11时错误率最低，且几乎没有过拟合现象

③用共轭梯度法拟合曲线

理解共轭梯度法：

(8条消息) （一）共轭梯度算法_秦时明月的博客-CSDN博客_共轭梯度法

梯度下降法是沿着梯度的负方向最小化目标函数；梯度下降在寻找搜索方向的时候只利用了空间中当前点的信息

共轭方向法是把x表示成相对于系数矩阵A共轭的一组基向量的线性组合，然后每次沿着共轭方向一维最小化目标函数。共轭梯度下降还利用了之前的搜索路径信息

        相比于梯度下降法，共轭梯度法用占比高的向量组和进行逼近，而不需要把所有的向量都组合在一起，通过仔细挑选共轭向量P来重建方程的解。在解形如Ax=b的方程组时，他要求A必须是正定的。

作为一种典型的共轭方法，其每一次搜索的方向都是共轭的，而这些搜索方向d仅仅是负梯度方向与上一次迭代的搜索方向的组合，因此，存储量少，计算方便。

对于第k步的残差rk=b-Axk，我们根据 残差去构造下一步的搜索方向pk，初始时我们令p0=r0。然后利用Gram-Schmidt方法一次构造互相共轭的搜索方向pk，具体构造时需要先求得第k+1步的残差，即rk+1=rk-αkApk，其中αk为

根据第k+1步的残差构造下一步的搜索方向pk+1=rk+1+βk+1pk，其中βk+1=rk+1Trk+1/rkTrk。然后可以得到xk+1=xk+αkpk 。另由于学习率的计算中涉及计算pkTApk，因此我们需要将X矩阵转换成方阵，即进行转化在Ax=b左右两边同时乘以xT，因为是同解的，所以对转换后的矩阵进行求解即可。

为了缓解过拟合现象，只需要在同解变换时加入一项超参数乘单位阵作为惩罚项即可。

 

④解释过拟合

⑤改变样本数量、超参数、阶数 比较实验结果