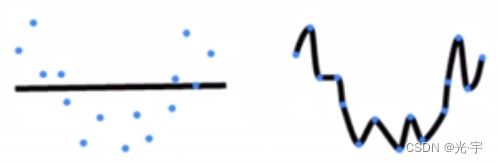pytorch深度学习实战lesson12

第十二课 模型选择与过/欠拟合

目录

理论部分

    模型选择

    过拟合和欠拟合

实践部分

---

理论部分

模型选择

首先介绍一下如何选择超参数

从一个简单的例子开始：

《预测谁会偿还贷款》

背景：

然后你惊讶的发现：

（在美国，穿蓝色衬衫有个隐藏信息——蓝领）

这里的问题就是：面试本来穿的蓝色衣服，结果下次见面穿了红色衣服，这两种模型就不一样了，也就是说，模型会认为一个人前后穿了两种颜色的衣服后，它会认为这也是两个人。这个肯定就不对了。

所以要对这个问题进行研究。

看这个问题的方法通常来讲是通过看误差。

这里主要关注泛化误差。

计算训练误差和泛化误差的主要途径是通过验证数据集和测试数据集：

当没有足够多的数据时，也就是说训练集的数据比较少的话但测试集的数据集多就会有点亏。此时要用这个方法：

如下图所示会拿到三个验证的精度“val”，对其求平均即可。

过拟合和欠拟合

这个表格表明：对于简单的数据集，使用低层次的模型才会得到正确的结果，不然就过拟合；对于复杂的数据集，才适合使用高层次的模型。

模型的容量是指弥合各种函数的能力：低容量的模型难以拟合训练数据；高容量的模型可以记住所有的训练数据。

下图所示，左边是欠拟合，右边是过拟合。

模型容量的影响：

这里我们主要达成的目的是：1、将蓝点尽量往下拉；2、让红圈中的区域尽量小。

有时我要把最优处的泛化误差往下拉时，不得不承受一定程度的过拟合，其实过拟合并不是个坏概念，首先模型容量要充足，这样才有了控制容量的资本，这样才能使泛化误差往下降。

所以我们接下来可以估计一波模型容量。

（此图第三行应为“树模型”）

模型容量估计方法一：如上图所示，可以通过线性模型和单层感知机模型参数的个数进行容量的估计。

模型容量估计方法二：假设模型的参数只能在一个小范围里面取值的话，就可以认为这个模型的容量是比较低的；反之，如果模型的参数能在一个大范围里面取值的话，就可以认为这个模型的容量是比较高的。

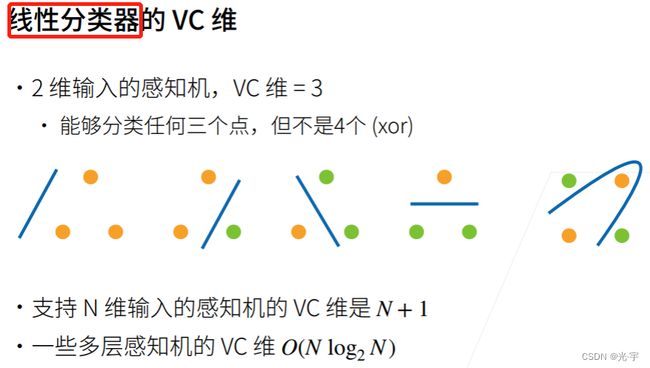
对一个分类模型来讲，有一个著名的理论：VC维。（不是维生素！不是维生素！不是维生素！达咩！达咩！达咩！）

注意这里是线性分类器，所以，我要得出的分类模型是一根直线，而不能是曲线。所以对于2维输入的感知机，我如果想用线性分类器进行分类的话，这个2维输入必须只有三个以内的点才行，如上图所示。如果4个点的话，比如xor函数的话得出的分类模型就是根曲线了，就不是线性分类器了。

总结：

模型容量需要匹配数据复杂度，否则可能导致欠拟合和过拟合；

统计机器学习提供数学工具来衡量模型复杂度；

实际中一般靠观察训练误差和验证误差。

实践部分

代码：

#通过多项式拟合来交互地探索这些概念
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
#使用以下三阶多项式来生成训练和测试数据的标签：
max_degree = 20
n_train, n_test = 100, 100
true_w = np.zeros(max_degree)
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])

features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
    poly_features[:, i] /= math.gamma(i + 1)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)
#看一下前2个样本
true_w, features, poly_features, labels = [
    torch.tensor(x, dtype=torch.float32)
    for x in [true_w, features, poly_features, labels]]
print(features[:2], poly_features[:2, :], labels[:2])
#实现一个函数来评估模型在给定数据集上的损失
def evaluate_loss(net, data_iter, loss):
    """评估给定数据集上模型的损失。"""
    metric = d2l.Accumulator(2)
    for X, y in data_iter:
        out = net(X)
        y = y.reshape(out.shape)
        l = loss(out, y)
        metric.add(l.sum(), l.numel())
    return metric[0] / metric[1]
#定义训练函数
def train(train_features, test_features, train_labels, test_labels,
          num_epochs=400):
    loss = nn.MSELoss()
    input_shape = train_features.shape[-1]
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
    batch_size = min(10, train_labels.shape[0])
    train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),
                                batch_size)
    test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),
                               batch_size, is_train=False)
    trainer = torch.optim.SGD(net.parameters(), lr=0.01)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
                            xlim=[1, num_epochs], ylim=[1e-3, 1e2],
                            legend=['train', 'test'])
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(
                net, train_iter, loss), evaluate_loss(net, test_iter, loss)))
    print('weight:', net[0].weight.data.numpy())
#三阶多项式函数拟合(正态)把样本的前四列进行训练
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
      labels[:n_train], labels[n_train:])
plt.show()
#线性函数拟合(欠拟合)把样本的前2列进行训练
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
      labels[:n_train], labels[n_train:])
plt.show()
#高阶多项式函数拟合(过拟合)把所有样本进行训练
train(poly_features[:n_train, :], poly_features[n_train:, :],
      labels[:n_train], labels[n_train:], num_epochs=1500)
plt.show()

tensor([[0.5105],
        [1.7914]]) tensor([[1.0000e+00, 5.1052e-01, 1.3032e-01, 2.2176e-02, 2.8304e-03, 2.8900e-04,
         2.4590e-05, 1.7934e-06, 1.1444e-07, 6.4918e-09, 3.3142e-10, 1.5382e-11,
         6.5439e-13, 2.5698e-14, 9.3711e-16, 3.1894e-17, 1.0177e-18, 3.0562e-20,
         8.6680e-22, 2.3290e-23],
        [1.0000e+00, 1.7914e+00, 1.6045e+00, 9.5809e-01, 4.2907e-01, 1.5373e-01,
         4.5897e-02, 1.1746e-02, 2.6301e-03, 5.2349e-04, 9.3777e-05, 1.5272e-05,
         2.2798e-06, 3.1415e-07, 4.0197e-08, 4.8005e-09, 5.3747e-10, 5.6636e-11,
         5.6365e-12, 5.3142e-13]]) tensor([5.2693, 7.0454])

weight: [[ 5.004308   1.206558  -3.3976068  5.571822 ]]

weight: [[3.3495877 3.4845173]]

weight: [[ 5.0008197   1.2990634  -3.3748832   5.074504   -0.09170274  1.3520207
   0.42564648  0.22717157  0.18736452  0.17358267  0.19561997 -0.01042124
   0.03830591  0.0619094  -0.2167484  -0.11080281  0.07579094 -0.06983274
  -0.12986308  0.1677877 ]]