python数据挖掘学习笔记——岭回归和lasso回归

众所周知，当数据具有较强的多重共线性的时候便无法使用普通的多元线性回归，这在数学上有严谨的证明但本文并不做介绍。有关公式的推导本文均不做说明，如有需要可在论文写作时查阅参考文献。 本文仅供个人学习时记录笔记使用
Reference：《从零开始学Python数据分析与挖掘》

岭回归

可视化方法确定λ的值

岭回归的系数是关于λ的函数，可通过对回归系数的折线图确定合理的λ的数值，一般而言回归系数随着λ值的增加而趋近于稳定的点就是需要的λ的数值。
使用的模块：sklearn子模块linear_model中的Ridge类

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn.linear_model import Ridge, RidgeCV

diabetes = pd.read_excel(r'diabetes.xlsx')  # 读取数据集d
# 构造自变量，剔除患者性别，年龄和因变量
predictors = diabetes.columns[2 : -1]
X_train, X_test, y_train, y_test = model_selection.train_test_split(diabetes[predictors], diabetes['Y'], test_size = 0.2, random_state = 1234)

# 构造不同的lambda数值，范围从lg10e-5 到 lg10e+2
Lambdas = np.logspace(-5, 2, 200)	
# 构造空列表用于存储模型的回归系数
ridge_cofficients = []
# 循环迭代不同的lambda值
for Lambda in Lambdas:
    ridge = Ridge(alpha=Lambda, normalize=True)
    ridge.fit(X_train, y_train)	# 计算β的数值
    ridge_cofficients.append(ridge.coef_)	# 将β存入结果，6个自变量的系数。
    
    
# 绘制alpha的对数与回归系数的关系
# 中文乱码和坐标轴负号的处理
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘图风格
plt.style.use('ggplot')
plt.plot(Lambdas, ridge_cofficients)
# 对x轴做对数处理
plt.xscale('log')
# 设置折线图x轴和y轴坐标
plt.xlabel('Log(Lambda)')
plt.ylabel('Cofficients')

通过Ridge类完成岭回归模型的求解的参数设置，基于fit方法实现模型偏回归系数的求解。

·图象说明：每条折线代表了不同的遍历，对于比较突出的喇叭形折线，一般代表变量存在多重共线性。λ越趋近于0，β越与线性回归模型的最小二乘解完全一致。最后λ在0.01附近时绝大多数变量的回归系数趋于稳定，故lambda的数值可以选择0.01附近。
·代码解释：代码块中的注释。

交叉验证法确定λ值

图形法只能大致地看出λ的取值，但要具体的求出λ的数值可以通过交叉验证的方法求解。对于交叉验证的思想如下图所示(图源西瓜书)：将数据集分成若干份，取其中的一份作为验证集，其余的作为训练集，并让每个数据集都有一次当验证集的机会，以此类推全部训练结束后得到返回结果。python中可以使用sklearn子模块linear_model中的RidgeCV类来实现k重交叉验证。

ridge_cv = RidgeCV(alphas = Lambdas, normalize=True,
                   scoring='neg_mean_squared_error', cv = 10)
ridge_cv.fit(X_train, y_train)
ridge_best_Lambda = ridge_cv.alpha_
print('最佳的λ的值为：', ridge_best_Lambda)

输出结果：最佳的λ的值为： 0.014649713983072863

代码解释：通过ridge_cv()函数进行10折交叉验证。
·alphas = lambdas，用于指定多个lambda值的元组或数组对象
·normalize：表示是否对数据进行标准化，默认为False
·scoring：评估模型的度量方法
·cv：指的是交叉验证的重数
·gcv_mode：用于指定执行广义交叉验证的方法

模型的预测

# 基于最佳的lambda进行建模
ridge = Ridge(alpha=ridge_best_Lambda, normalize=True)
ridge.fit(X_train, y_train)
res = pd.Series(index=['Intercept'] + X_train.columns.tolist(),
          data = ['ridge.intercept_'] + ridge.coef_.tolist())

print('最终求解的模型的参数为：\n', res)

from sklearn.metrics import mean_squared_error

# 模型的预测
ridge_predict = ridge.predict(X_test)
# 预测结果验证
RMSE = np.sqrt(mean_squared_error(y_test, ridge_predict))
print('预测结果 :', ridge_predict)
print('验证结果RMSE = ', RMSE)

代码解释：
首先先是利用前文所求出的最佳的λ数值进行建模，利用Ridge()函数进行建模，alpha的数值此时选用最佳的λ。最终求解出方程的系数，其解释与OLS线性回归方程相似。

lasso回归

相对于岭回归，lasso回归与其的区别主要体现在惩罚项的不同，前者是β的平方项，而后者是β的绝对值（详细可查阅文献资料）虽然二者的存在都是为了解决线性回归模型中的共线性等问题，但目前lasso回归的使用会更多。同样的，数学理论推导本文不做描述，只介绍python的应用。

可视化处理

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn.linear_model import Lasso, LassoCV

diabetes = pd.read_excel(r'diabetes.xlsx')  # 读取数据集d
# 构造自变量，剔除患者性别，年龄和因变量
predictors = diabetes.columns[2 : -1]
X_train, X_test, y_train, y_test = model_selection.train_test_split(diabetes[predictors], diabetes['Y'], test_size = 0.2, random_state = 1234)
Lambdas = np.logspace(-5, 2, 200)

lasso_cofficients = []
for Lambda in Lambdas:
    lasso = Lasso(alpha=Lambda, normalize=True, max_iter=10000)
    lasso.fit(X_train, y_train)
    lasso_cofficients.append(lasso.coef_)
    
# 绘制Lambda与回归系数的这线图
plt.plot(Lambdas, lasso_cofficients)
plt.xscale('log')
plt.xlabel('Lambda')
plt.ylabel('Cofficients')

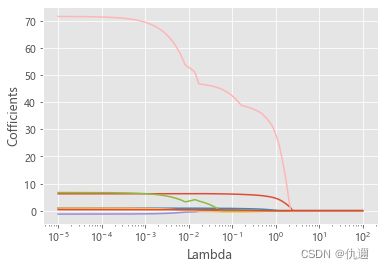
代码解释：数据上，仍然使用前文的数据集，测试集、验证集的划分，λ的选取都仍染沿用前文。lasso回归的λ求解函数Lasso()与岭回归的Ridge()的用法类似，其中的参数便不再赘述，不同之处在于，max_iter这里规定了最大迭代次数。
对于结果，与前文的解释类似，折现趋近于0的时候的λ值最优，且喇叭形曲线表明该变量的多重共线性越强。

交叉验证法确定λ

可视化处理仅仅只能作为初步的确定，需要得到精确结果还是需要进行交叉验证法来确定λ的数值。同样的，这里我们使用的是sklearn模板中的子模版linear_model中的lasso_CV类来进行求解。

# 交叉验证
lasso_cv = LassoCV(alphas=Lambdas, normalize=True, cv = 10, max_iter = 10000)
lasso_cv.fit(X_train, y_train)

# 输出最佳的lambda数值
lasso_best_alpha = lasso_cv.alpha_
print(lasso_best_alpha)

这里的参数含义与Ridge类似，便不再赘述。

模型的预测

# 模型的预测
# 系数输出
lasso = Lasso(alpha=lasso_best_alpha, normalize=True, max_iter=10000)
lasso_model = lasso.fit(X_train, y_train)

res = pd.Series(index = ['Intercept'] + X_train.columns.tolist(),
                data = [lasso.intercept_] + lasso.coef_.tolist())
print(res)

# 预测
lasso_predict = lasso.predict(X_test)
RMSE = np.sqrt(mean_squared_error(y_test, lasso_predict))

根据前文，通过10折交叉验证得到的最优的lambda数值将用于最终的模型建立。EMSE作为均方误差作为模型评估的标准，同样的，lasso参数设置与Ridge类似，不做赘述。
根据上述模型，对同一个数据集分别通过岭回归和lasso回归建模后，得到的RMSE后者比前者小了0.8左右，这表明在降低模型的复杂度的情况下，模型的拟合效果得到了进一步的提高。绝大多数情况下，lasso回归得到的系数比岭回归的系数更加可靠且易于解释。