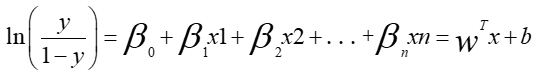【学习笔记】二元Logistic回归预测
目录
- 1.基本含义和思想
- 2.论文[3]进行回归预测的思路是什么?
- 3.求逻辑回归模型的数学过程
-
- 3.1 改写函数
- 3.2 函数变换
- 3.3 得到离散概率
- 3.4 最大似然法
- 3.5 牛顿法
- 4.逻辑回归在论文[3]中的应用
- 参考文章
- 参考文献
1.基本含义和思想
Logistic回归和线性回归最大的区别在于,Y的数据类型。线性回归分析的因变量Y属于定量数据,而Logistic回归分析的因变量Y属于分类数据。分类数据指的是,Y的结果不是一个值(量),而是一个类别,比如一件衣服的是否有人想购买?这里的Y是“是否愿意购买”,属于分类数据。如果Y值仅两个选项,分别是有和无之类的分类数据,选择二元Logistic回归分析。
因此,逻辑回归(Logistic regression)是一种基于因变量为二项分布的广义线性模型,当需要通过一系列连续型或类别型预测变量来预测二值型结果时是一个非常有用的工具。
逻辑回归之所以能轻松解决分类问题,仅仅是在一般线性回归模型的基础上采用了Logistic 函数。Logistic 函数又称为 Sigmoid 函数,函数形式为:

因此,使用 Logistic 函数将自变量映射到(0,1)上。
2.论文[3]进行回归预测的思路是什么?
已知某个特定用户在某两个相邻的支付时刻之间,所有的点击、收藏和加购物车的累计次数,作为解释变量(可以理解为自变量),是否有支付行为作为被解释变量(可以理解为因变量),我们要做的就是根据已知数据建立模型p= y (x1,x2,…,xn),p是支付的概率,建立模型的过程就是求解Logistic函数中参数的过程,最终通过迭代得到完整的Logistic函数,便能够根据该模型,通过下一阶段用户的点击、收藏和加购物车的次数预测该用户进行支付动作的概率。
因此最重要的就是如何建立该模型,也就是Logistic函数,即求参数,下面开始详细讨论。
3.求逻辑回归模型的数学过程
3.1 改写函数
首先,改写z,令其等于自变量的线性组合的形式,如下:

令wT=(β1, β2, …, βn),x=(x1,x2,…,xn)T,b=β0,进行步骤3.2
3.2 函数变换
下面对Sigmoid函数进行变换,参考周志华所著《机器学习》:

周志华在书中提到:由此可看出,式(3.18)实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率,因此,其对应的模型称为"对数几率回归" (logistic regression,亦称logit regression)。
3.3 得到离散概率
继续参考《机器学习》的步骤:

(3.23)其实就等价于(3.17)的形式,简单变换了一下。
记βT=(wT;b)=(β1, β2, …, βn, b);
x┴∧ =(x;1)T=(x1,x2,…,xn,1)T
记(3.23)为p1,(3.24)为p0
将两式合并得到:
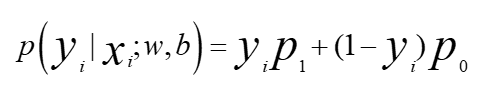
求对数,并整理得到(*)式:
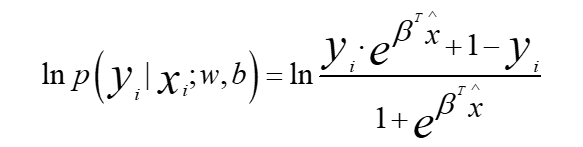
3.4 最大似然法
因此,开始运用最大似然估计法求取未知量β,其思想是使得观测数据(样本)发生概率最大的参数就是最好的参数。
给定数据集:
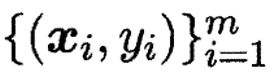
那么似然函数就应该是这些观测值均发生的概率的乘积,使其最大。但为了求解方便,我们通常会将似然函数转成对数似然函数,然后再求解(可以转成对数似然函数的主要原因是对数函数并不影响函数的凹凸性)。写出似然函数如下:
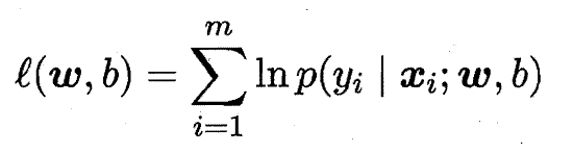
将步骤3.3的(*)式代入并取相反数得()式:
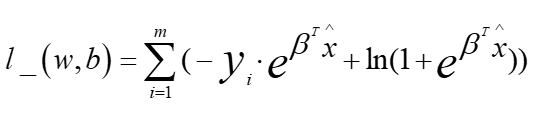
问题转化为求()式的最小值。
3.5 牛顿法
接着利用经典的数值优化算法如梯度下降法(gradient descent method) 、牛顿法(Newton method)等都可求得其最优解。
牛顿法的思想:基本牛顿法是一种是用导数的算法,它每一步的迭代方向都是沿着当前点函数值下降的方向。即通过求解目标函数一阶导为零的参数值,进而求得目标函数最小值。
梯度下降法的思想:梯度是函数在某点处的一个方向,并且沿着该方向变化最快,变化率最大。因此梯度下降的方向就是在该点处使值变小最快的方向。
参照《机器学习》有:

至此,可以求出模型中的β,也就是所有的参数了。
4.逻辑回归在论文[3]中的应用
对于论文[3]提到的数据集,其中x1, x2, x3即为cl(click点击),fa(favorite收藏),ca(cart加入购物车)在两个支付行为之间的累计操作次数,pa为是否支付(1为支付,0为未支付)因此有如下公式:
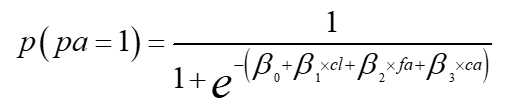
利用上述方法进行编程计算就可以求出所有的未知参数,得到回归模型,从而对于输入x=(cl,fa,ca),可以得到输出p(pa=1),即支付的概率,达到预测的目的。
参考文章
Logistic回归(Logistic Regression):
https://www.jianshu.com/p/5631698e8379
二元逻辑回归实现鸢尾花数据分类(python):
https://www.jianshu.com/p/ca1e295813b8
最小二乘法原理(后):梯度下降求权重参数:
https://mp.weixin.qq.com/s?__biz=MzI3NTkyMjA4NA==&mid=2247484070&idx=1&sn=98e6d2386d3d4d2db2afc35ef163b406&chksm=eb7c2f6ddc0ba67b925f435c391278e21ce56c073551e1939805e30570e1ade263e7395fda6f&scene=21#wechat_redirect
深度学习—— 最小二乘法 & 极大似然估计 & 梯度下降法:
https://blog.csdn.net/qq_34872215/article/details/88302532
参考文献
[3]唐慧祥,常啸,宋来敏.基于数据挖掘的淘宝精准营销策略研究[J].哈尔滨师范大学自然科学学报,2020,36(03):19-24.
[17]马姝.基于数据挖掘的消费者购买预测的研究[D].云南财经大学,2016.
[18]周志华. 机器学习 : = Machine learning[M]. 清华大学出版社, 2016.