NNDL 作业8:RNN - 简单循环网络
简单循环网络( Simple Recurrent Network , SRN)只有一个隐藏层的神经网络 .
目录
-
- 1. 使用Numpy实现SRN
- 2. 在1的基础上,增加激活函数tanh
- 3. 分别使用nn.RNNCell、nn.RNN实现SRN
- 4. 分析“二进制加法” 源代码(选做)
- 5. 实现“Character-Level Language Models”源代码(必做)
- 6. 分析“序列到序列”源代码(选做)
- 7. “编码器-解码器”的简单实现(必做)
- 总结
- 参考
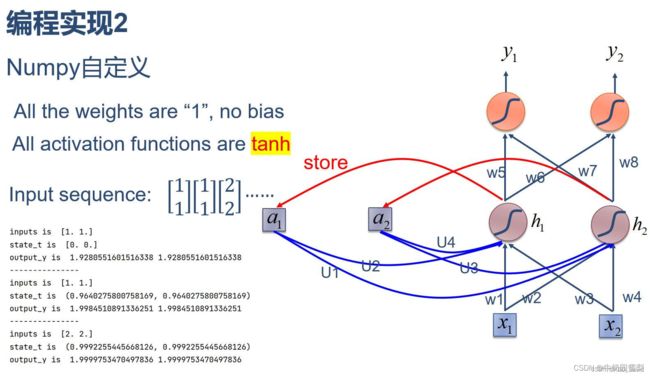
1. 使用Numpy实现SRN
# coding=gbk
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t)
in_h2 = np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t)
state_t = in_h1, in_h2
print('a',state_t,in_h1,in_h2)
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
运行结果:
inputs is [[1. 1.]
[1. 1.]
[2. 2.]]
state_t is [0. 0.]
--------------------------------------
inputs is [1. 1.]
state_t is [0. 0.]
a (2.0, 2.0) 2.0 2.0
output_y is 4.0 4.0
---------------
inputs is [1. 1.]
state_t is (2.0, 2.0)
a (6.0, 6.0) 6.0 6.0
output_y is 12.0 12.0
---------------
inputs is [2. 2.]
state_t is (6.0, 6.0)
a (16.0, 16.0) 16.0 16.0
output_y is 32.0 32.0
---------------
2. 在1的基础上,增加激活函数tanh
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.tanh(np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t))
in_h2 = np.tanh(np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t))
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
运行结果:
inputs is [[1. 1.]
[1. 1.]
[2. 2.]]
state_t is [0. 0.]
--------------------------------------
inputs is [1. 1.]
state_t is [0. 0.]
output_y is 1.9280551601516338 1.9280551601516338
---------------
inputs is [1. 1.]
state_t is (0.9640275800758169, 0.9640275800758169)
output_y is 1.9984510891336251 1.9984510891336251
---------------
inputs is [2. 2.]
state_t is (0.9992255445668126, 0.9992255445668126)
output_y is 1.9999753470497836 1.9999753470497836
---------------
3. 分别使用nn.RNNCell、nn.RNN实现SRN

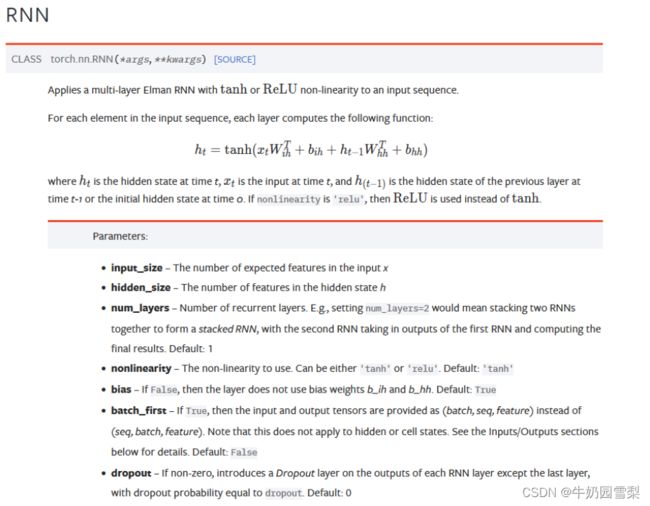
nn.RNN
使用nn.RNN方法有三个参数(input_size,hidden_size,num_layers)
input_size是word_embedding的维度,比如用100维的向量来表示一个单词,那么input_size就是100;如果预测的是房价,房价就一个数字,那么input_size就是1
hidden_size是指memory size,我们用一个多长的向量来表达
h是最后一个时间戳上面的所有memory的状态
out是所有时间戳上面最后一个memory的状态
nn.RNNCell
相比一步到位的nn.RNN,也可以使用nn.RNNCell,它将序列上的每个时刻分开来处理。
也就是说,如果要处理的是3个句子,每个句子10个单词,每个单词用长100的向量,那么送入nn.RNN的Tensor的shape就是[10,3,100]。
但如果使用nn.RNNCell,则将每个时刻分开处理,送入的Tensor的shape是[3,100],但要将此计算单元运行10次。显然这种方式比较麻烦,但使用起来也更灵活。

1、用torch.nn.RNNCell()
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.tanh(np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t))
in_h2 = np.tanh(np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t))
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
运行结果:
inputs is [[1. 1.]
[1. 1.]
[2. 2.]]
state_t is [0. 0.]
--------------------------------------
inputs is [1. 1.]
state_t is [0. 0.]
output_y is 1.9280551601516338 1.9280551601516338
---------------
inputs is [1. 1.]
state_t is (0.9640275800758169, 0.9640275800758169)
output_y is 1.9984510891336251 1.9984510891336251
---------------
inputs is [2. 2.]
state_t is (0.9992255445668126, 0.9992255445668126)
output_y is 1.9999753470497836 1.9999753470497836
---------------
2、torch.nn.RNN
import torch
batch_size = 1
seq_len = 3
input_size = 2
hidden_size = 2
num_layers = 1
output_size = 2
cell = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers,nonlinearity='relu')
for name, param in cell.named_parameters(): # 初始化参数
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
inputs = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(num_layers, batch_size, hidden_size)
out, hidden = cell(inputs, hidden)
print('out',out,hidden)
print('Input :', inputs[0])
print('hidden:', 0, 0)
print('Output:', liner(out[0]))
print('--------------------------------------')
print('Input :', inputs[1])
print('hidden:', out[0])
print('Output:', liner(out[1]))
print('--------------------------------------')
print('Input :', inputs[2])
print('hidden:', out[1])
print('Output:', liner(out[2]))
运行结果:
out tensor([[[ 2., 2.]],
[[ 6., 6.]],
[[16., 16.]]], grad_fn=<StackBackward0>) tensor([[[16., 16.]]], grad_fn=<StackBackward0>)
Input : tensor([[1., 1.]])
hidden: 0 0
Output: tensor([[4., 4.]], grad_fn=<AddmmBackward0>)
--------------------------------------
Input : tensor([[1., 1.]])
hidden: tensor([[2., 2.]], grad_fn=<SelectBackward0>)
Output: tensor([[12., 12.]], grad_fn=<AddmmBackward0>)
--------------------------------------
Input : tensor([[2., 2.]])
hidden: tensor([[6., 6.]], grad_fn=<SelectBackward0>)
Output: tensor([[32., 32.]], grad_fn=<AddmmBackward0>)
4. 分析“二进制加法” 源代码(选做)
import copy, numpy as np
np.random.seed(0)
# compute sigmoid nonlinearity
def sigmoid(x):
output = 1 / (1 + np.exp(-x))
return output
# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
return output * (1 - output)
# training dataset generation
int2binary = {}
binary_dim = 8
largest_number = pow(2, binary_dim)
binary = np.unpackbits(
np.array([range(largest_number)], dtype=np.uint8).T, axis=1)
for i in range(largest_number):
int2binary[i] = binary[i]
# input variables
alpha = 0.1
input_dim = 2
hidden_dim = 16
output_dim = 1
# initialize neural network weights
synapse_0 = 2 * np.random.random((input_dim, hidden_dim)) - 1
synapse_1 = 2 * np.random.random((hidden_dim, output_dim)) - 1
synapse_h = 2 * np.random.random((hidden_dim, hidden_dim)) - 1
synapse_0_update = np.zeros_like(synapse_0)
synapse_1_update = np.zeros_like(synapse_1)
synapse_h_update = np.zeros_like(synapse_h)
# training logic
for j in range(10000):
# generate a simple addition problem (a + b = c)
a_int = np.random.randint(largest_number / 2) # int version
a = int2binary[a_int] # binary encoding
b_int = np.random.randint(largest_number / 2) # int version
b = int2binary[b_int] # binary encoding
# true answer
c_int = a_int + b_int
c = int2binary[c_int]
# where we'll store our best guess (binary encoded)
d = np.zeros_like(c)
overallError = 0
layer_2_deltas = list()
layer_1_values = list()
layer_1_values.append(np.zeros(hidden_dim))
# moving along the positions in the binary encoding
for position in range(binary_dim):
# generate input and output
X = np.array([[a[binary_dim - position - 1], b[binary_dim - position - 1]]])
y = np.array([[c[binary_dim - position - 1]]]).T
# hidden layer (input ~+ prev_hidden)
layer_1 = sigmoid(np.dot(X, synapse_0) + np.dot(layer_1_values[-1], synapse_h))
# output layer (new binary representation)
layer_2 = sigmoid(np.dot(layer_1, synapse_1))
# did we miss?... if so, by how much?
layer_2_error = y - layer_2
layer_2_deltas.append((layer_2_error) * sigmoid_output_to_derivative(layer_2))
overallError += np.abs(layer_2_error)
# decode estimate so we can print it out
d[binary_dim - position - 1] = np.round(layer_2[0][0])
# store hidden layer so we can use it in the next timestep
layer_1_values.append(copy.deepcopy(layer_1))
future_layer_1_delta = np.zeros(hidden_dim)
for position in range(binary_dim):
X = np.array([[a[position], b[position]]])
layer_1 = layer_1_values[-position - 1]
prev_layer_1 = layer_1_values[-position - 2]
# error at output layer
layer_2_delta = layer_2_deltas[-position - 1]
# error at hidden layer
layer_1_delta = (future_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(
synapse_1.T)) * sigmoid_output_to_derivative(layer_1)
# let's update all our weights so we can try again
synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
synapse_0_update += X.T.dot(layer_1_delta)
future_layer_1_delta = layer_1_delta
synapse_0 += synapse_0_update * alpha
synapse_1 += synapse_1_update * alpha
synapse_h += synapse_h_update * alpha
synapse_0_update *= 0
synapse_1_update *= 0
synapse_h_update *= 0
# print out progress
if (j % 1000 == 0):
print("Error:" + str(overallError))
print("Pred:" + str(d))
print("True:" + str(c))
out = 0
for index, x in enumerate(reversed(d)):
out += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out))
print("------------")
运行结果:
Error:[[3.45638663]]
Pred:[0 0 0 0 0 0 0 1]
True:[0 1 0 0 0 1 0 1]
9 + 60 = 1
------------
Error:[[3.63389116]]
Pred:[1 1 1 1 1 1 1 1]
True:[0 0 1 1 1 1 1 1]
28 + 35 = 255
------------
Error:[[3.91366595]]
Pred:[0 1 0 0 1 0 0 0]
True:[1 0 1 0 0 0 0 0]
116 + 44 = 72
------------
Error:[[3.72191702]]
Pred:[1 1 0 1 1 1 1 1]
True:[0 1 0 0 1 1 0 1]
4 + 73 = 223
------------
Error:[[3.5852713]]
Pred:[0 0 0 0 1 0 0 0]
True:[0 1 0 1 0 0 1 0]
71 + 11 = 8
------------
Error:[[2.53352328]]
Pred:[1 0 1 0 0 0 1 0]
True:[1 1 0 0 0 0 1 0]
81 + 113 = 162
------------
Error:[[0.57691441]]
Pred:[0 1 0 1 0 0 0 1]
True:[0 1 0 1 0 0 0 1]
81 + 0 = 81
------------
Error:[[1.42589952]]
Pred:[1 0 0 0 0 0 0 1]
True:[1 0 0 0 0 0 0 1]
4 + 125 = 129
------------
Error:[[0.47477457]]
Pred:[0 0 1 1 1 0 0 0]
True:[0 0 1 1 1 0 0 0]
39 + 17 = 56
------------
Error:[[0.21595037]]
Pred:[0 0 0 0 1 1 1 0]
True:[0 0 0 0 1 1 1 0]
11 + 3 = 14
------------
RNN主要学两件事,一个是前一位的进位,一个是当前位的加法操作。只告诉当前阶段和前一阶段的计算结果,让网络自己学习加法和进位操作。
Anyone Can Learn To Code an LSTM-RNN in Python (Part 1: RNN) - i am trask
5. 实现“Character-Level Language Models”源代码(必做)
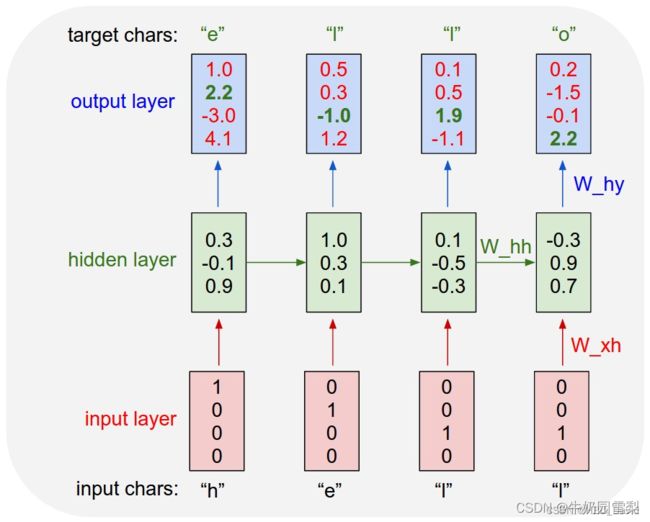
翻译Character-Level Language Models 相关内容
The Unreasonable Effectiveness of Recurrent Neural Networks
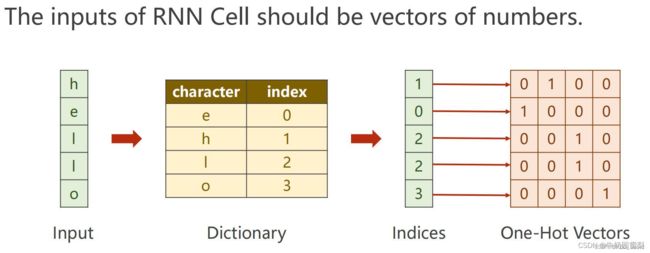
- 假设我们只有四个可能字母“helo”的词汇表,并且想要在训练序列“hello”上训练一个RNN。这个训练序列实际上是4个独立训练示例的来源:1.给定“h”的上下文,“e”的概率应该是可能的,2。“l”在“he”的上下文中应该是可能的,3。“l”也应该有可能给定“hel”的上下文,最后是4。“o”应该可能是给定“地狱”的上下文。具体地说,我们将使用1/k编码将每个字符编码成一个向量(即,除了词汇表中字符索引处的单个字符外,所有字符都为零),并使用step函数一次一个地将它们输入RNN。然后,我们将观察一个四维输出向量序列(每个字符一维),我们将其解释为RNN当前分配给序列中下一个字符的置信度。
- 没有序列的顺序处理。您可能会认为将序列作为输入或输出可能相对较少,但需要认识的重要一点是,即使您的输入/输出是固定向量,仍然可以使用这种强大的形式主义以顺序方式处理它们。
编码实现该模型
# coding=gbk
import torch
# 使用RNN 有嵌入层和线性层
num_class = 4 # 4个类别
input_size = 4 # 输入维度是4
hidden_size = 8 # 隐层是8个维度
embedding_size = 10 # 嵌入到10维空间
batch_size = 1
num_layers = 2 # 两层的RNN
seq_len = 5 # 序列长度是5
# 准备数据
idx2char = ['e', 'h', 'l', 'o'] # 字典
x_data = [[1, 0, 2, 2, 3]] # hello 维度(batch,seqlen)
y_data = [3, 1, 2, 3, 2] # ohlol 维度 (batch*seqlen)
inputs = torch.LongTensor(x_data)
labels = torch.LongTensor(y_data)
# 构造模型
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.emb = torch.nn.Embedding(input_size, embedding_size)
self.rnn = torch.nn.RNN(input_size=embedding_size, hidden_size=hidden_size, num_layers=num_layers,
batch_first=True)
self.fc = torch.nn.Linear(hidden_size, num_class)
def forward(self, x):
hidden = torch.zeros(num_layers, x.size(0), hidden_size)
x = self.emb(x) # (batch,seqlen,embeddingsize)
x, _ = self.rnn(x, hidden)
x = self.fc(x)
return x.view(-1, num_class) # 转变维2维矩阵,seq*batchsize*numclass -》((seq*batchsize),numclass)
model = Model()
# 损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.05) # lr = 0.01学习的太慢
# 训练
for epoch in range(15):
optimizer.zero_grad()
outputs = model(inputs) # inputs是(seq,Batchsize,Inputsize) outputs是(seq,Batchsize,Hiddensize)
loss = criterion(outputs, labels) # labels是(seq,batchsize,1)
loss.backward()
optimizer.step()
_, idx = outputs.max(dim=1)
idx = idx.data.numpy()
print("Predicted:", ''.join([idx2char[x] for x in idx]), end='')
print(",Epoch {}/15 loss={:.3f}".format(epoch + 1, loss.item()))
运行结果:
Predicted: leeel,Epoch 1/15 loss=1.494
Predicted: lllll,Epoch 2/15 loss=1.202
Predicted: lllll,Epoch 3/15 loss=1.040
Predicted: ollol,Epoch 4/15 loss=0.872
Predicted: ohlol,Epoch 5/15 loss=0.634
Predicted: ohlol,Epoch 6/15 loss=0.433
Predicted: ohlol,Epoch 7/15 loss=0.297
Predicted: ohlol,Epoch 8/15 loss=0.202
Predicted: ohlol,Epoch 9/15 loss=0.138
Predicted: ohlol,Epoch 10/15 loss=0.096
Predicted: ohlol,Epoch 11/15 loss=0.068
Predicted: ohlol,Epoch 12/15 loss=0.049
Predicted: ohlol,Epoch 13/15 loss=0.036
Predicted: ohlol,Epoch 14/15 loss=0.027
Predicted: ohlol,Epoch 15/15 loss=0.021
6. 分析“序列到序列”源代码(选做)
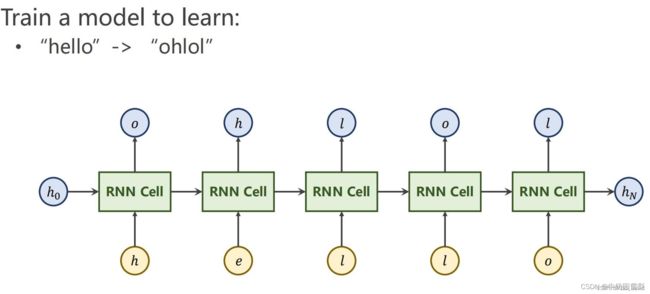
h0相当于初始隐状态输入,h是正常的输入,1、2、3、4分别是不同的隐状态进入到下一个RNN Cell中去,由上一个的隐状态向量和当前输入确定当前输出和隐状态向量输出,从而将“hello”翻译成了"ohlol".
# Model
class Seq2Seq(nn.Module):
def __init__(self):
super(Seq2Seq, self).__init__()
self.encoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # encoder
self.decoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # decoder
self.fc = nn.Linear(n_hidden, n_class)
def forward(self, enc_input, enc_hidden, dec_input):
# enc_input(=input_batch): [batch_size, n_step+1, n_class]
# dec_inpu(=output_batch): [batch_size, n_step+1, n_class]
enc_input = enc_input.transpose(0, 1) # enc_input: [n_step+1, batch_size, n_class]
dec_input = dec_input.transpose(0, 1) # dec_input: [n_step+1, batch_size, n_class]
# h_t : [num_layers(=1) * num_directions(=1), batch_size, n_hidden]
_, h_t = self.encoder(enc_input, enc_hidden)
# outputs : [n_step+1, batch_size, num_directions(=1) * n_hidden(=128)]
outputs, _ = self.decoder(dec_input, h_t)
model = self.fc(outputs) # model : [n_step+1, batch_size, n_class]
return model
model = Seq2Seq().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
#下面是训练,由于输出的 pred 是个三维的数据,所以计算 loss 需要每个样本单独计算,因此就有了下面 for 循环的代码
for epoch in range(5000):
for enc_input_batch, dec_input_batch, dec_output_batch in loader:
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
h_0 = torch.zeros(1, batch_size, n_hidden).to(device)
(enc_input_batch, dec_intput_batch, dec_output_batch) = (enc_input_batch.to(device), dec_input_batch.to(device), dec_output_batch.to(device))
# enc_input_batch : [batch_size, n_step+1, n_class]
# dec_intput_batch : [batch_size, n_step+1, n_class]
# dec_output_batch : [batch_size, n_step+1], not one-hot
pred = model(enc_input_batch, h_0, dec_intput_batch)
# pred : [n_step+1, batch_size, n_class]
pred = pred.transpose(0, 1) # [batch_size, n_step+1(=6), n_class]
loss = 0
for i in range(len(dec_output_batch)):
# pred[i] : [n_step+1, n_class]
# dec_output_batch[i] : [n_step+1]
loss += criterion(pred[i], dec_output_batch[i])
if (epoch + 1) % 1000 == 0:
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
seq2seq(sequence to sequence)模型是NLP中的一个经典模型,基于RNN网络模型构建,用途非常广泛:语言翻译,人机对话,问答系统等。
Seq2Seq,就如字面意思,输入一个序列,输出另一个序列,比如在机器翻译中,输入英文,输出中文。这种结构最重要的地方在于输入序列和输出序列的长度是可变的。而Seq2Seq模型也经常在输出的长度不确定时采用。
7. “编码器-解码器”的简单实现(必做)

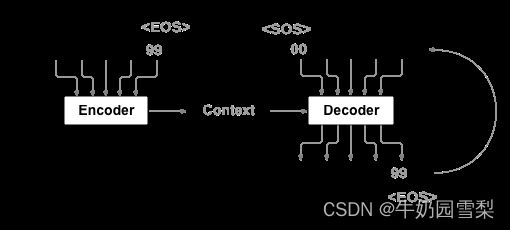
首先,从上面的图可以很明显的看出,Seq2Seq 需要对三个变量进行操作,这和之前我接触到的所有网络结构都不一样。我们把 Encoder 的输入称为 enc_input,Decoder 的输入称为 dec_input, Decoder 的输出称为 dec_output。下面以一个具体的例子来说明整个 Seq2Seq 的工作流程。
# coding=gbk
# code by Tae Hwan Jung(Jeff Jung) @graykode, modify by wmathor
import torch
import numpy as np
import torch.nn as nn
import torch.utils.data as Data
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# S: Symbol that shows starting of decoding input
# E: Symbol that shows starting of decoding output
# ?: Symbol that will fill in blank sequence if current batch data size is short than n_step
letter = [c for c in 'SE?abcdefghijklmnopqrstuvwxyz']
letter2idx = {n: i for i, n in enumerate(letter)}
seq_data = [['man', 'women'], ['black', 'white'], ['king', 'queen'], ['girl', 'boy'], ['up', 'down'], ['high', 'low']]
# Seq2Seq Parameter
n_step = max([max(len(i), len(j)) for i, j in seq_data]) # max_len(=5)
n_hidden = 128
n_class = len(letter2idx) # classfication problem
batch_size = 3
def make_data(seq_data):
enc_input_all, dec_input_all, dec_output_all = [], [], []
for seq in seq_data:
for i in range(2):
seq[i] = seq[i] + '?' * (n_step - len(seq[i])) # 'man??', 'women'
enc_input = [letter2idx[n] for n in (seq[0] + 'E')] # ['m', 'a', 'n', '?', '?', 'E']
dec_input = [letter2idx[n] for n in ('S' + seq[1])] # ['S', 'w', 'o', 'm', 'e', 'n']
dec_output = [letter2idx[n] for n in (seq[1] + 'E')] # ['w', 'o', 'm', 'e', 'n', 'E']
enc_input_all.append(np.eye(n_class)[enc_input])
dec_input_all.append(np.eye(n_class)[dec_input])
dec_output_all.append(dec_output) # not one-hot
# make tensor
return torch.Tensor(enc_input_all), torch.Tensor(dec_input_all), torch.LongTensor(dec_output_all)
'''
enc_input_all: [6, n_step+1 (because of 'E'), n_class]
dec_input_all: [6, n_step+1 (because of 'S'), n_class]
dec_output_all: [6, n_step+1 (because of 'E')]
'''
enc_input_all, dec_input_all, dec_output_all = make_data(seq_data)
class TranslateDataSet(Data.Dataset):
def __init__(self, enc_input_all, dec_input_all, dec_output_all):
self.enc_input_all = enc_input_all
self.dec_input_all = dec_input_all
self.dec_output_all = dec_output_all
def __len__(self): # return dataset size
return len(self.enc_input_all)
def __getitem__(self, idx):
return self.enc_input_all[idx], self.dec_input_all[idx], self.dec_output_all[idx]
loader = Data.DataLoader(TranslateDataSet(enc_input_all, dec_input_all, dec_output_all), batch_size, True)
# Model
class Seq2Seq(nn.Module):
def __init__(self):
super(Seq2Seq, self).__init__()
self.encoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # encoder
self.decoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # decoder
self.fc = nn.Linear(n_hidden, n_class)
def forward(self, enc_input, enc_hidden, dec_input):
# enc_input(=input_batch): [batch_size, n_step+1, n_class]
# dec_inpu(=output_batch): [batch_size, n_step+1, n_class]
enc_input = enc_input.transpose(0, 1) # enc_input: [n_step+1, batch_size, n_class]
dec_input = dec_input.transpose(0, 1) # dec_input: [n_step+1, batch_size, n_class]
# h_t : [num_layers(=1) * num_directions(=1), batch_size, n_hidden]
_, h_t = self.encoder(enc_input, enc_hidden)
# outputs : [n_step+1, batch_size, num_directions(=1) * n_hidden(=128)]
outputs, _ = self.decoder(dec_input, h_t)
model = self.fc(outputs) # model : [n_step+1, batch_size, n_class]
return model
model = Seq2Seq().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(5000):
for enc_input_batch, dec_input_batch, dec_output_batch in loader:
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
h_0 = torch.zeros(1, batch_size, n_hidden).to(device)
(enc_input_batch, dec_intput_batch, dec_output_batch) = (
enc_input_batch.to(device), dec_input_batch.to(device), dec_output_batch.to(device))
# enc_input_batch : [batch_size, n_step+1, n_class]
# dec_intput_batch : [batch_size, n_step+1, n_class]
# dec_output_batch : [batch_size, n_step+1], not one-hot
pred = model(enc_input_batch, h_0, dec_intput_batch)
# pred : [n_step+1, batch_size, n_class]
pred = pred.transpose(0, 1) # [batch_size, n_step+1(=6), n_class]
loss = 0
for i in range(len(dec_output_batch)):
# pred[i] : [n_step+1, n_class]
# dec_output_batch[i] : [n_step+1]
loss += criterion(pred[i], dec_output_batch[i])
if (epoch + 1) % 1000 == 0:
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Test
def translate(word):
enc_input, dec_input, _ = make_data([[word, '?' * n_step]])
enc_input, dec_input = enc_input.to(device), dec_input.to(device)
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
hidden = torch.zeros(1, 1, n_hidden).to(device)
output = model(enc_input, hidden, dec_input)
# output : [n_step+1, batch_size, n_class]
predict = output.data.max(2, keepdim=True)[1] # select n_class dimension
decoded = [letter[i] for i in predict]
translated = ''.join(decoded[:decoded.index('E')])
return translated.replace('?', '')
print('test')
print('man ->', translate('man'))
print('mans ->', translate('mans'))
print('king ->', translate('king'))
print('black ->', translate('black'))
print('up ->', translate('up'))
运行结果:
Epoch: 1000 cost = 0.002338
Epoch: 1000 cost = 0.002321
Epoch: 2000 cost = 0.000495
Epoch: 2000 cost = 0.000492
Epoch: 3000 cost = 0.000147
Epoch: 3000 cost = 0.000157
Epoch: 4000 cost = 0.000053
Epoch: 4000 cost = 0.000051
Epoch: 5000 cost = 0.000018
Epoch: 5000 cost = 0.000019
test
man -> women
mans -> women
king -> queen
black -> white
up -> down
总结
这次作业我们使用numpy实现了一个SRN,已有的SRN基础上加入了激活函数,分别使用nn.RNNCell、nn.RNN实现SRN,分析“二进制加法” 源代码,实现“Character-Level Language Models”源代码,分析“序列到序列”源代码,简单实现编码器-解码器,明白了RNN和RNNCell的区别与联系以及他们的含义,收获了很多。
参考
Seq2Seq 的 PyTorch 实现
完全图解RNN、RNN变体、Seq2Seq、Attention机制