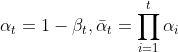【Paper Notes】Denoising Diffusion Probabilistic Models
近来Diffusion Model在数据生成领域取得了很重要的进展，比如DALLE-2，和google的imagen等，效果非常惊人。因此有必要学习一下这个方法。
Diffusion Model的基本过程
Diffusion Model 有两个基本过程，分为前向（forward diffusion process) 和逆向（reverse diffusion process).
前向过程，是向图像
中不断加入噪声
。直到数据完全退化成高斯噪声
。
逆向过程，是向由噪声,不断预测加入的噪声，一步一步恢复出的过程。
Diffusion Model 基本过程
我们可以用公式化的描述来理解这个过程。
Forward
注意等式右边两项的参数的平方和是1，这是一个有意的设计。原因是？请先思考，文末有答案。
并且，
一般都取比较小的数字，比如0.001，这是为了保证其逆向过程也近似为正态分布。
Reverse
在reverse过程中，我们一般通过一个UNet来对
进行建模。
训练目标函数
清晰了diffusion model的基本过程，那么就会出现一个问题，如何训练这个UNet？
最简单的方法就是，根据Forward过程，采样得到
,然后直接求解出
,如下所示：
但是这个过程显然不够高效，因为每次训练之前，都得执行一遍完整的Forward Process。因此需要考虑更高效的训练方式，如果可以直接用训练，不用执行forward过程是最好的。
递推关系
这里可以先推导
的关系。
首先令 
, 根据公式（1）可以得到：
其中，最后一步是根据两个高斯分布相加，还是高斯分布，并且其均值是两个分布的均值之和，新的方差是两个分布方差之和。
根据上式，可以得到
训练目标简化
我们将（4）式直接带入 （3）式，可以得到
这样的话，其实每次只需要采样
就可以（其实有点问题，
可能不互相独立），但是这需要采样两次，还没有达到最优，最优情况下只需要采样一次，并且需要采样两个高维随机变量，可能会导致训练不稳定，难以收敛。因此还需要对式子进行化简。
我们采用
来进行递推。
可以得到，
到这里如何进一步化简呢？
我们令
因此，可以得到，注意
并不独立？
又因为，在计算损失时，我们通常考虑期望，即
![L_{obj} = E_{\bold{w}, \bold{s}}\big[||\frac{\sqrt{1-\bar\alpha_t}}{2\sqrt{1-\alpha_t}}(\bold{w}-\bold{s}) - \epsilon_{\theta}(\sqrt{\bar\alpha_t}\bold{x}_0 + \sqrt{1-\bar\alpha_t}\bold{w},t) ||^2\big]](http://img.e-com-net.com/image/info8/d324ae11272d4f5ba3a1095efb5cfcf7.gif){kind=small}
并且，
只包含二次项和一次项，所以在忽略常数的情况下，等价于优化
上述推导有点问题，越推导越感觉不对，先贴出目前比较认可的损失函数：
训练过程
有了以上训练目标函数，和forward process的定义，那么训练和采样过程也非常简洁易懂。
问题回答
为什么，在Forward过程中要约束两个系数的平方和为1呢？
在处理图像的时候，我们会对图像做mean和std变换。变换后可以将每个像素的分布看作一个N(0,1)的正态分布。那么如果两个正太分布直接相加，其期望不会发生变化，但是方差会变为两个分布的方差之和。为此需要约束两个系数的平方和为1，这样两个分布相加后其期望还是1.