深度学习入门之多维数组运算
深度学习入门之多维数组运算
参考书籍:深度学习入门——基于pyhthon的理论与实现
文章目录
- 深度学习入门之多维数组运算
- 前言
- 一、多维数组是什么?
- 二、矩阵乘法
- 三、神经网络内积
- 总结
前言
对于实现神经网络,学会使用numpy多维数组的使用是必须的。多维数组简单地讲就是‘数字的集合’,数字排一列的集合、排成行乘列的长方形集合、排成长乘宽乘高的立方体形状,或者说N维状的集合都称为多维数组。
一、多维数组是什么?
N维状的集合称为多维数组,由numpy生成多维数组的过程如下:
代码如下(示例):
import numpy as np
A = np.array([1,2,3,4,5,6])
print(A)
#输出
>[1 2 3 4 5 6]
np.ndim(A)
>1
A.shape
>(6,)
A.shape[0]
>6
数组的维数可以使用np.ndim()函数进行查看,获取数组形状可以利用实例变量shape获取,上述程序中,A为一个一维数组,由6个元素构成,A.shape返回的结果是一个元组,这是因为一维数组的情况也要返回和多维数组的情况一致的格式,所以返回的结果结构和多为数组一致。例如,二维数组返回的元组是(4,3),三维数组返回的元组是(4,3,2)。二维数组如下:
代码如下(示例):
import numpy as np
b=np.array([[1,2],[3,4],[5,6]])
print(b)
print(np.ndim(b))
print(b.shape)
#输出结果
>[[1 2]
[3 4]
[5 6]]
>2
>(3,2)
这里生成了一个3x2的二维数组,3x2表示第一个维度有3个元素,第二个维度有2个元素。第一个维度对应第0维,第二个维度对应第1维(python的索引从0开始)。二维数组也称为矩阵(matrix)。

数组的横向排列称为行(row),纵向排列称为列(column)。
二、矩阵乘法
下面简单介绍一下矩阵乘法,计算过程如下所示:

矩阵的乘积是通过左边矩阵的行和右边的列以对应元素相乘再求和得到,运算的结果保存为新的多维数组,运算过程就像上图流程一样。
python代码实现如下所示:
代码如下(示例):
import numpy as np
a=np.array([[1,2],[3,4])
print(a.shape)
b=np.array([[5,6],[7,8]])
print(b.shape)
c=np.dot(a,b)
print(c)
#输出结果
>(2,2)
>(2,2)
>array([[19 22],
[43,50]])
上面的代码展示了2x2矩阵的乘法运算,其他矩阵的运算也是一致的。注意的是矩阵左乘和矩阵右乘的结果是不一样的,也就是说np.dot(a,b)和np.dot(b,a)两个结果是完全不一样的。numpy中的np.dot()函数(乘积计算也称点积),np.dot()函数接收两个numpy数组作为输入,并返回数组的乘积结果。
代码如下(示例):
import numpy as np
a=array([[1 2 3],[4 5 6]])
print(a.shape)
b=array([[1 2],[3 4],[5 6]])
print(b.shape)
c=np.dot(a,b)
#输出结果
>(2,3)
>(3,2)
>array([[22 28],
[49,64]])
矩阵相乘需要满足一定的条件,也就是乘积的第一个数组的列数,也就是第二个维度(第1维)的维数要和第二个数组的行数,也就是第一维度(第0维)的维数要一致。
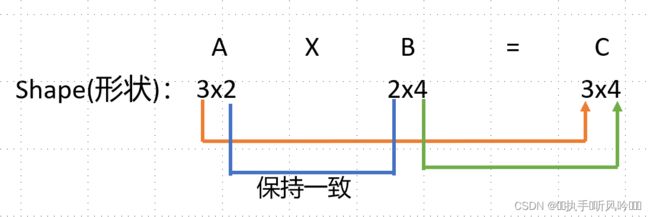
保持一致:表示该位置上的数值要一模一样,不能不一致,否则程序会报错,矩阵运算出错。
三、神经网络内积
下面我们使用numpy矩阵来实现神经网络,这里以简单神经网络为对象,这个神经网络省略了偏置参数和激活函数,只有权重参数。如下图所示:
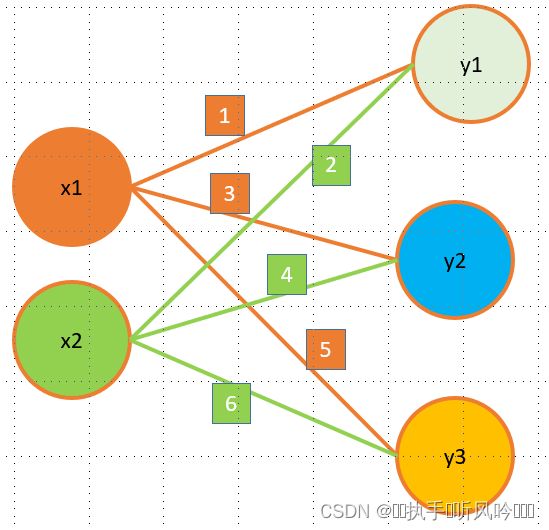
该网络表示两个输入,三个输出,其中方块中的数值表示对应的输入对应输出的权重参数。运算过程如下图所示:
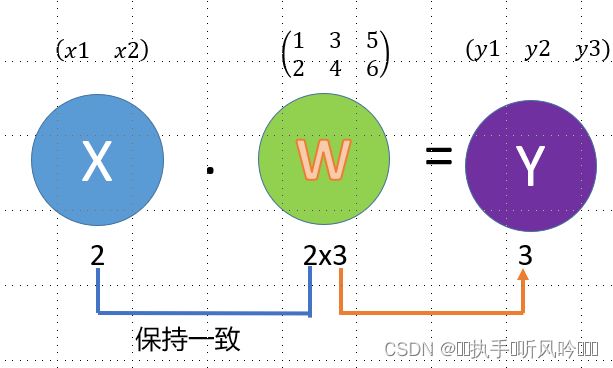
实行按神经网络时,一定要注意X、W、Y的形状,特别是X和W的对应的维度的元素需要一致,X的第1维数应该等于W的第0维数,即X的列数应该等于W的行数。
通过python程序表述的话,如下图所示:
import numpy as np
x=np.array([1,2])
w=np.array([[1,3,5],[2,4,6]])
print(x.shape)
print(w.shape)
y=np.dot(x.w)
print(y)
#输出结果
#只有一维数组表示有点特殊
>(2,)
>(2,3)
>[5 11 17]
np.dot()多维数组的点积,可以一次性计算出Y的结果,不管Y的元素个数是多少,只要在计算机承受范围内,也可以一次性计算,通过矩阵的一次性乘积对于实现的层面上可以说非常重要。
总结
主要简单介绍了一下矩阵在numpy乘积运算中的一个过程以及运算需要注意的几个小技巧。