机器学习笔记（李宏毅 2021/2022）——第二节：机器学习攻略任务

相关视频（B站）

2021-机器学习攻略任务
2021-类神经网络训练不起来怎么办（一）局部最小值和鞍点
2021-类神经网络训练不起来怎么办（二）批次与动量
2021-类神经网络训练不起来怎么办（三）自动调整学习率
2021-类神经网络训练不起来怎么办（四）损失函数也可能有影响
2021-类神经网络训练不起来怎么办（五）批次标准化
2022-再谈宝可梦、数码宝贝分类器-浅谈机器学习原理

一、2021-机器学习攻略任务

这节主要讲了在训练深度学习模型时，应该怎样做

1.检查Training Data 的loss

首先我们应该检查Training Data 的loss，因为如果Training Data 的loss就很大，那就证明它在训练集里就没有训练好。这里有两个原因。

1.1.Model Bias（偏差）

Model Bias的原因往往是模型弹性不够大，需要重新设计一个弹性更大的Model。

1.2.Optimization Issue

还有一种可能是Optimization做的差，即梯度下降遇到了问题。想大海捞针,针确实在海裡,但是我们却没有办法把针捞起来。

1.3.如何区分是Model Bias还是Optimization Issue？

一个建议判断的方法,就是你可以透过比较不同的模型，来得知说，你的model现在到底够不够大。

• 首先跑一些较小的network，或者甚至不使用DP（因为小模型往往比较好optimize），得到loss。
  ——即先有个概念，小model的loss大概多少

• 然后比较大模型，如果大模型的loss大，说明Optimization遇到问题了。（因为大模型的弹性一定好，原理上把后几层的w设为1，b设为0，就是小模型）

2.检查 Testing Data的loss

假设你现在经过一番的努力,你已经可以让你的，training data的loss变小了，那接下来你就可以来看，testing data loss,如果testing data loss也小，有比这个strong baseline还要小就结束了，没什麼好做的，就结束了。
但如果不够小，情况是training data上面的loss小，testing data上的loss大，那你可能就是遇到overfitting的问题。

2.1.如何解决overfitting

• 增加训练集
• 给模型增加限制（减少参数、Dropout、减少feature、Regularization、early stop）

2.2.Mismatch

事实上，还有一种可能是遇到了mismatch。mismatch意思是说，你今天的训练集跟测试集，它们的分布是不一样的。

3.数据集分为Train\Dev\Test的原因

因为kaggle有两个数据集用于评价模型的好坏，分别为Public和Private。在竞赛时间内，只能知道自己的Public分数，无法知道Private的分数。
而当我们把Training的资料分为Train和Dev时，

• 用Train训练，
• 用Val验证模型的好坏

那么kaggle中的public分数就可以反应private的分数了。

4.N-fold Cross Validation

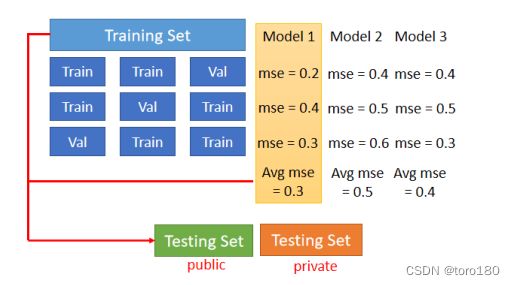
N-fold Cross Validation就是你先把你的训练集切成N等份,在这个例子裡面我们切成三等份,切完以后,你拿其中一份当作Validation Set,另外两份当Training Set,然后这件事情你要重复三次。
也就是说,你先第一份第二份当Train,第三份当Validation,然后第一份第三份当Train,第二份当Validation,第一份当Validation,第二份第三份当Train。
然后接下来 你有三个模型,你不知道哪一个是好的,你就把这三个模型,在这三个setting下,在这三个Training跟Validation的data set上面,通通跑过一次,然后把这三个模型,在这三种状况的结果都平均起来,把每一个模型在这三种状况的结果,都平均起来,再看看谁的结果最好。
那假设现在model 1的结果最好,你用这三个fold得出来的结果是,这个model 1最好,然后你再把model1,用在全部的Training Set上,然后训练出来的模型,再用在Testing Set上面,那这个便是N-fold CrossValidation。

二、类神经网络训练不起来怎么办

1.局部最小值（local minima）和鞍点（saddle point）

首先，这两个都叫做Critical point。（Critical point指梯度为0的点）

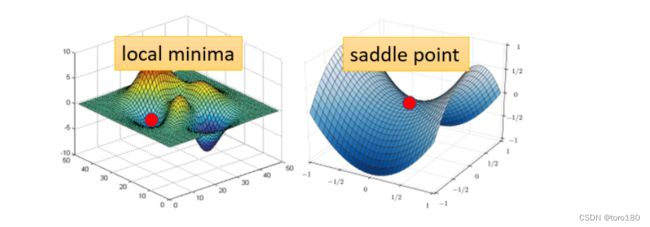
其次，為什麼我们想要知道到底是卡在local minima,还是卡在saddle point呢？

• 因為如果是卡在local minima,那可能就没有路可以走了,因為四周都比较高,你现在所在的位置已经是最低的点,loss最低的点了,往四周走loss都会比较高,你会不知道怎麼走到其他的地方去
• 但saddle point就比较没有这个问题,如果你今天是卡在saddle point的话,saddle point旁边还是有路可以走的,还是有路可以让你的loss更低的,你只要逃离saddle point,你就有可能让你的loss更低

然后，我们要怎么判断是local mimima还是saddle point呢？（这里省略一大推数学推导，直接记录结论）

• 你只要算出一个东西,这个东西的名字叫做 hessian,它是一个矩阵,这个矩阵如果它所有的eigen value,都是正的,那就代表我们现在在local minima,如果它有正有负,就代表在saddle point。

最后，其实判断并不重要。

• loacl minima为假问题。由于深度学习的参数很多，维度很高，从低维的空间来看,是没有路可以走的东西,在高维的空间中是有路可以走的，所以一般在DP中不会出现local minima的问题
• saddle point有许多方法可以逃离，且运算量比算Hessian更小。（比如small batch、momentum）

2.批次（batch）与动量（momentum）

2.1.batch

这里直接记录不同batch的结果。

• 由于平行化计算的原因，large batch计算完整一个epoch的时间更短
• small batch的噪声更大，但正是由于噪声的原因能够帮助模型走出saddle point，更好的optimize
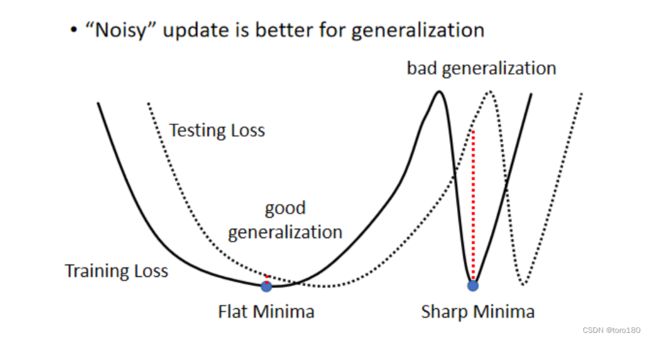
• small batch的泛化效果更好（大的 Batch Size,会让我们倾向於走到峡谷裡面,而小的 Batch Size,倾向於让我们走到盆地裡面）
  

2.2.momentum

momentum是另一个有助于对抗saddle point或者local minima的方法。
简单理解就是惯性，给梯度下降加了一个动量，在梯度为0的地方仍有之前留下来的动量，如果动量足够大，就能走出critical point。

3.自动调整学习率（Adaptive learning rate）

3.1.loss不下降时，gradient不一定很小

当我们说走到critical point的时候,意味著gradient非常的小,但是你有确认过,当你的loss不再下降的时候,gradient真的很小吗？其实多数的同学可能,都没有确认过这件事,而事实上在这个例子裡面,在今天我show的这个例子裡面,当我们的loss不再下降的时候,gradient并没有真的变得很小。

这个是我们的error surface,然后你现在的gradient,在error surface山谷的两个谷壁间,不断的来回的震荡。

3.2.参数客制化

在之前我们的gradient descend裡面,所有的参数都是设同样的learning rate,这显然是不够的,learning rate它应该要為,每一个参数客製化,所以接下来我们就是要讲,客製化的learning rate,怎麼做到这件事情。
这是原来的更新梯度公式：

现在我们把它改成这样：

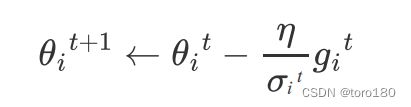
$\sigma$的常见计算方式有以下几种。

• Root mean square
  
  这招被用在Adagrad的方法里，但并非现在的常用方法。

• RMSprop
  
  那这个α就像learning rate一样,这个你要自己调它,它是一个hyperparameter
  ——如果我今天α设很小趋近於0,就代表我觉得gᵢ¹相较於之前所算出来的gradient而言,比较重要
  ——我α设很大趋近於1,那就代表我觉得现在算出来的gᵢ¹比较不重要,之前算出来的gradient比较重要

3.3.Adam

现如今常用的optimizer之一Adam，就是RMSprop+Momentum。今天pytorch里已经把它封装好了，往往不调整参数，使用默认参数就能有不错的效果。
adam原始论文

3.4.Learning rate scheduling

• 左上右上的图均采用恒定的learning rate，一个比较大，一个比较小
• 右下的图采用adagrad训练十万次

原本模型train不起来，那现在有Adagrad以后,你可以再继续走下去,走到非常接近终点的位置,因為当你走到这个地方的时候,你因為这个左右的方向的,这个gradient很小,所以learning rate会自动调整,左右这个方向的,learning rate会自动变大,所以你这个步伐就可以变大,就可以不断的前进。
But 接下来的问题就是,為什麼快走到终点的时候突然爆炸了呢？
Because纵轴一直有累积小的grad，当到达一定程度，纵轴方向的$\sigma$就会变得
很小，就会突然爆炸。
这时候就需要learning rate scheduling了。
learning rate scheduling的意思就是说,我们不要把η当一个常数,我们把它和时间挂钩。

• 最常见的策略叫做Learning Rate Decay,也就是说，随著时间的不断地进行,随著参数不断的update,我们这个η让它越来越小。
• 还有一种叫warm up，这Warm Up的方法是让learning rate,要先变大后变小
  （简单理解是以一开始learning rate比较小,是让它探索收集一些有关error surface的情报,先收集有关σ的统计数据,等σ统计得比较精準以后,在让learning rate呢慢慢地爬升）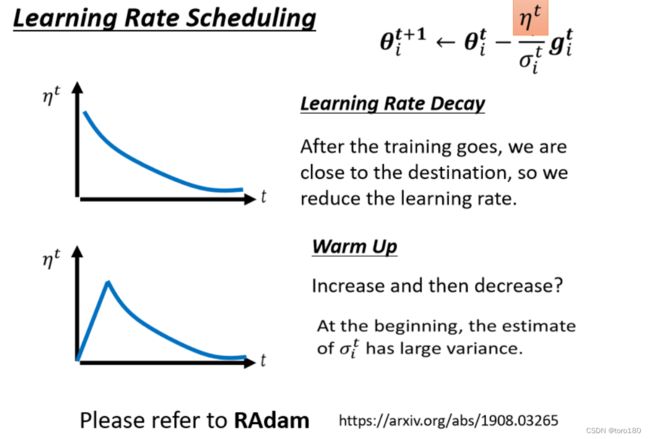

3.5 可能的困惑

Q、一个momentum是考虑过去所有的gradient,这个σ也是考虑过去所有的gradient,一个放在分子一个放在分母,都考虑过去所有的gradient,不就是正好抵销了吗？
A、其实不然，momentum是带方向的，而σ是标量仅仅影响大小，不考虑方向。

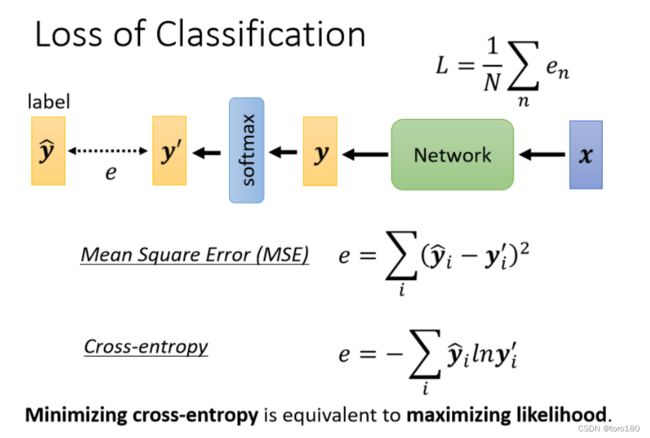
4.损失函数（loss）也可能有影响

这节李宏毅老师主要是通介绍了Classification相关问题，同时指出了交叉熵和MSE对optimize的影响。

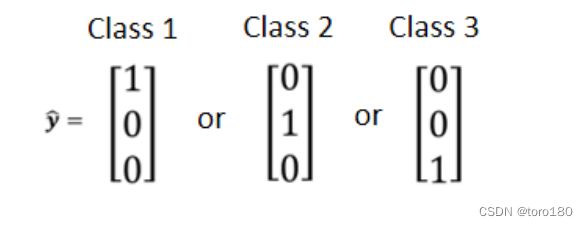
4.1. One-hot vector（独热编码）

采用独热编码的好处是，不同class之间的距离是一样的。

4.2.softmax

公式：

图示化：

• yi’都是介於0到1之间
• yi’的和是1
• 让大的值和小的值差距更大
• 两个class的softmax和sigmoid一样

4.3 cross-entropy

• 在分类问题中，cross-entropy更加适用。
• 在Pytorch中，cross-entropy和softmax被绑定在一起了，也就是说如果使用了cross-entropy作为损失函数，就不用显式的添加softmax了。
• 在分类问题中，cross-entropy的error surface更加平缓
  

5.批次标准化（batch normalization）

Batch Normalization 是另一种把error surface弄平缓的方式。

5.1.feature normalization

假设x1到xr ,是我们所有的训练资料的 feature vector。

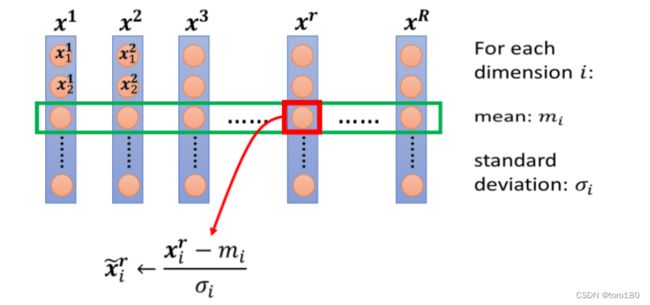
这里取的是不同训练资料中同一维度的数据归一化。
好处：

• 做完 normalize 以后啊,这个 dimension 上面的数值就会平均是 0,然后它的 variance就会是 1,所以这一排数值的分布就都会在 0 上下
• 对每一个 dimension都做一样的 normalization,就会发现所有 feature 不同 dimension 的数值都在 0 上下,那你可能就可以製造一个,比较好的 error surface

5.2. Batch normalization

考虑到hidden layer中的输出同样有不同的范围，那么是不是对hidden layer的输出也进行归一化会有好处呢？

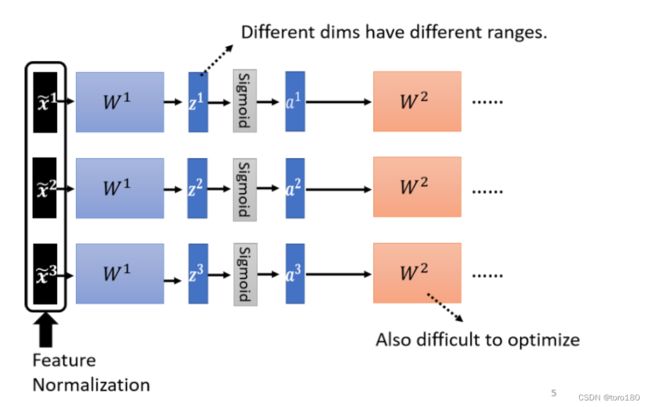
所以就有了Batch normalization。取一个batch中的中间层数据计算均值和方差。（一般如果激活函数是sigmoid的话，在激活函数之前做归一化有利于梯度下降，因为sigmoid在0附近斜率大）

在实作的时候,你不会让这一个 network 考虑整个 training data 裡面的所有 example,你只会考虑一个batch 裡面的 example,举例来说,你 batch 设 64,那你这个巨大的 network,就是把 64 笔 data 读进去,算这 64 笔 data 的 ,算这 64 笔 data 的 ,对这 64 笔 data 都去做 normalization。
因為我们在实作的时候,我们只对一个 batch 裡面的 data,做 normalization,所以这招叫做 Batch Normalization。

3.3.可能的问题

假设你真的有系统上线,你是一个真正的线上的 application,比如说你的 batch size 设 64,我一定要等 64 笔资料都进来,我才一次做运算吗,这显然是不行的。

所以真正的,这个实作上的解法是这个样子的,如果你看那个 PyTorch 的话呢,Batch Normalization 在testing 的时候,你并不需要做什麼特别的处理,PyTorch 帮你处理好了
在 training 的时候,如果你有在做 Batch Normalization 的话,在 training 的时候,你每一个 batch 计算出来的 μ跟 σ,他都会拿出来算 moving average。

三、浅谈机器学习原理

这一节内容主要阐述了模型理想（在所有数据中）和现实（仅有训练数据集）的差距和相关原理。

首先，为了简化内容，把模型函数写为一个threshold函数，且h仅能取【1，10000】，这个意思就是仅有10000个候选函数。

但我们只能从所有数据集中取出一部分作为训练集进行训练，毕竟绝大多数情况下，我们无法获得所有数据。
现在我们希望现实和理想的loss可以比较接近。

而这就需要训练的数据集尽量接近所有数据。
课程给出，满足上式公式的训练集是所有数据的好的代言。

• 取任一h，都能满足训练模型的loss和完美情况的loss的差值<=$\delta$/2

通过Hoeffding’s Inequality公式，我们可以推导出训练集是坏的概率小于等于下式（此处省略了推导步骤）

所以说，为了让训练集坏的概率尽量低，我们需要Larger N and smaller |H|，也就是说更大的数据集，更小的模型弹性（即模型的可选择项少）。

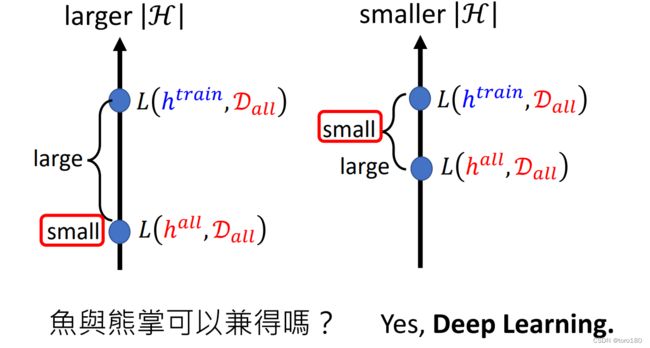
那如果我们选择Larger N and smaller |H|，其实仍然存在有问题。

• 如果我们选择了弹性大的模型，那么我们理想的loss会很低，但是理想和现实的差距会比较大
• 如果我们选择了弹性小的模型，那我们虽然理想和现实的差距小，但是理想的loss本来就不小

能不能鱼与熊掌兼得呢？
可以，使用Deep Learning！