cs224w(图机器学习)2021冬季课程学习笔记14 Reasoning over Knowledge Graphs
诸神缄默不语-个人CSDN博文目录
cs224w(图机器学习)2021冬季课程学习笔记集合
VX号“PolarisRisingWar”可直接搜索添加作者好友讨论。
更新日志:删除PPT链接
文章目录
- 1. Reasoning over Knowledge Graphs
- 2. Answering Predictive Queries on Knowledge Graphs
- 3. Query2box: Reasoning over KGs Using Box Embeddings
- 4. 本章总结
- 5. 其他正文及脚注未提及的参考资料
YouTube 视频观看地址1 视频观看地址2 视频观看地址3
本章主要内容:
本章将介绍知识图谱上的推理任务。
目标是回答 多跳查询multi-hop queries,包括path queries和conjunctive queries。
conjunctive合取的,交集的;与;连接的;联合的,连接(着)的; 契合的;逻辑乘法的
介绍query2box方法以解决predictive queries问题。
1. Reasoning over Knowledge Graphs
- 回忆:知识图谱补全任务1
- 本章主旨:介绍如何实现知识图谱上的多跳推理任务。
- 知识图谱示例:Biomedicine(以下课程内容都会使用这个知识图谱来作为示例)
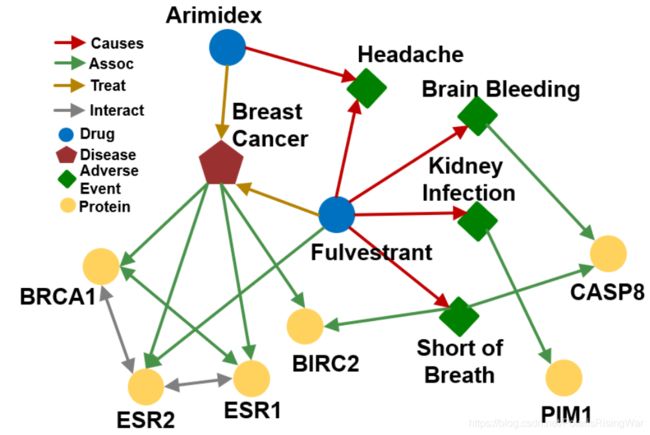
- KG上的predictive queries
任务目标:在一个incomplete的大型KG上做多跳推理(如回答复杂查询问题)。
对于某一类查询,我们可以自然语言的形式(绿色字)、formula/logical structure(棕色字)的形式或者graph structure(蓝色节点是查询中出现的实体,绿色节点是查询结果)的形式来表示它。
本节课仅讨论有formula/logical structure或graph structure后如何进行工作,从自然语言转换到对应形式的工作不在本课程讲解。
查询类型及示例:- one-hop queries
What adverse event is caused by Fulvestrant?
(e:Fulvestrant, (r:Causes))

- path queries
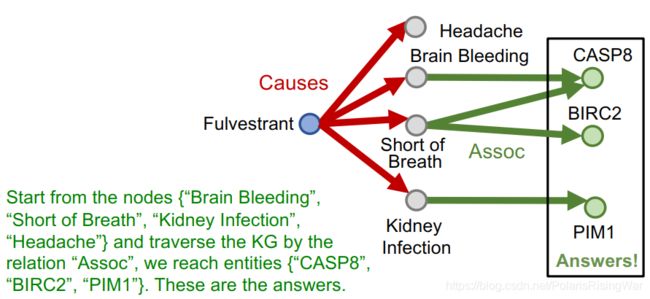
What protein is associated with the adverse event caused by Fulvestrant?
(e:Fulvestrant, (r:Causes, r:Assoc))
- conjunctive queries
What is the drug that treats breast cancer and caused headache?
((e:BreastCancer, (r:TreatedBy)), (e:Migraine, (r:CausedBy))

- one-hop queries
- predictive one-hop queries
知识图谱补全任务可以formulate成回答one-hop queries问题:
KG补全任务:链接 ( h , r , t ) (h,r,t) (h,r,t) 在KG中是否存在?
one-hop query: t t t 是否是查询 ( h , ( r ) ) (h,(r)) (h,(r)) 的答案?
举例:What side effects are caused by drug Fulvestrant?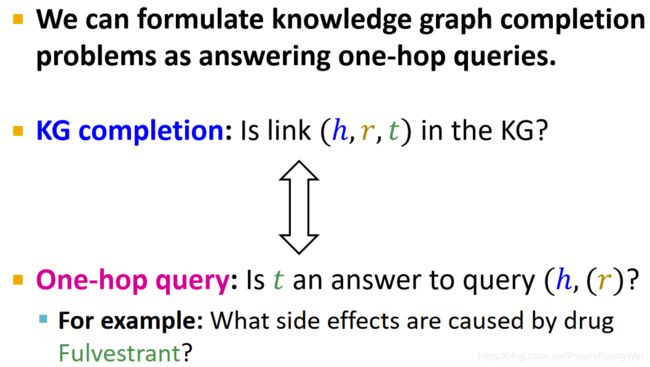 图中那个查询应该是少写了一个右括号
图中那个查询应该是少写了一个右括号 - path queries
one-hop queries可以视作path queries的特殊情况,one-hop queries在路径上增加更多关系就成了path queries。
一个n-hop query q q q 可表示为: q = ( v a , ( r 1 , … , r n ) ) q=(v_a,(r_1,\dots,r_n)) q=(va,(r1,…,rn))
v a v_a va 是 anchor entity
查询结果可表示为 ⟦ q ⟧ G \llbracket q\rrbracket_G [[q]]G
q q q 的query plan(一个链):


path queries示例:What proteins are associated with adverse events caused by Fulvestrant?
v a v_a va 是 e:Fulvestrant
( r 1 , r 2 ) (r_1,r_2) (r1,r2) 是 (r:Causes, r:Assoc)
query:(e:Fulvestrant, (r:Causes, r:Assoc))
query plan:

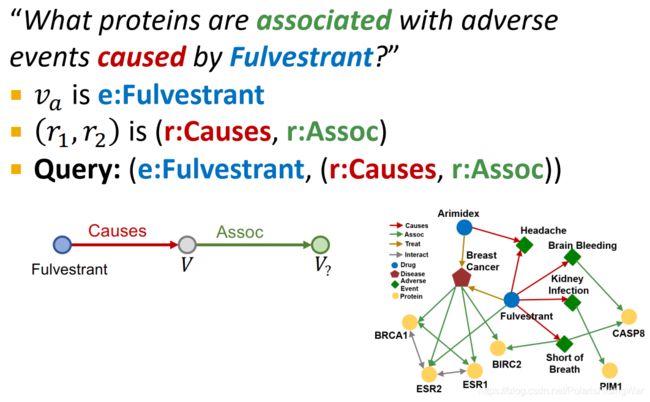
- 那么我们应该如何回答KG上的path query问题呢?
如果图是complete的话,那么我们只需要沿query plan直接traverse(遍历)KG就可以。 - 但由于KG是incomplete的,所以如果仅traverse KG,可能会缺失一些关系,从而无法找到全部作为答案的实体。

- 我们可能很直觉地会想,那能不能直接先用KG补全技术,将KG补全为completed (probabilistic) KG,然后再traverse KG?
但这样不行,KG被补全后就会是一个稠密图,因为KG补全后很多关系存在的概率都非0,所以KG上会有很多关系,在traverse时要过的边太多,其复杂度与路径长度 L L L 呈指数增长: O ( d m a x L ) O(d^L_{max}) O(dmaxL) ,复杂度过高,无法实现。
- 因此我们就需要进行预测任务:predictive queries
目标:在incomplete KG上回答path-based queries
我们希望这一方法能够回答任意查询问题,同时隐式地impute或补全KG,实现对KG中缺失信息和噪音的鲁棒性。
对链接预测任务的泛化:从one-step link prediction task(就以前讲过的那种)到multi-step link prediction task(path queries)
2. Answering Predictive Queries on Knowledge Graphs
- idea: traversing KG in vector space2
核心思想:嵌入query
相当于把TransE1 泛化到multi-hop reasoning任务上:使query embedding q \mathbf{q} q(相当于一个实体加关系的嵌入: q = h + r \mathbf{q}=\mathbf{h}+\mathbf{r} q=h+r) 与answer embedding t \mathbf{t} t(一个实体)靠近, f q ( t ) = − ∣ ∣ q − t ∣ ∣ f_q(t)=-||\mathbf{q}-\mathbf{t}|| fq(t)=−∣∣q−t∣∣
对path query q = ( v a , ( r 1 , … , r n ) ) q=(v_a,(r_1,\dots,r_n)) q=(va,(r1,…,rn)),其嵌入就是 q = v a + r 1 + ⋯ + r n \mathbf{q}=\mathbf{v}_a+\mathbf{r}_1+\cdots+\mathbf{r}_n q=va+r1+⋯+rn
嵌入过程仅包含向量相加,与KG中总实体数无关。
path query示例: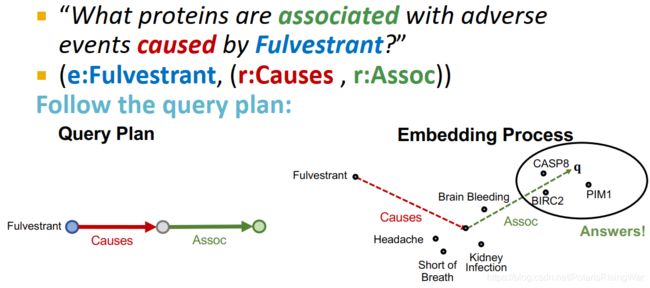
可以训练TransE来优化KG补全目标函数。
因为TransE天然可以处理composition relations,所以也能处理path queries,在隐空间通过叠加relation嵌入来表示多跳。
TransR / DistMult / ComplEx无法处理composition relations,因此很难像TransE这样轻易扩展到path queries上。
- conjunctive queries
示例:
What are drugs that cause Short of Breath and treat diseases associated with protein ESR2?
((e:ESR2, (r:Assoc, r:TreatedBy)), (e:Short of Breath, (r:CausedBy))
query plan:

- 同样,如果KG是complete的话,直接traverse KG就行:




- 同样,如果KG有关系缺失了,有些答案就会找不到:
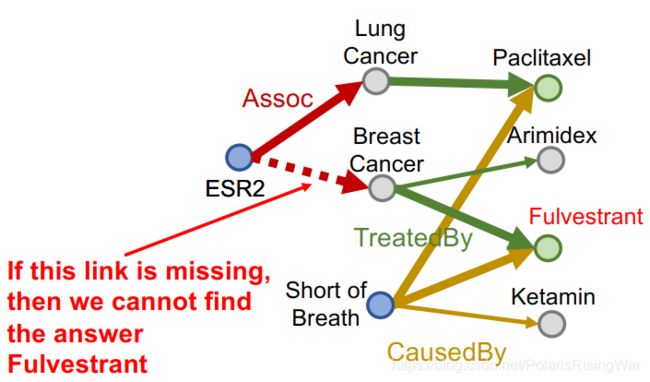
- 我们希望通过嵌入方法来隐式impute KG中缺失的关系 (ESR2, Assoc, Breast Cancer)。
如图所示,ESR2与BRCA1和ESR1都有interact关系,这两个实体都与breast cancer有assoc关系:
- 再回顾一遍query plan,注意图中的中间节点都代表实体,我们也需要学习这些实体的表示方法。此外我们还需要定义在隐空间的intersection操作。

3. Query2box: Reasoning over KGs Using Box Embeddings
- box embeddings3
用 hyper-rectangles (boxes) 来建模query: q = ( C e n t e r ( q ) , O f f s e t ( q ) ) \mathbf{q}=(Center(q),Offset(q)) q=(Center(q),Offset(q))
offset(在计算机里应该是偏移量的意思)
一个多维长方形,用中心和corner(偏移)来定义。
如图所示:在理想状态下,一个box里包含了所有query(Fulverstrant副作用)的回答的实体。
- key insight: intersection
box就是组合之后还是box,就很好定义节点集的intersection。
- embed with box embedding
- projection operator P \mathcal{P} P
用当前box作为输入,用关系嵌入来投影和扩展box,得到一个新的box。
P : Box × Relation → Box C e n ( q ′ ) = C e n ( q ) + C e n ( r ) O f f ( q ′ ) = O f f ( q ) + O f f ( r ) \mathcal{P}:\text{Box}\times\text{Relation}\rightarrow\text{Box} \\ Cen(q')=Cen(q)+Cen(r) \\ Off(q')=Off(q)+Off(r) P:Box×Relation→BoxCen(q′)=Cen(q)+Cen(r)Off(q′)=Off(q)+Off(r)
- 用box embedding,用projection operator,沿query plan求解:

- 接下来我们的问题就在于:如何定义box上的intersection?
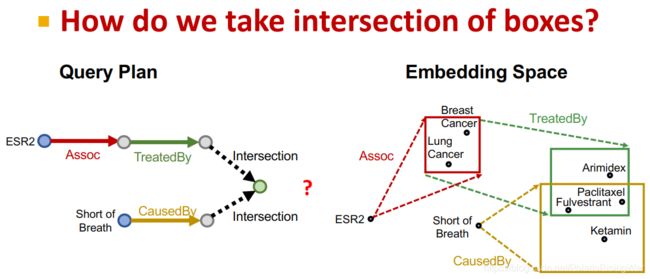 有一种对intersection的定义比较严格,就是定义为数学上的intersection,类似于维恩图。
有一种对intersection的定义比较严格,就是定义为数学上的intersection,类似于维恩图。
我们想要更flexible一点的定义,就如下文所介绍: - intersection operator
geometric intersection operator J \mathcal{J} J
输入:多个box
输出:intersection box
J : Box × ⋯ × Box → Box \mathcal{J}:\text{Box}\times\cdots\times\text{Box}\rightarrow\text{Box} J:Box×⋯×Box→Box
直觉: - intersection operator公式
- center
C e n ( q i n t e r ) = ∑ i w i ⊙ C e n ( q i ) w i = exp ( f c e n ( C e n ( q i ) ) ) ∑ j exp ( f c e n ( C e n ( q j ) ) ) Cen(q_{inter})=\sum_i\mathbf{w}_i\odot Cen(q_i) \\ \mathbf{w}_i=\frac{\exp\left(f_{cen}(Cen(q_i))\right)}{\sum_j\exp(f_{cen}(Cen(q_j)))} Cen(qinter)=i∑wi⊙Cen(qi)wi=∑jexp(fcen(Cen(qj)))exp(fcen(Cen(qi)))
(其中 ⊙ \odot ⊙是哈达玛积,即逐元素乘积。 C e n ( q i ) ∈ R d , w i ∈ R d Cen(q_i)\in\mathbb{R}^d,\mathbf{w}_i\in\mathbb{R}^d Cen(qi)∈Rd,wi∈Rd)
直觉解读:center应该在下图红色区域内(原center之间)
应用:center是原center的加权求和
w i ∈ R d \mathbf{w}_i\in\mathbb{R}^d wi∈Rd 通过含可训练参数的神经网络 f c e n f_{cen} fcen 计算得到,代表每个输入 C e n ( q i ) Cen(q_i) Cen(qi) 的self-attention得分。5
- offset
O f f ( q i n t e r ) = min ( O f f ( q 1 ) , … , O f f ( q n ) ) ⊙ σ ( f o f f ( O f f ( q 1 ) , … , O f f ( q n ) ) ) \begin{aligned} Off(q_{inter})=&\min(Off(q_1),\dots,Off(q_n)) \\ &\odot\sigma(f_{off}(Off(q_1),\dots,Off(q_n))) \end{aligned} Off(qinter)=min(Off(q1),…,Off(qn))⊙σ(foff(Off(q1),…,Off(qn)))
(保证offset收缩: σ \sigma σ 表示sigmoid函数,把输出压缩到 (0,1) 之间。 f o f f f_{off} foff 是一个含可训练参数的神经网络,提取input boxes的表示向量以增强表示能力)

- center
- 通过定义intersection operator,现在我们可以完成使用box embedding沿query plan的求解:

- entity-to-box distance
定义score function f q ( v ) \mathbf{f}_q(v) fq(v)(query box q q q 和 entity embedding v v v(也是个box)距离的相反数):
d b o x ( q , v ) = d o u t ( q , v ) + α ⋅ d i n ( q , v ) d_{box}(\mathbf{q},\mathbf{v})=d_{out}(\mathbf{q},\mathbf{v})+\alpha\cdot d_{in}(\mathbf{q},\mathbf{v}) dbox(q,v)=dout(q,v)+α⋅din(q,v)(其中 0 < α < 1 0<\alpha<1 0<α<1)
直觉:如果实体在盒子里面,距离权重就应该较小。
f q ( v ) = − d b o x ( q , v ) \mathbf{f}_q(v)=-d_{box}(\mathbf{q},\mathbf{v}) fq(v)=−dbox(q,v)
- extending to union operation
析取问题示例:What drug can treat breast cancer or lung cancer?
conjunctive queries + disjunction被叫做Existential Positive First-order (EPFO) queries,也叫AND-OR queries。
disjunction或6

- 在低维向量空间可以嵌入AND-OR queries吗?
答案是不能,在任意查询上的union操作必须要高维嵌入。- 举例:三个查询和对应的答案实体集合: ⟦ q 1 ⟧ = { v 1 } , ⟦ q 2 ⟧ = { v 2 } , ⟦ q 3 ⟧ = { v 3 } \llbracket q_1\rrbracket=\{v_1\},\llbracket q_2\rrbracket=\{v_2\},\llbracket q_3\rrbracket=\{v_3\} [[q1]]={v1},[[q2]]={v2},[[q3]]={v3}
如果我们允许union操作,可以将其嵌入到二维平面上吗?
以下图示中,红点(答案)是我们希望在box中的实体,蓝点(负答案)是我们希望在box外的实体:
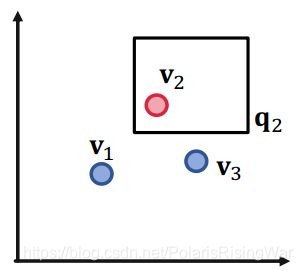

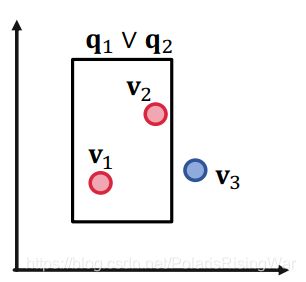


对三个点来说,二维是足够的。 - 举例:四个查询和对应的答案实体集合: ⟦ q 1 ⟧ = { v 1 } , ⟦ q 2 ⟧ = { v 2 } , ⟦ q 3 ⟧ = { v 3 } , ⟦ q 4 ⟧ = { v 4 } \llbracket q_1\rrbracket=\{v_1\},\llbracket q_2\rrbracket=\{v_2\},\llbracket q_3\rrbracket=\{v_3\},\llbracket q_4\rrbracket=\{v_4\} [[q1]]={v1},[[q2]]={v2},[[q3]]={v3},[[q4]]={v4}
如果我们允许union操作,可以将其嵌入到二维平面上吗?
答案是不能,举例来说,如下图所示,我们希望设计一个 q 2 ∨ q 4 \mathbf{q}_2\vee\mathbf{q}_4 q2∨q4 的box embedding,即 v 2 v_2 v2 和 v 4 v_4 v4 在box里, v 1 v_1 v1 和 v 3 v_3 v3 在box外。显然不行。
结论:任何 M M M 个conjunctive queries q 1 , … , q M q_1,\dots,q_M q1,…,qM ,各自答案不重叠,我们需要 Θ ( M ) \Theta(M) Θ(M) 维来处理所有 OR queries。这可能就很大。7
- 举例:三个查询和对应的答案实体集合: ⟦ q 1 ⟧ = { v 1 } , ⟦ q 2 ⟧ = { v 2 } , ⟦ q 3 ⟧ = { v 3 } \llbracket q_1\rrbracket=\{v_1\},\llbracket q_2\rrbracket=\{v_2\},\llbracket q_3\rrbracket=\{v_3\} [[q1]]={v1},[[q2]]={v2},[[q3]]={v3}
- 因为我们无法在低维空间嵌入 AND-OR queries,所以对这类问题,我们的处理思路就是把所有query plan前面的union操作单拎出来,只在最后一步进行union操作。
如图所示: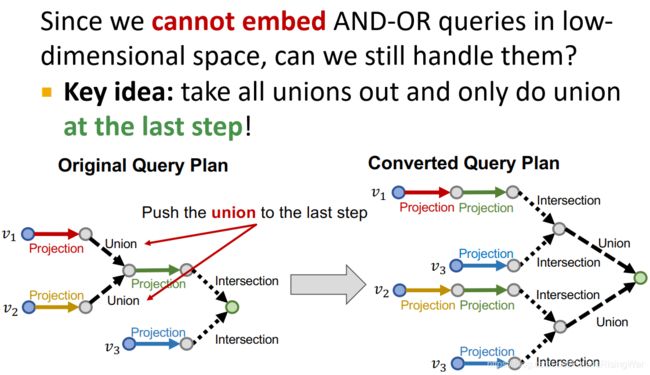
- disjunctive normal form (DNF)
AND-OR query可以表述成DNF的形式,例如conjunctive queries的disjunction:
q = q 1 ∨ q 2 ∨ ⋯ ∨ q m q=q_1\vee q_2\vee\cdots\vee q_m q=q1∨q2∨⋯∨qm
( q i q_i qi 是conjunctive query)
这样的话我们就可以先嵌入所有的 q i q_i qi,然后在最后一步聚集起来。

- 实体嵌入 v v v 和DNF q q q 之间的距离定义为: d b o x ( q , v ) = min ( d b o x ( q 1 , v ) , … , d b o x ( q m , v ) ) d_{box}(\mathbf{q},\mathbf{v})=\min(d_{box}(\mathbf{q_1},\mathbf{v}),\dots,d_{box}(\mathbf{q_m},\mathbf{v})) dbox(q,v)=min(dbox(q1,v),…,dbox(qm,v))
直觉: - 嵌入AND-OR query q q q 的过程
- 将 q q q 转换为 equivalent DNF q 1 ∨ q 2 ∨ ⋯ ∨ q m q_1\vee q_2\vee\cdots\vee q_m q1∨q2∨⋯∨qm
- 嵌入 q 1 q_1 q1 至 q m q_m qm
- 计算 (box) distance d b o x ( q i , v ) d_{box}(\mathbf{q}_i,\mathbf{v}) dbox(qi,v)
- 计算所有distance的最小值
- 得到最终score f q ( v ) = − d b o x ( q , v ) f_q(v)=-d_{box}(\mathbf{q},\mathbf{v}) fq(v)=−dbox(q,v)

- training overview
- overview and intuition(类似于KG补全问题)
已知query embedding q \mathbf{q} q
目标:最大化答案 v ∈ ⟦ q ⟧ v\in\llbracket q\rrbracket v∈[[q]] 上的得分 f q ( v ) f_q(v) fq(v),最小化负答案 v ′ ∉ ⟦ q ⟧ v'\not\in\llbracket q\rrbracket v′∈[[q]] 上的得分 f q ( v ′ ) f_q(v') fq(v′) - 可训练参数
- 实体嵌入参数量: d ∣ V ∣ d|V| d∣V∣
- 关系嵌入参数量: 2 d ∣ R ∣ 2d|R| 2d∣R∣
- intersection operator
- 接下来的问题就在于:如何从KG中获取query、query对应的答案和负答案来训练参数?如何划分KG?

- overview and intuition(类似于KG补全问题)
- 训练流程
- 从训练图 G t r a i n G_{train} Gtrain 中随机抽样一个query q q q,及其答案 v ∈ ⟦ q ⟧ v\in\llbracket q\rrbracket v∈[[q]] 和一个负答案样本 v ′ ∉ ⟦ q ⟧ v'\not\in\llbracket q\rrbracket v′∈[[q]]
负答案样本:在KG中存在且和 v v v 同类但非 q q q 答案的实体 - 嵌入query q \mathbf{q} q
- 计算得分 f q ( v ) f_q(v) fq(v) 和 f q ( v ′ ) f_q(v') fq(v′)
- 优化损失函数 l \mathcal{l} l以最大化 f q ( v ) f_q(v) fq(v) 并最小化 f q ( v ′ ) f_q(v') fq(v′):
l = − log σ ( f q ( v ) ) − log ( 1 − σ ( f q ( v ′ ) ) ) \mathcal{l}=-\log\sigma\big(f_q(v)\big)-\log(1-\sigma\big(f_q(v')\big)) l=−logσ(fq(v))−log(1−σ(fq(v′)))
- 从训练图 G t r a i n G_{train} Gtrain 中随机抽样一个query q q q,及其答案 v ∈ ⟦ q ⟧ v\in\llbracket q\rrbracket v∈[[q]] 和一个负答案样本 v ′ ∉ ⟦ q ⟧ v'\not\in\llbracket q\rrbracket v′∈[[q]]
- 抽样query:从templates生成
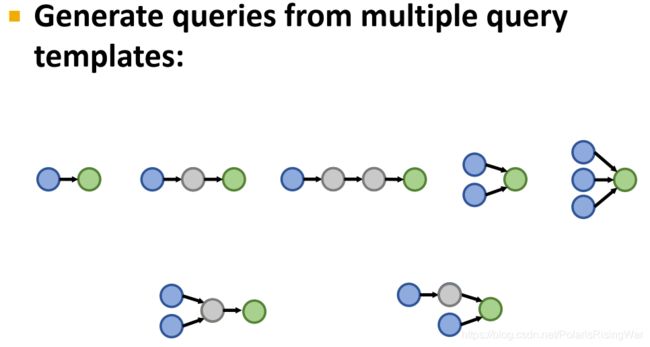
- 生成复杂query的流程:从query template开始,通过实例化query template中的变量为KG中实际存在的实体和关系来生成query(如实例化Anchor1为KG节点ESR2,Rel1为KG边Assoc)。
query template可以视作是query的抽象。
如图所示:

- 实例化query template的具体方法:从实例化答案节点开始,迭代实例化其他边和节点,直至到达8所有anchor nodes

- 实例化query template示例:
从query template的根节点开始:从KG中随机选择一个实体作为根节点,例如我们选择了Fulverstrant
然后我们看intersection:实体集的intersection是Fulverstrant,则两个实体集自然都应包含Fulverstrant
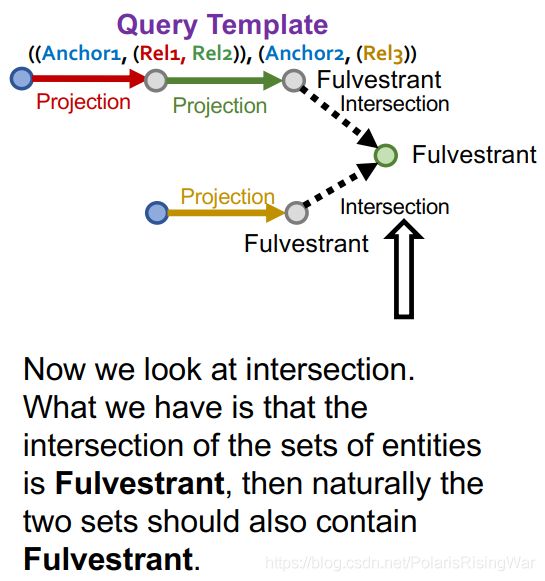
我们通过随机抽样一个连接到当前实体Fulverstrant的关系,来实例化对应的projection edge。举例来说,我们选择关系TreatedBy,检查通过TreatedBy关系连接到Fulverstrant的实体:{Breast Cancer}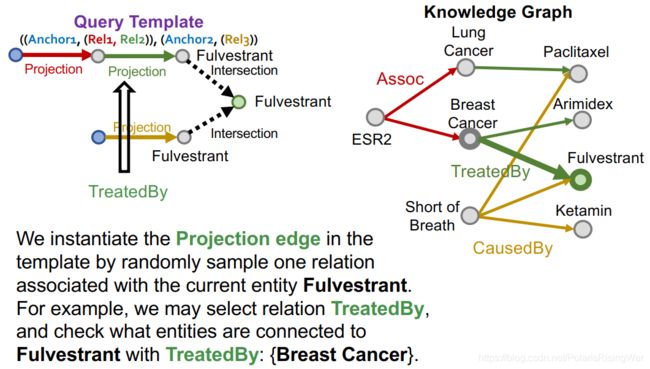
以此类推,完成一条支路:
类似地,完成另一条支路:

现在我们就得到了一个查询 q q q : ((e:ESR2, (r:Assoc, r:TreatedBy)), (e:Short of Breath, (r:CausedBy))
q q q 在KG上必有答案,而且其答案之一就是实例化的答案节点:Fulverstrant。
我们可以通过KG traversal获得全部答案集合 ⟦ q ⟧ G \llbracket q\rrbracket_G [[q]]G
抽样回答不了这个answer的节点作为 non-answer负样本 v ′ ∉ ⟦ q ⟧ G v'\not\in\llbracket q\rrbracket_G v′∈[[q]]G
- 在嵌入域可视化查询答案
示例:List male instrumentalists who play string instruments
用t-SNE将嵌入向量降维到2维

可视化节点嵌入和query plan:

anchor node的嵌入:

投影:

投影:

anchor node的嵌入:

投影:

intersection:
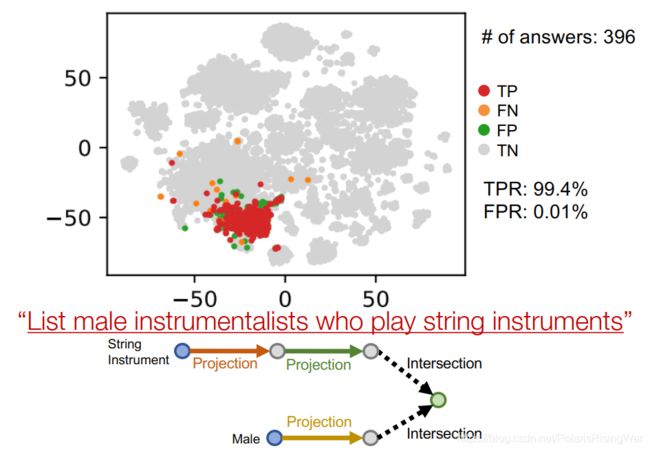
4. 本章总结
本章介绍了在大型KG上回答predictive queries。
关键思想在嵌入查询,通过可学习的operator来实现嵌入。在嵌入域中,query的嵌入应该靠近其答案的嵌入。
5. 其他正文及脚注未提及的参考资料
- 知识图谱推理:查询问句的艺术 - 知乎
可参考我之前撰写的博文:cs224w(图机器学习)2021冬季课程学习笔记12 Knowledge Graph Embeddings ↩︎ ↩︎
Guu, et al., Traversing knowledge graphs in vector space, EMNLP 2015 ↩︎
Ren et al., Query2box: Reasoning over Knowledge Graphs in Vector Space Using Box Embeddings, ICLR 2020 ↩︎
这个relation embedding为什么是2d的维度呢,我也没想清楚。我去瞅了一眼论文,就直接说是2d的维度了,但是没讲为啥。 ↩︎
为什么这么算,我感觉就是这样直接理解的话也可以,虽然我感觉好像这样解释没有讲清楚。
权重就是权重,为什么非要叫什么attention,self-attention的…… ↩︎关于disjunction是逻辑或,可以参考这个知乎问题:为什么“disjunction”(析取)是逻辑或? - 知乎
 ↩︎
↩︎话说这个从直觉到结论是怎么直接就推出来的……反正也没说 ↩︎
这里用的动词是ground,我就没搞懂它实际上是啥意思?就意译了 ↩︎