CS224W图神经网络笔记自用：Graph Neural Networks

1. 前言

1.1 Recap: Node Embeddings

思想：学习映射函数$f$，将节点映射到d维的嵌入向量中，让在图中相似的节点在嵌入空间同样紧密相连


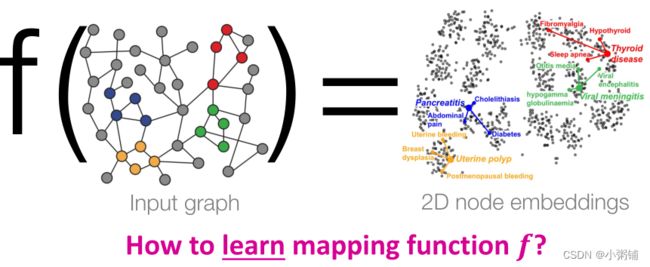
在学习节点嵌入时，有两个重要的部分：

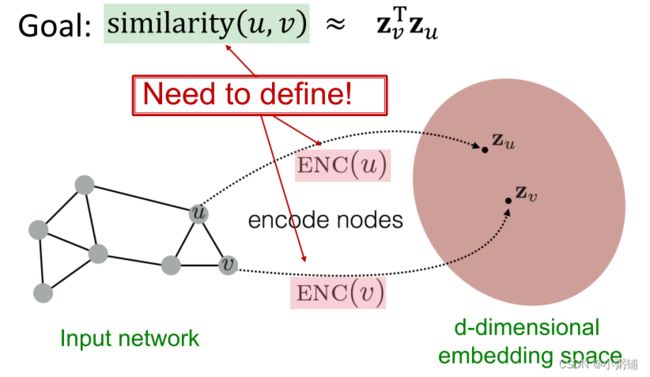
• 编码器（Encoder）：将每个节点v映射到一个低维向量$z_v$
  $$ENC(v)=z_v$$
• 相似性函数（解码器？）:指定向量空间中的关系如何映射到原始网络中的关系
  
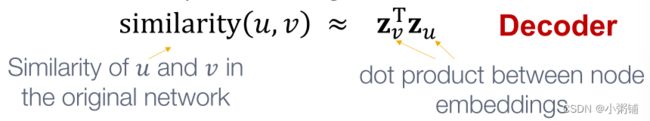
  ”浅“编码器：最简单的编码方法是编码器只是一个embedding-lookup
  
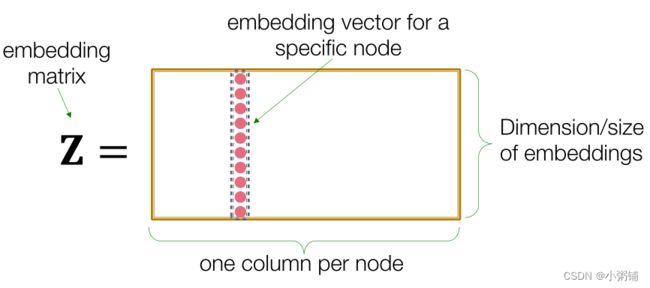
  ”浅“编码方法的局限：
• 一个需要$O(|V|)$个参数，模型的参数于网络中节点的数量成正比
  • 节点之间不共享参数
  • 每个节点都有自己独特的嵌入
• 本质上是“传递的”：无法为训练过程中新加入的节点生成嵌入
• 不包含节点特征：许多图中的节点具有我们应该利用的特征信息。

1.2 Deep Graph Encoders

今天的学习内容：基于图神经网络（GNNS) 的 深度图编码器（Deep Graph Encoders） : 基于图结构的多层非线性变换

注：所有这些深度编码器都可以和章节三的节点相似性函数结合（例如与用随机游走定义的相似性函数结合）
深度图编码器：

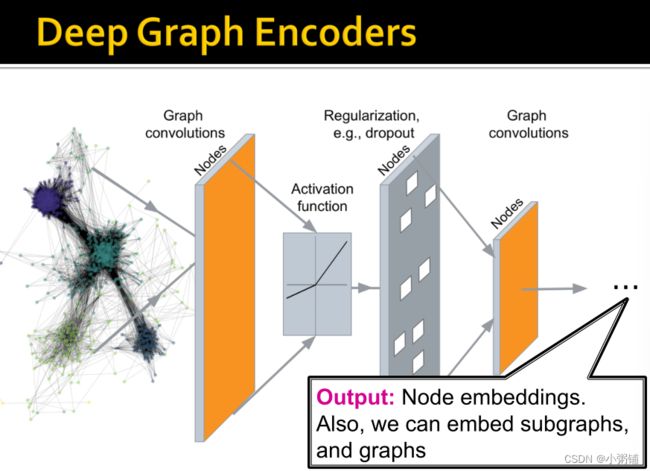
根据基于GNNS的深度图编码器，我们将解决以下问题：

• 节点分类：预测给定节点的类型
• 链接预测：预测两个节点是否链接
• 社区检测：识别密集链接的节点群
• 网络相似性：测量两个子图的相似性

现有的机器学习工具箱和深度学习工具箱都是为简单的序列数据和grids数据设计的，但是网络要比这种类型的数据复杂得多。

• 图有任意大小和复杂的拓扑结构(例如，不像网格那样具有空间局域性)
• 图没有固定的节点排序或参考点
• 图通常是动态的，具有多模态特征
  

1.3 Outline

1. 深度学习基础知识
2. 图的深度学习
3. 图卷积网络
4. GNNS VS. CNNs and Transformers

2. Basics of Deep Learning

2.1 Machine Learning as Optimization

监督学习（Supervised learning）：给定输入$x$,目标是预测标签$y$。
输入$x$可以有多种形式：

• 实数向量
• 序列（自然语言处理）
• 矩阵（图片）
• 图（节点和边的特征）

监督学习本质上是一个优化问题。 目标函数是：
$$min\mathcal{L}(y,f(x))$$
$\Theta$：是一组我们需要优化的参数

• 可以包含一个或多个标量、向量、矩阵…
• 例如：在浅编码器（the embedding lookup）中 $\Theta =\{Z\}$

ℒ: 损失函数，用于衡量真实标签和预测标签之间的差距，如L2 loss。
$$\mathcal{L}(y,(f(x))=|y-f(x)|{|}_2$$
其他常见的损失函数包括： L1 loss, huber loss, max margin (hinge loss), cross entropy … 等

2.2 损失函数

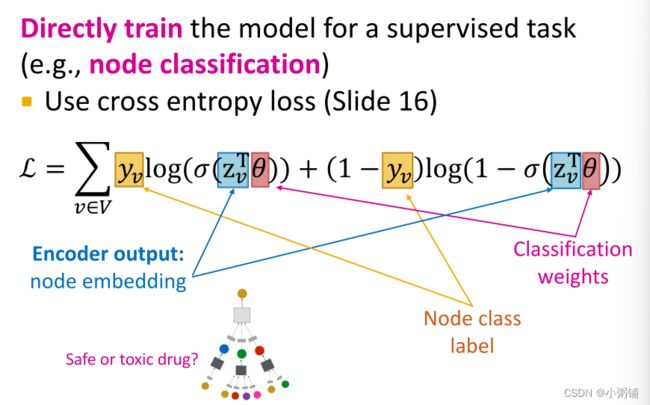
在分类问题中常见的损失函数是交叉熵损失函数（cross entropy / CE):

• 标签$y$是一个分类向量（独热编码）
  

• $f(x)=Softmax(g(x))$
  $$f(x{)}_i=\frac{e^{g(x{)}_i}}{{\sum }_{j=1}^C{e}^{g(x{)}_j}}$$
  其中，C是类别的数量，$g(x{)}_i$是函数$g(x)$的输出向量的第i个值。

• $CE(y,f(x))=-{\sum }_{i=1}^C(y_{i}logf(x{)}_i)$
  其中，$y_i$和$f(x{)}_i$是第i类的实际值和预测值。损失越低，预测越接近独热向量$y$

• 所有训练数据集的总损失如下，T是训练数据集：
  $$L=\sum _{(x,y)\in T}CE(y,f(x))$$

2.3 优化目标函数

那我们如何优化目标函数呢？
我们可以采用梯度下降（Gradient descent） 的方法，梯度向量代表了最快增长的方向和速率，如下：
梯度是最大增加方向上的方向导数。

2.3.1 Gradient Descent（梯度下降法）

梯度下降法是一种迭代算法，它沿梯度的（相反）方向重复更新权重，直到收敛：
$$\Theta \leftarrow \Theta -\eta {\nabla }_{\Theta }L$$
训练时，我们迭代优化参数$\Theta$，每次迭代梯度下降一步，$\eta$是学习率，是控制步长大小的超参数，可以在训练过程中调整，训练的理想终止条件是梯度为0，但是在实践中，如果训练不再提高验证集（我们从训练中保留的数据集的一部分）的性能，我们就将停止训练。

2.3.2 随机梯度下降（Stochastic Gradient Descent）

梯度下降法存在以下问题：

• 要求得精确的梯度需要计算${\nabla }_{\Theta }(y,f(x))$，其中$x$是整个数据集。
  • 这意味着对数据集中所有点的梯度贡献求和
  • 现代数据集通常都非常大，包含数十亿个数据点
  • 对于每个梯度下降步骤都非常昂贵

解决方法：随机梯度下降法（SGD）

• 在每一步，选择一个不同的小批量$B$(数据集的子集)，将其用作输入$x$。
  批量大小：小批量$B$中数据点的数量
  迭代（Iteration）：小批量上SGD的1步
  Epoch：数据集的一次完整传递（迭代次数等于数据集大小与批量大小的比）

如果我们创建的小批量是均匀随机分布的，那么SGD是整个梯度的无偏估计，但它不能保证收敛速度，在实践中经常需要调整学习率，常见的优化SGD算法的优化器有：Adam，Adagrad，Adadelta，RMSprop等

2.4 神经网络函数

目标：$mi{n}_{\Theta }L(y,f(x))$
在深度学习中，函数$f$可能非常复杂：

• 假如f是一个线性函数
  $$f(x)=W\cdot x,\Theta =\{W\}$$
  如果f函数返回一个标量，那么那么$W$就是一个可学习的向量：
  $${\nabla }_{W}f=(\frac{\partial f}{\partial w_1},\frac{\partial f}{\partial w_2},\frac{\partial f}{\partial w_3}...)$$
  如果f返回一个向量，那么W就是一个权重矩阵(右边为函数f的雅各比矩阵）:
  $${\nabla }_{W}f=\left[\begin{array}{cc}\frac{\partial f}{\partial w_{11}}& \frac{\partial f}{\partial w_{12}}\\ \frac{\partial f}{\partial w_{21}}& \frac{\partial f}{\partial w_{22}}\end{array}\right]$$

2.5 反向传播

反向传播：
对于复杂的函数，我们使用链式规则传播中间步骤的梯度，最终获得L关于$\Theta$的梯度
线性函数的反向传播：

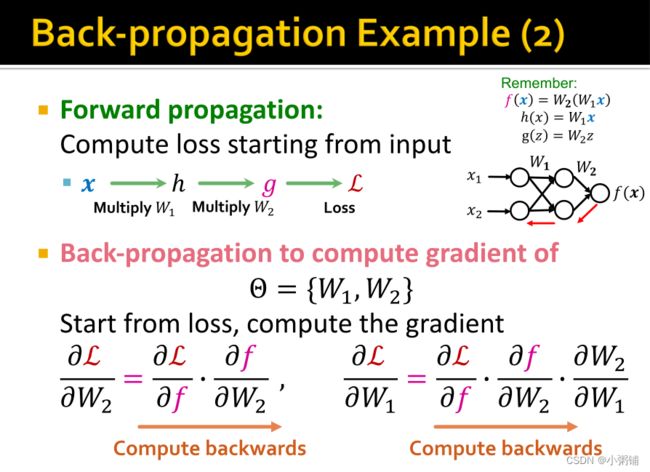
非线性函数的反向传播：

多层感知机（MLP）：

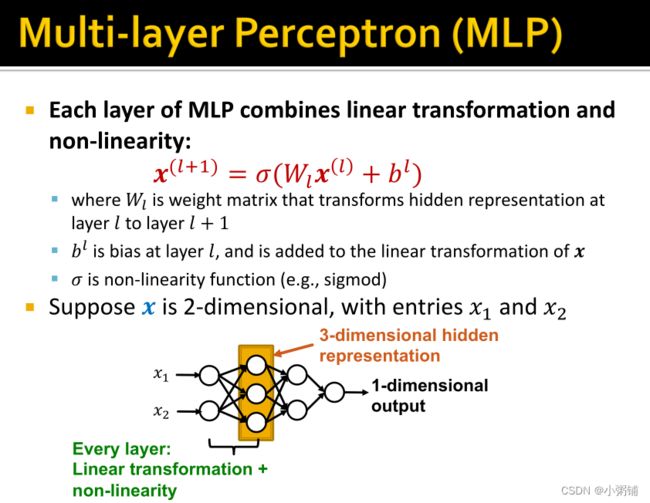
2.6 深度学习过程总结：

• 目标函数：
  $$mi{n}_{\Theta }L(y,f(x))$$
  目标函数f可以是一个简单的线性函数，一个多层感知机（MLP），或者其他神经网络（比如图神经网络）
• 我们对输入x采样小批量的数据
• 前向传播：对于给定输入x，计算损失L
• 后向传播：使用链式规则获得梯度${\nabla }_{w}L$
• 使用随机梯度下降法(SGD)在多次迭代中对参数$\Theta$进行优化

3. 图深度学习（Deep Learning for Graphs）

3.1 Setup

假设我们有一个图G：

• $V$：代表节点集
• $A$：代表邻接矩阵（只有0或1，未加权无向图）
• $v$和$N(v)$：v是节点集中的节点，N(v)是节点的邻域
• 节点特征：$X\in R^{m\times |V|}$是节点的特征矩阵
  • 社交网络中：节点特征是用户配置文件、用户图像
  • 生物网络中：节点特征是基因表达配置文件、基因功能信息
  • 当图形数据集中没有节点特征时，我们通常用下面两种方式表示：
    • 指示向量（节点的独热编码）
    • 值都为1的向量: [1, 1, …, 1]
    • 或者用节点度数作为节点特征

3.2 Deep Learning on Graph

一种简单地把神经网络用于图数据的方法：把图表示成邻接矩阵，再在邻接矩阵嵌入节点特征，最后把嵌入节点特征的邻接矩阵作为神经网络的输入。

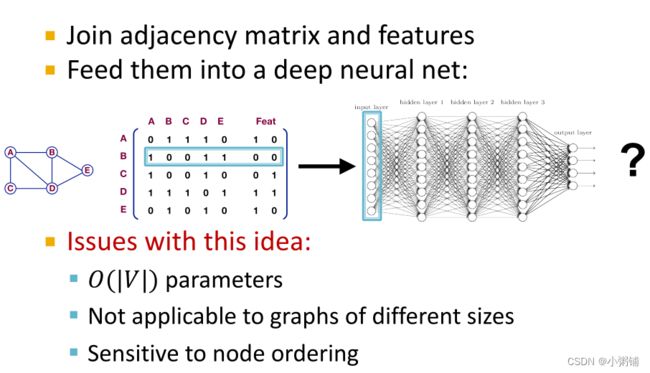
这种方法存在三个问题：

1. 参数数量与节点数成正比，需要$O(|V|)$个参数
2. 不适用于大小不同的图形
3. 对节点顺序敏感，节点顺序改变，邻接矩阵将会发生变化

解决方法：借鉴卷积网络的思想

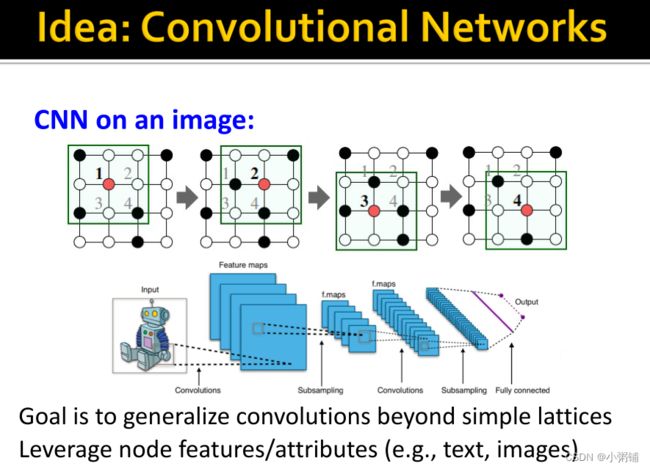
我们的想法是将目将卷积推广到简单格（如文本、图像）之外，同时利用节点特征/属性，但是图的结构会复杂得多：

图结构的问题：

• 图上没有固定的局部性或滑动窗口概念
• 图具有偏移不变性（即图没有节点的规范顺序，我们可以用不同方式定义节点顺序）
  • 这要求映射函数f应该将节点定义顺序不同但是结构完全相同的图映射到相同的图和节点表示
  • 其他神经网络，例如MLP等并不具有置换不变性，这就是我们第一种简单方法失败的原因。

那我们如何在图上定义滑动窗口呢？
通过传递和聚集来自邻居的信息，设计置换不变/相等的图形神经网络

4. Graph Convolutional Networks

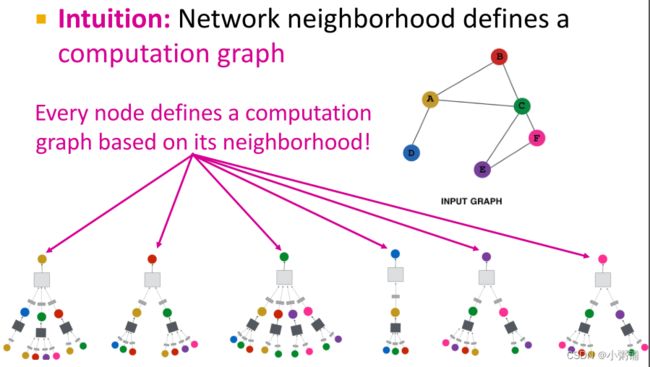
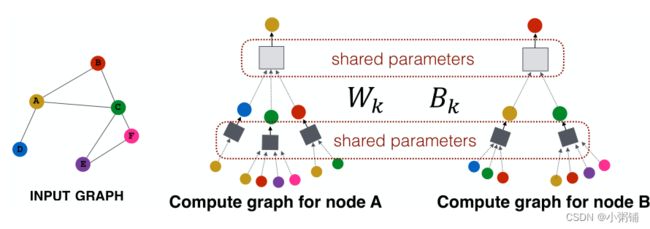
Idea: 节点的领域定义了一个计算图，我们要学习的是如何在图上传播并聚合信息以计算节点特征。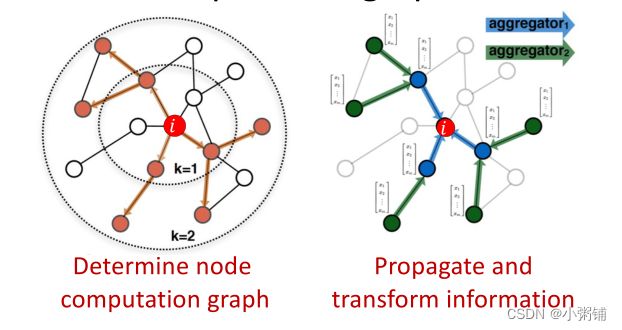
关键思想：基于本地网络邻域生成节点嵌入

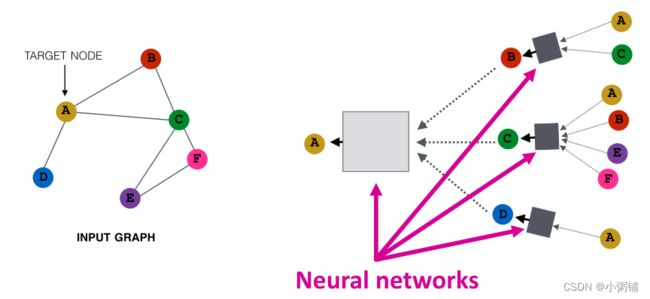
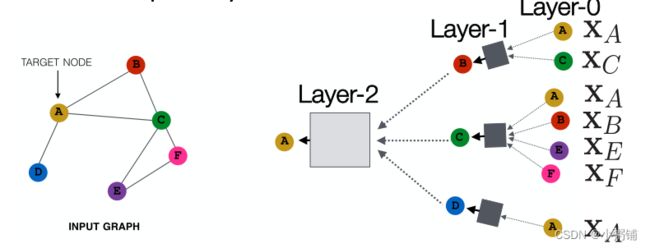
与经典神经网络的不同之处：图神经网络每个节点基于其邻域定义一个计算图，如果两个节点的网络邻域相似，那么这两个节点将具有相同的计算图。每个节点都有自己的神经网络架构，现在我们要同时训练或学习多种架构。

4.1 Graph Neural Networks Layers

• 模型可以具有任意深度
• 节点在每一层都有不同的嵌入
• 节点u的第0层嵌入是其输入特征$x_u$
• 第k层嵌入从距离K-hop的节点获取信息
  
  我们需要获取k跳的信息，就设计k层神经网络。

4.2 Neighborhood Aggregation

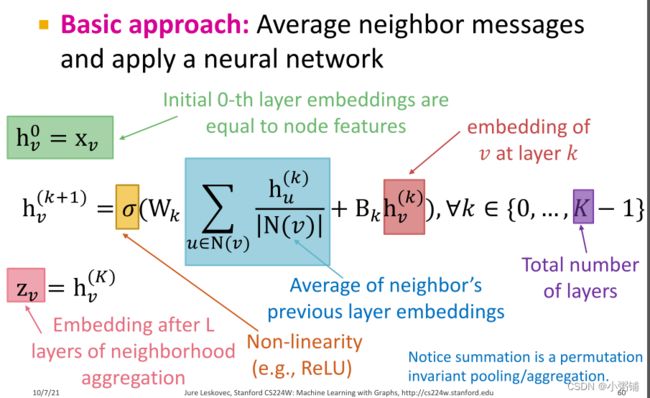
不同方法的关键区别在于它们是如何跨层聚合信息的（这里聚合算法也要满足排列不变性：无论节点顺序如何，聚合结果始终相同）。

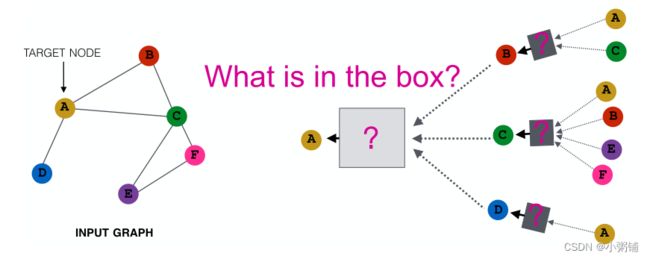
基本方法：对来自邻域的所有信息求平均值并应用于神经网络。

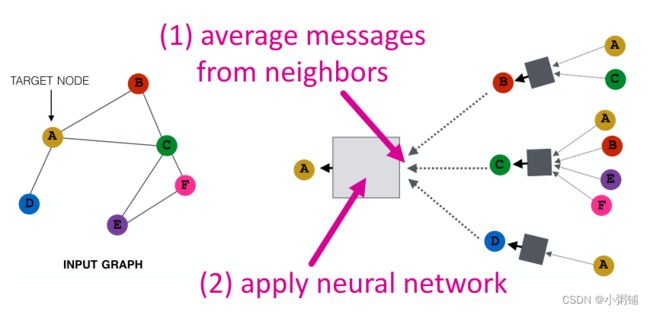
4.3 深度编码器

注意：图卷积网络中的消息传递和邻居聚合是置换等变的

4.4 模型训练

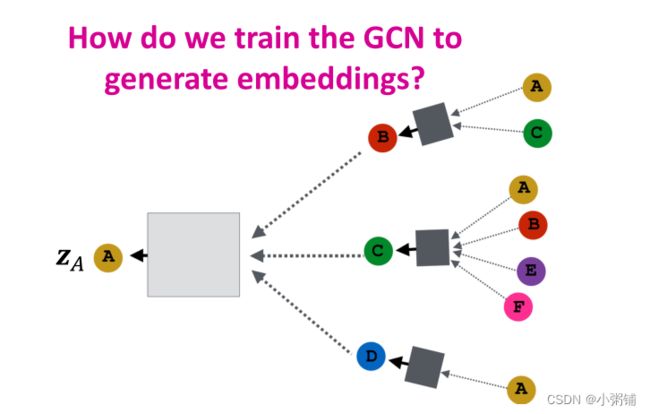
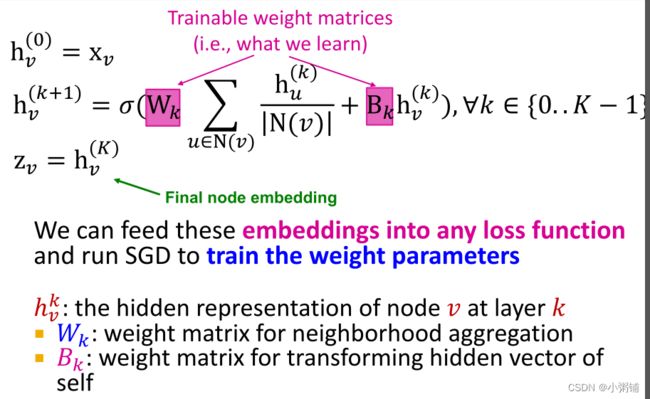
那我们应该如何训练模型生成嵌入呢？ 首先，我们需要在嵌入上定义一个损失函数。

可训练的模型参数：

注意：权重矩阵在节点之间共享。

我们将聚合算式写成矩阵的形式：许多聚合可以通过（稀疏）矩阵运算有效地执行：

• $H^{(k)}=[h_1^{(k)}...h_{|V|}^{(k)}{]}^T$
• 那么：${\sum }_{u\in N_v}{h}_u^{(k)}=A_v{H}^{(l)}$
• D是对角矩阵，其中
  $$D_{v,v}=Deg(v)=|N(v)|$$
  D的逆矩阵$D^{-1}$也是对角矩阵，$D_{v,v}^{-1}=1/|N(v)|$
• 因此，
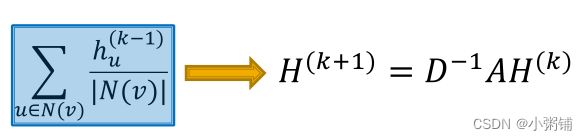
  更新函数可以写成以下的形式：
  
  实际上，这意味着可以使用有效的稀疏矩阵（$\tilde{A}$是稀疏的）乘法来更新节点嵌入，训练模型
  注意：当聚合函数复杂时，并非所有GNN都可以矩阵形式表示

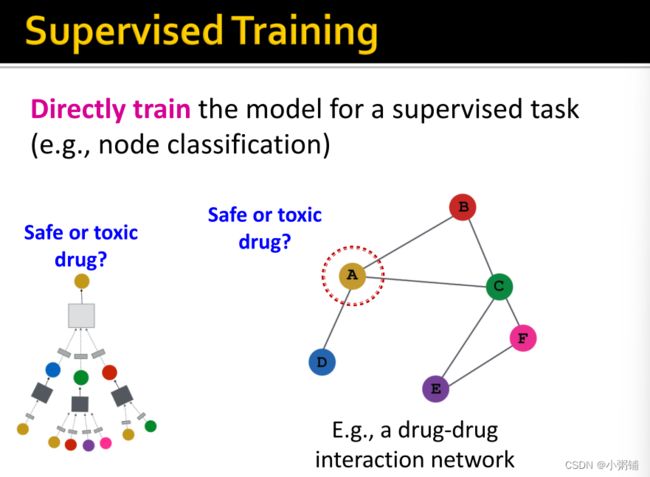
4.5 监督学习和无监督学习

无监督学习：

监督学习：

4.6 图神经网络现代设计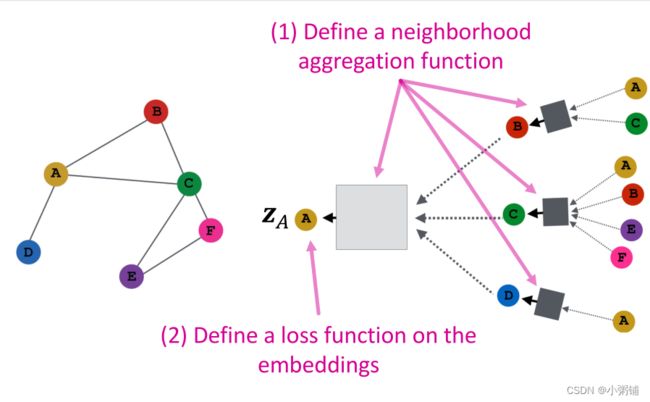

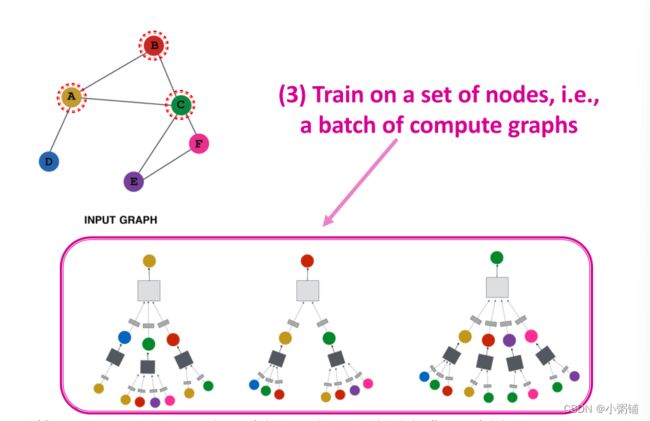
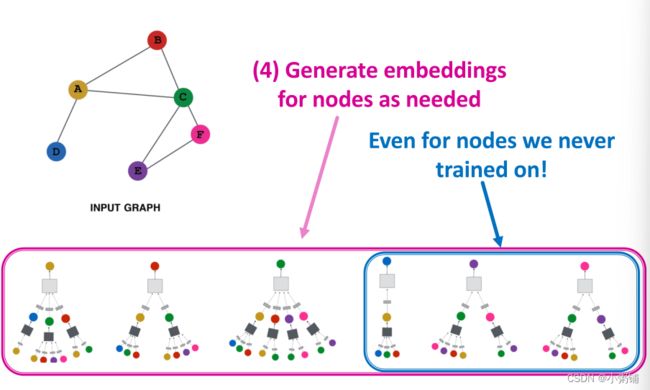
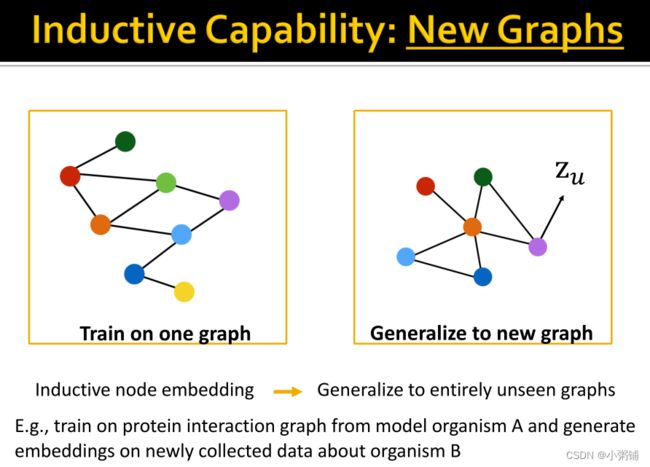
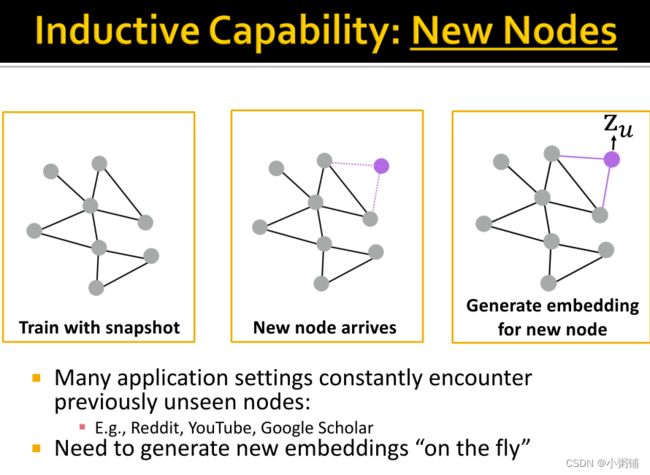
图神经网络模型经过训练后，可以为图中从未出现过的节点生成嵌入，说明该模型有归纳能力

• 所有节点共享相同的聚合参数
• 模型参数的数量与节点数|V|是次线性的，我们可以将其推广到看不见的节点
  
  
  

4. GNNs VS CNNs and Transformer

4.1 GNNs VS. CNN

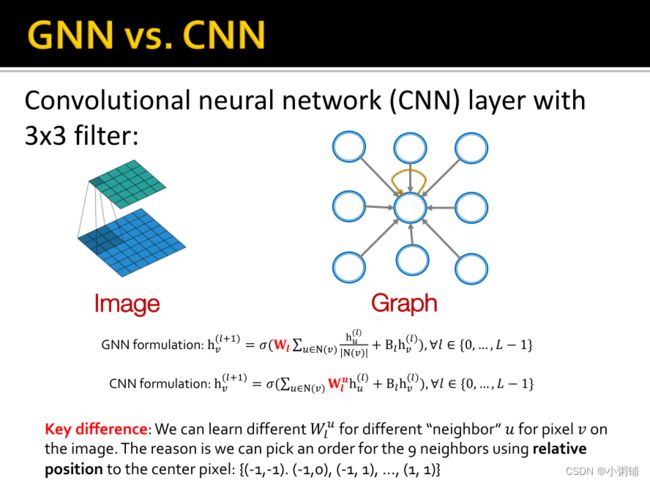
主要区别：在CNNs中，对于图像上的像素 v，我们可以为不同的“邻居”u 学习不同的权重$W_l^u$，因为我们可以使用与中心像素的相对位置为 9 个邻居选择顺序: {(-1, -1). (-1,0), (-1, 1), …, (1, 1)}

CNN 可以被视为邻居大小和排序固定的特殊 GNN：

• CNN中滤波器的大小是预定义的。
• GNN 的优点是它能处理每个节点的度数都不相同的任意图
• CNN并不具有置换不变性，改变像素位置会导致不同的输出

4.2 GNNs VS. Transformer

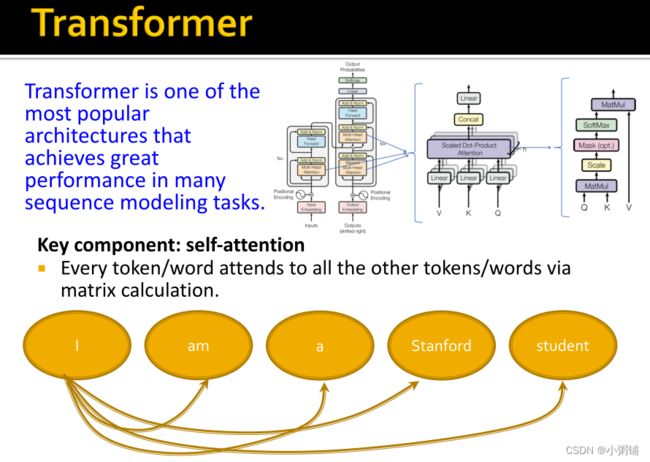
Transformer是最流行的架构之一，它在许多序列建模任务中实现了出色的性能。
关键组成部分：self-attention
每个标记/词都通过矩阵计算来关注所有其他标记/词。

Transformer模型的每一层可以被看作是一个特殊的GNN，在一个完全连接的 "word"图上运行。由于每个词都关注所有其他的词，所以转换层的计算图与全连接的 "词 "图上的GNN的计算图相同。

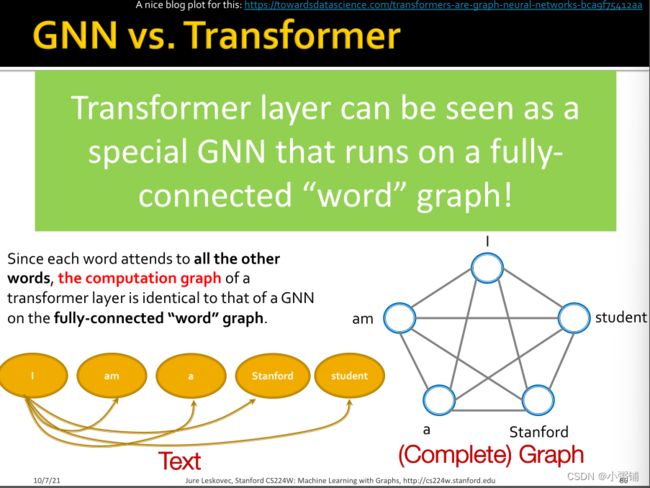
GNN是一个通用架构，CNN和Transformer可以被看作是一个特殊的GNN。