深度学习笔记——波士顿房价预测

初次接触深度学习，记录一点思考和想法，请大家多多指正。

首先是工具包的导入pycharm

这里我用到了numpy科学计算库，json轻量级的数据交换格式包，以及matplotlib绘图工具包

import numpy as np
import json
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

 首先我们的目的是用13个有关因素预测房价，相当于有13个自变量x，1个输出y，我们要寻找这些x，与y之间的函数。

首先是数据的预处理

我们有大概500多个数据，类似于这样的形式，它们之间用空格分开。

 使用np.fromdata来读取数据记录在data一维数组中，sep参数我猜测是这个函数读取数据的方式，如果有空格分开就代表这空格两边各有一个数据。之后将data由一维的数组用reshape函数转化为一个14*506的数组矩阵，再将其中的80%的数据用来训练，20%的数据用来测试。随后对数据进行归一化处理，归一化的目的为了将来取下降梯度计算的detla值更方便，这里我也不太明白是为什么。

def load_data():
    datafile='/home/xiaobin0264/fzb/datafile/housing.data'
    data=np.fromfile(datafile,sep=' ')
    #定义十三个变量名
    feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS',
                     'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
    feature_num = len(feature_names)
    data = data.reshape([data.shape[0] // feature_num, feature_num])
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]
    #求出训练数据的最大值最小值和平均值
    datamax,datamin,avgs=\
        training_data.max(axis=0),\
        training_data.min(axis=0),\
        training_data.sum(axis=0) / training_data.shape[0]
    for i in range(feature_num):
        print(datamin[i], datamin[i], avgs[i])
        data[:, i] = (data[:, i] - datamin[i]) / (datamax[i] - datamin[i])

    test_data = data[offset:]
    return training_data,test_data

training_data, test_data = load_data()
#x方向全选，y方向选到最后一组
x = training_data[:, :-1]
y = training_data[:, -1:]

将输入因素x，和输出房价y，分别从training_data训练数据中取出，建立一个神经网络的类Network将其中神经元权重的w，和b初始化，这里我用随机数初始化了13个w的权重，初始化偏置b为0

forwoard 函数为前向计算函数，作用是用来计算当前的权重和偏置下的预测值z

loss函数为损失函数，这里因为我们所预测的房价是一个连续的实数，因此我们使用均方差来计算预测值和实际值的损失，至于为什么用均方差不用绝对值差，是因为后面我们计算梯度下降时为了考虑到梯度的存在性，均方差会比绝对值差更好。

gradient 函数为梯度计算函数，我们为了使我们的loss函数最小，要找出一个w和一个b使loss处于最低点，但我们不知道何处是最低，所以我们先采用一个随机的w和b，通过计算函数梯度的梯度来判断此时我们的w和b处于一个怎样的趋势，若梯度为负值，我们增大自变量，函数值就会下降，反之则增大。所以为了求得最小值我们使用梯度下降的方法，通过不断地迭代计算，每次通过计算的梯度，对w和b进行反梯度的很小的移动。

update 函数为更新函数，对每次迭代后产生新的w，b进行更新，用来做下一次计算。

train 函数 训练函数，将上述所有的操作整合

class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)
        self.b = 0.

    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z

    def loss(self, z, y):
        error = z - y
        cost = error * error
        cost = np.mean(cost)
        return cost

    def gradient(self, x, y):
        z = self.forward(x)
        gradient_w = (z - y) * x
        gradient_w = np.mean(gradient_w, axis=0)
        #这里增加axis轴是为了使梯度矩阵由横向矩阵变为竖向矩阵便于后面加减计算
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = (z - y)
        gradient_b = np.mean(gradient_b)
        return gradient_w, gradient_b
    def update(self,gradient_w,gradient_b,delta=0.01):
        self.w=self.w-gradient_w*delta
        self.b=self.b-gradient_b*delta
    def train(self,x, y,iterations=100,delta=0.01):
        losses=[]
        for i in range(iterations):
            z=self.forward(x)
            L=self.loss(z,y)
            gradient_w,gradient_b=self.gradient(x,y)
            self.update(gradient_w,gradient_b)
            losses.append(L)
            if (i+1)%10==0:
                print("itera={},loss={}".format(i,L))
        return losses

以下是代码的实现调用，用matplotlib显示训练的loss变化过程

train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
num_iterations = 2000
# 启动训练
losses = net.train(x, y, iterations=num_iterations, delta=0.01)

# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
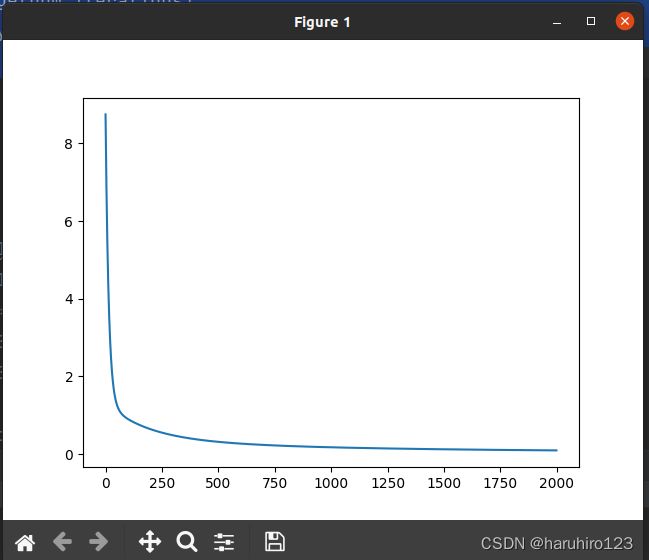
plt.plot(plot_x, plot_y)

结果是这样

y轴是losses损失，x轴是迭代次数