决策树的构造——进阶处理
由前一篇文章决策树的构造我们了解了什么是决策树,离散型数据的代码实现以及构造它的决策树图形,接下来我们继续了解关于决策树的算法类型ID3算法,C4.5算法,CART算法,以及数据的离散化处理和决策树的预剪枝和后剪枝操作。
决策树算法类型
ID3算法
ID3算法其实我们很熟悉,上篇文章的操作处理就是ID3算法的实现,通过计算每个特征值的信息增益来构造决策树,它较为简单,容易构建,但是它简单自然也有缺点,它并不支持连续值处理,缺失值处理和剪枝操作。因此为解决ID3算法中存在的这些缺陷,于是出现了在此基础上进行改进的C4.5算法和CART算法。
C4.5算法
C4.5算法作为数据挖掘领域的十大经典算法,它是以ID3算法为基础进行改进,弥补了ID3无法处理连续数据,缺失数据,不支持剪枝等方面的不足,同时通过采用信息增益率的方法来选择属性,可以选择到更加合理的属性。
增益率公式如下
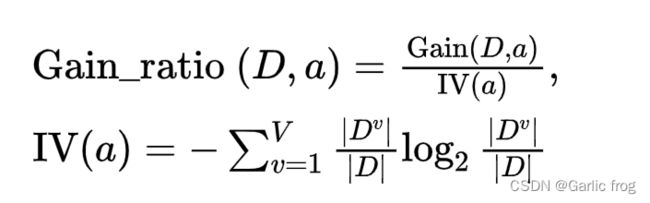
其中IV(a):称为属性a的固有值,属性a的可能取值越多,那么IV(a)通常越大。
例如,在上篇文章西瓜的例子中,IV(色泽)=1.580(V=3)
需要注意,增益率准则对取值数目较少的属性有所偏好,因此C4.5不直接选择增益率最大的候选划分属性,而是使用一个启发式,先从候选划分属性中找出信息增益高于平均水平的属性,然后再从中选择增益率最高的。
数据的离散化操作
将属性A的值进行升序排序,然后对其进行二分,计算每种划分方法的信息增益,选取信息增益最大的。
举例如下:
对上述属性进行二分,理论上有10-1=9中划分方法,不过我们在计算时只需要选择标签发生变化的地方进行划分,划分点选取为两属性的中间值,因此只有两种划分方法:
方法一:前4后6(年收入是否大于97)
方法二:前7后3(年收入是否大于80)
然后分别计算这两种划分方法的信息增益哪个信息增益大则使用那种方法划分。
CART算法
CART决策树(Classification and Regression Tree)使用基尼指数来选择划分属性,数据集的纯度用基尼值来度量:
基尼指数反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此基尼指数越小,数据集的纯度越高。
属性a的基尼指数定义如下: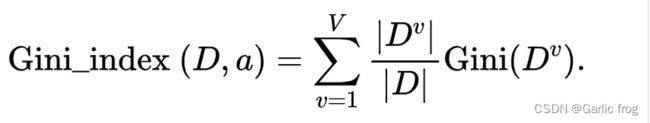
在候选属性集合a中,选择那个使得划分后基尼指数最小的属性作为最优划分属性。
预剪枝与后剪枝
为什么需要进行剪枝操作?
为了防止决策树模型的过拟合。
预剪枝:
在决策树生成的过程中,预先估计对结点进行划分能否提升决策树泛化性能。如果能提升,则对此结点进行划分,否则不划分。
优点:
1、使用预剪枝,决策树中很多分支未展开,可以很好的防止过拟合。
2、因为是在构造决策树的过程中进行的,所以时间开销比较小。
缺点:
1、预剪枝是基于贪心的策略。虽然一个结点进行划分不能带来泛化性能的提升,但很可能其后续结点能够带来泛化性能的提升。所以这种贪心策略放弃了一些泛化性能提升的可能性。
2、由于贪心策略,预剪枝决策树欠拟合的风险会比较大。
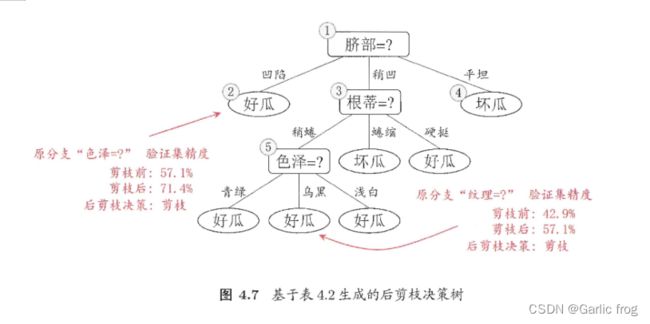
例子采用周志华同志的西瓜书例子
左右两张图可以很明显的看出左边是未进行预剪枝的决策树,右边是进行预剪枝操作后的决策树,我们计算其叶节点划分后的精度若测试结果大于划分前则进行划分若小于或相等则不进行划分。
后剪枝:
后剪枝是在决策树构建完成之后,自底向上地对每一个非叶结点进行考察,如果将此结点地子树替换为叶结点能够带来决策树模型泛化性能地提升,那么就将此非叶结点地子树替换为叶结点,否则不替换。
优点:
1、与预剪枝相比,保留了更多的分支,欠拟合风险比较小
2、泛化性能一般情况下也比预剪枝得到的决策树泛化性能好
缺点:
1、剪枝发生在决策树构建完成之后,而且要自底向上的检查每个非叶结点,时间开销会比较大。
左右两张图分别是未进行后剪枝和进行后剪枝后形成的决策树,与预剪枝一样的道理我们预测剪枝之后的精确度来判断我们是否进行剪枝操作。
实战代码实现
数据集使用西瓜书中的西瓜数据
| 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|
| 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 是 |
| 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
| 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 否 |
| 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 否 |
| 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 否 |
| 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
| 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
代码实现ID3
import math
import numpy as np
def createDataXG20():
data = np.array([['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
, ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑']
, ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
, ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑']
, ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
, ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘']
, ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘']
, ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑']
, ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑']
, ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘']
, ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑']
, ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘']
, ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑']
, ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑']
, ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘']
, ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑']
, ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑']])
label = np.array(['是', '是', '是', '是', '是', '是', '是', '是', '否', '否', '否', '否', '否', '否', '否', '否', '否'])
name = np.array(['色泽', '根蒂', '敲声', '纹理', '脐部', '触感'])
return data, label, name
def splitXgData20(xgData, xgLabel):
xgDataTrain = xgData[[0, 1, 2, 5, 6, 9, 13, 14, 15, 16],:]
xgDataTest = xgData[[3, 4, 7, 8, 10, 11, 12],:]
xgLabelTrain = xgLabel[[0, 1, 2, 5, 6, 9, 13, 14, 15, 16]]
xgLabelTest = xgLabel[[3, 4, 7, 8, 10, 11, 12]]
return xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest
# 定义一个常用函数 用来求numpy array中数值等于某值的元素数量
equalNums = lambda x,y: 0 if x is None else x[x==y].size
# 定义计算信息熵的函数
def singleEntropy(x):
"""计算一个输入序列的信息熵"""
# 转换为 numpy 矩阵
x = np.asarray(x)
# 取所有不同值
xValues = set(x)
# 计算熵值
entropy = 0
for xValue in xValues:
p = equalNums(x, xValue) / x.size
entropy -= p * math.log(p, 2)
return entropy
# 定义计算条件信息熵的函数
def conditionnalEntropy(feature, y):
"""计算 某特征feature 条件下y的信息熵"""
# 转换为numpy
feature = np.asarray(feature)
y = np.asarray(y)
# 取特征的不同值
featureValues = set(feature)
# 计算熵值
entropy = 0
for feat in featureValues:
# 解释:feature == feat 是得到取feature中所有元素值等于feat的元素的索引(类似这样理解)
# y[feature == feat] 是取y中 feature元素值等于feat的元素索引的 y的元素的子集
p = equalNums(feature, feat) / feature.size
entropy += p * singleEntropy(y[feature == feat])
return entropy
# 定义信息增益
def infoGain(feature, y):
return singleEntropy(y) - conditionnalEntropy(feature, y)
# 定义信息增益率
def infoGainRatio(feature, y):
return 0 if singleEntropy(feature) == 0 else infoGain(feature, y) / singleEntropy(feature)
# 特征选取
def bestFeature(data, labels, method = 'id3'):
assert method in ['id3', 'c45'], "method 须为id3或c45"
data = np.asarray(data)
labels = np.asarray(labels)
# 根据输入的method选取 评估特征的方法:id3 -> 信息增益; c45 -> 信息增益率
def calcEnt(feature, labels):
if method == 'id3':
return infoGain(feature, labels)
elif method == 'c45' :
return infoGainRatio(feature, labels)
# 特征数量 即 data 的列数量
featureNum = data.shape[1]
# 计算最佳特征
bestEnt = 0
bestFeat = -1
for feature in range(featureNum):
ent = calcEnt(data[:, feature], labels)
if ent >= bestEnt:
bestEnt = ent
bestFeat = feature
# print("feature " + str(feature + 1) + " ent: " + str(ent)+ "\t bestEnt: " + str(bestEnt))
return bestFeat, bestEnt
# 根据特征及特征值分割原数据集 删除data中的feature列,并根据feature列中的值分割 data和label
def splitFeatureData(data, labels, feature):
"""feature 为特征列的索引"""
# 取特征列
features = np.asarray(data)[:,feature]
# 数据集中删除特征列
data = np.delete(np.asarray(data), feature, axis = 1)
# 标签
labels = np.asarray(labels)
uniqFeatures = set(features)
dataSet = {}
labelSet = {}
for feat in uniqFeatures:
dataSet[feat] = data[features == feat]
labelSet[feat] = labels[features == feat]
return dataSet, labelSet
# 多数投票
def voteLabel(labels):
uniqLabels = list(set(labels))
labels = np.asarray(labels)
finalLabel = 0
labelNum = []
for label in uniqLabels:
# 统计每个标签值得数量
labelNum.append(equalNums(labels, label))
# 返回数量最大的标签
return uniqLabels[labelNum.index(max(labelNum))]
# 创建决策树
def createTree(data, labels, names, method = 'id3'):
data = np.asarray(data)
labels = np.asarray(labels)
names = np.asarray(names)
# 如果结果为单一结果
if len(set(labels)) == 1:
return labels[0]
# 如果没有待分类特征
elif data.size == 0:
return voteLabel(labels)
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(data, labels, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据选取的特征名称创建树节点
decisionTree = {bestFeatName: {}}
# 根据最优特征进行分割
dataSet, labelSet = splitFeatureData(data, labels, bestFeat)
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataSet.keys():
decisionTree[bestFeatName][featValue] = createTree(dataSet.get(featValue), labelSet.get(featValue), names, method)
return decisionTree
# 树信息统计 叶子节点数量 和 树深度
def getTreeSize(decisionTree):
nodeName = list(decisionTree.keys())[0]
nodeValue = decisionTree[nodeName]
leafNum = 0
treeDepth = 0
leafDepth = 0
for val in nodeValue.keys():
if type(nodeValue[val]) == dict:
leafNum += getTreeSize(nodeValue[val])[0]
leafDepth = 1 + getTreeSize(nodeValue[val])[1]
else :
leafNum += 1
leafDepth = 1
treeDepth = max(treeDepth, leafDepth)
return leafNum, treeDepth
# 使用模型对其他数据分类
def dtClassify(decisionTree, rowData, names):
names = list(names)
# 获取特征
feature = list(decisionTree.keys())[0]
# 决策树对于该特征的值的判断字段
featDict = decisionTree[feature]
# 获取特征的列
feat = names.index(feature)
# 获取数据该特征的值
featVal = rowData[feat]
# 根据特征值查找结果,如果结果是字典说明是子树,调用本函数递归
if featVal in featDict.keys():
if type(featDict[featVal]) == dict:
classLabel = dtClassify(featDict[featVal], rowData, names)
else:
classLabel = featDict[featVal]
return classLabel
# 可视化 主要源自《机器学习实战》
import matplotlib.pyplot as plt
decisionNodeStyle = dict(boxstyle = "sawtooth", fc = "0.8")
leafNodeStyle = {"boxstyle": "round4", "fc": "0.8"}
arrowArgs = {"arrowstyle": "<-"}
# 画节点
def plotNode(nodeText, centerPt, parentPt, nodeStyle):
createPlot.ax1.annotate(nodeText, xy = parentPt, xycoords = "axes fraction", xytext = centerPt
, textcoords = "axes fraction", va = "center", ha="center", bbox = nodeStyle, arrowprops = arrowArgs)
# 添加箭头上的标注文字
def plotMidText(centerPt, parentPt, lineText):
xMid = (centerPt[0] + parentPt[0]) / 2.0
yMid = (centerPt[1] + parentPt[1]) / 2.0
createPlot.ax1.text(xMid, yMid, lineText)
# 画树
def plotTree(decisionTree, parentPt, parentValue):
# 计算宽与高
leafNum, treeDepth = getTreeSize(decisionTree)
# 在 1 * 1 的范围内画图,因此分母为 1
# 每个叶节点之间的偏移量
plotTree.xOff = plotTree.figSize / (plotTree.totalLeaf - 1)
# 每一层的高度偏移量
plotTree.yOff = plotTree.figSize / plotTree.totalDepth
# 节点名称
nodeName = list(decisionTree.keys())[0]
# 根节点的起止点相同,可避免画线;如果是中间节点,则从当前叶节点的位置开始,
# 然后加上本次子树的宽度的一半,则为决策节点的横向位置
centerPt = (plotTree.x + (leafNum - 1) * plotTree.xOff / 2.0, plotTree.y)
# 画出该决策节点
plotNode(nodeName, centerPt, parentPt, decisionNodeStyle)
# 标记本节点对应父节点的属性值
plotMidText(centerPt, parentPt, parentValue)
# 取本节点的属性值
treeValue = decisionTree[nodeName]
# 下一层各节点的高度
plotTree.y = plotTree.y - plotTree.yOff
# 绘制下一层
for val in treeValue.keys():
# 如果属性值对应的是字典,说明是子树,进行递归调用; 否则则为叶子节点
if type(treeValue[val]) == dict:
plotTree(treeValue[val], centerPt, str(val))
else:
plotNode(treeValue[val], (plotTree.x, plotTree.y), centerPt, leafNodeStyle)
plotMidText((plotTree.x, plotTree.y), centerPt, str(val))
# 移到下一个叶子节点
plotTree.x = plotTree.x + plotTree.xOff
# 递归完成后返回上一层
plotTree.y = plotTree.y + plotTree.yOff
# 画出决策树
def createPlot(decisionTree):
fig = plt.figure(1, facecolor = "white")
fig.clf()
axprops = {"xticks": [], "yticks": []}
createPlot.ax1 = plt.subplot(111, frameon = False, **axprops)
# 定义画图的图形尺寸
plotTree.figSize = 1.5
# 初始化树的总大小
plotTree.totalLeaf, plotTree.totalDepth = getTreeSize(decisionTree)
# 叶子节点的初始位置x 和 根节点的初始层高度y
plotTree.x = 0
plotTree.y = plotTree.figSize
plotTree(decisionTree, (plotTree.figSize / 2.0, plotTree.y), "")
plt.show()
# 使用西瓜数据测试函数 p75-p77
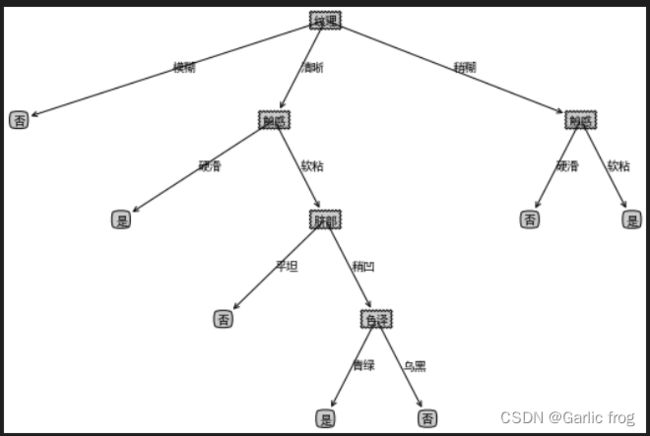
xgData, xgLabel, xgName = createDataXG20()
xgTree = createTree(xgData, xgLabel, xgName, method = 'id3')
print(xgTree)
createPlot(xgTree)
展示结果
预剪枝处理:
# 创建预剪枝决策树
def createTreePrePruning(dataTrain, labelTrain, dataTest, labelTest, names, method = 'id3'):
trainData = np.asarray(dataTrain)
labelTrain = np.asarray(labelTrain)
testData = np.asarray(dataTest)
labelTest = np.asarray(labelTest)
names = np.asarray(names)
# 如果结果为单一结果
if len(set(labelTrain)) == 1:
return labelTrain[0]
# 如果没有待分类特征
elif trainData.size == 0:
return voteLabel(labelTrain)
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(dataTrain, labelTrain, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据最优特征进行分割
dataTrainSet, labelTrainSet = splitFeatureData(dataTrain, labelTrain, bestFeat)
# 预剪枝评估
# 划分前的分类标签
labelTrainLabelPre = voteLabel(labelTrain)
labelTrainRatioPre = equalNums(labelTrain, labelTrainLabelPre) / labelTrain.size
# 划分后的精度计算
if dataTest is not None:
dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, bestFeat)
# 划分前的测试标签正确比例
labelTestRatioPre = equalNums(labelTest, labelTrainLabelPre) / labelTest.size
# 划分后 每个特征值的分类标签正确的数量
labelTrainEqNumPost = 0
for val in labelTrainSet.keys():
labelTrainEqNumPost += equalNums(labelTestSet.get(val), voteLabel(labelTrainSet.get(val))) + 0.0
# 划分后 正确的比例
labelTestRatioPost = labelTrainEqNumPost / labelTest.size
# 如果没有评估数据 但划分前的精度等于最小值0.5 则继续划分
if dataTest is None and labelTrainRatioPre == 0.5:
decisionTree = {bestFeatName: {}}
for featValue in dataTrainSet.keys():
decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
, None, None, names, method)
elif dataTest is None:
return labelTrainLabelPre
# 如果划分后的精度相比划分前的精度下降, 则直接作为叶子节点返回
elif labelTestRatioPost < labelTestRatioPre:
return labelTrainLabelPre
else :
# 根据选取的特征名称创建树节点
decisionTree = {bestFeatName: {}}
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataTrainSet.keys():
decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
, dataTestSet.get(featValue), labelTestSet.get(featValue)
, names, method)
return decisionTree
xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest = splitXgData20(xgData, xgLabel)
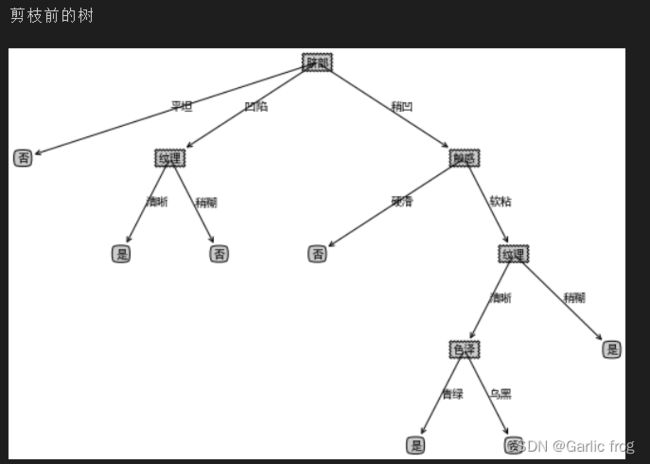
# 生成不剪枝的树
xgTreeTrain = createTree(xgDataTrain, xgLabelTrain, xgName, method = 'id3')
# 生成预剪枝的树
xgTreePrePruning = createTreePrePruning(xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest, xgName, method = 'id3')
print("剪枝前的树")
createPlot(xgTreeTrain)
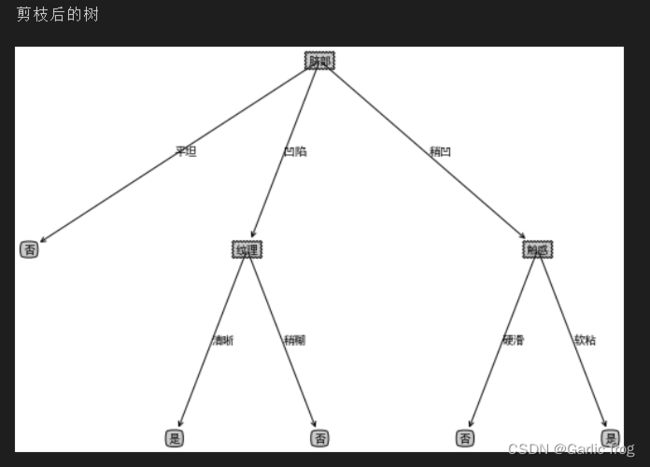
print("剪枝后的树")
createPlot(xgTreePrePruning)
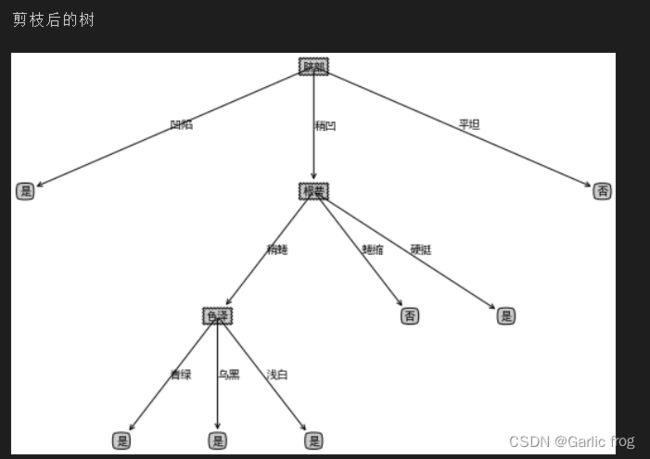
结果展示
后剪枝处理:
# 创建决策树 带预划分标签
def createTreeWithLabel(data, labels, names, method = 'id3'):
data = np.asarray(data)
labels = np.asarray(labels)
names = np.asarray(names)
# 如果不划分的标签为
votedLabel = voteLabel(labels)
# 如果结果为单一结果
if len(set(labels)) == 1:
return votedLabel
# 如果没有待分类特征
elif data.size == 0:
return votedLabel
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(data, labels, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据选取的特征名称创建树节点 划分前的标签votedPreDivisionLabel=_vpdl
decisionTree = {bestFeatName: {"_vpdl": votedLabel}}
# 根据最优特征进行分割
dataSet, labelSet = splitFeatureData(data, labels, bestFeat)
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataSet.keys():
decisionTree[bestFeatName][featValue] = createTreeWithLabel(dataSet.get(featValue), labelSet.get(featValue), names, method)
return decisionTree
def convertTree(labeledTree):
labeledTreeNew = labeledTree.copy()
nodeName = list(labeledTree.keys())[0]
labeledTreeNew[nodeName] = labeledTree[nodeName].copy()
for val in list(labeledTree[nodeName].keys()):
if val == "_vpdl":
labeledTreeNew[nodeName].pop(val)
elif type(labeledTree[nodeName][val]) == dict:
labeledTreeNew[nodeName][val] = convertTree(labeledTree[nodeName][val])
return labeledTreeNew
def treePostPruning(labeledTree, dataTest, labelTest, names):
newTree = labeledTree.copy()
dataTest = np.asarray(dataTest)
labelTest = np.asarray(labelTest)
names = np.asarray(names)
# 取决策节点的名称 即特征的名称
featName = list(labeledTree.keys())[0]
# print("\n当前节点:" + featName)
# 取特征的列
featCol = np.argwhere(names==featName)[0][0]
names = np.delete(names, [featCol])
# print("当前节点划分的数据维度:" + str(names))
# print("当前节点划分的数据:" )
# print(dataTest)
# print(labelTest)
# 该特征下所有值的字典
newTree[featName] = labeledTree[featName].copy()
featValueDict = newTree[featName]
featPreLabel = featValueDict.pop("_vpdl")
# print("当前节点预划分标签:" + featPreLabel)
# 是否为子树的标记
subTreeFlag = 0
# 分割测试数据 如果有数据 则进行测试或递归调用 np的array我不知道怎么判断是否None, 用is None是错的
dataFlag = 1 if sum(dataTest.shape) > 0 else 0
if dataFlag == 1:
# print("当前节点有划分数据!")
dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, featCol)
for featValue in featValueDict.keys():
# print("当前节点属性 {0} 的子节点:{1}".format(featValue ,str(featValueDict[featValue])))
if dataFlag == 1 and type(featValueDict[featValue]) == dict:
subTreeFlag = 1
# 如果是子树则递归
newTree[featName][featValue] = treePostPruning(featValueDict[featValue], dataTestSet.get(featValue), labelTestSet.get(featValue), names)
# 如果递归后为叶子 则后续进行评估
if type(featValueDict[featValue]) != dict:
subTreeFlag = 0
# 如果没有数据 则转换子树
if dataFlag == 0 and type(featValueDict[featValue]) == dict:
subTreeFlag = 1
# print("当前节点无划分数据!直接转换树:"+str(featValueDict[featValue]))
newTree[featName][featValue] = convertTree(featValueDict[featValue])
# print("转换结果:" + str(convertTree(featValueDict[featValue])))
# 如果全为叶子节点, 评估需要划分前的标签,这里思考两种方法,
# 一是,不改变原来的训练函数,评估时使用训练数据对划分前的节点标签重新打标
# 二是,改进训练函数,在训练的同时为每个节点增加划分前的标签,这样可以保证评估时只使用测试数据,避免再次使用大量的训练数据
# 这里考虑第二种方法 写新的函数 createTreeWithLabel,当然也可以修改createTree来添加参数实现
if subTreeFlag == 0:
ratioPreDivision = equalNums(labelTest, featPreLabel) / labelTest.size
equalNum = 0
for val in labelTestSet.keys():
equalNum += equalNums(labelTestSet[val], featValueDict[val])
ratioAfterDivision = equalNum / labelTest.size
# print("当前节点预划分标签的准确率:" + str(ratioPreDivision))
# print("当前节点划分后的准确率:" + str(ratioAfterDivision))
# 如果划分后的测试数据准确率低于划分前的,则划分无效,进行剪枝,即使节点等于预划分标签
# 注意这里取的是小于,如果有需要 也可以取 小于等于
if ratioAfterDivision < ratioPreDivision:
newTree = featPreLabel
return newTree
xgTreeBeforePostPruning = {"脐部": {"_vpdl": "是"
, '凹陷': {'色泽':{"_vpdl": "是", '青绿': '是', '乌黑': '是', '浅白': '否'}}
, '稍凹': {'根蒂':{"_vpdl": "是"
, '稍蜷': {'色泽': {"_vpdl": "是"
, '青绿': '是'
, '乌黑': {'纹理': {"_vpdl": "是"
, '稍糊': '是', '清晰': '否', '模糊': '是'}}
, '浅白': '是'}}
, '蜷缩': '否'
, '硬挺': '是'}}
, '平坦': '否'}}
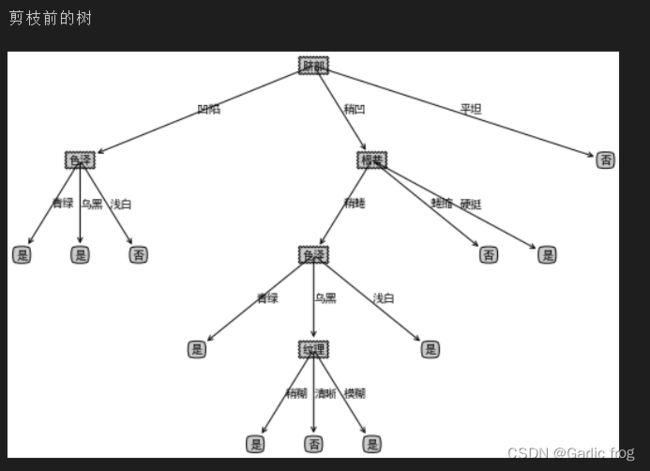
xgTreePostPruning = treePostPruning(xgTreeBeforePostPruning, xgDataTest, xgLabelTest, xgName)
print("剪枝前的树")
createPlot(convertTree(xgTreeBeforePostPruning))
print("剪枝后的树")
createPlot(xgTreePostPruning)
结果展示
代码参考:(38条消息) 决策树python源码实现(含预剪枝和后剪枝)_王路ylu的博客-CSDN博客_python决策树剪枝代码