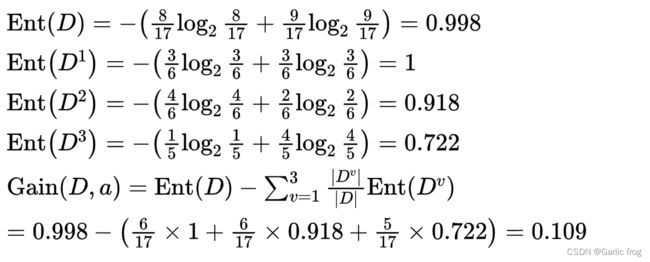决策树的构造

什么是决策树？

• 决策树( Decision Tree) 又称为判定树，是数据挖掘技术中的一-种重要的分类与回归方法，它是一种以树结构(包括二叉树和多叉树)形式来表达的预测分析模型。
• 决策树(Decision Tree) 是监督学习的一种算法。
• 决策树有两种:分类树和回归树。

信息熵和信息增益

熵定义为信息的期望值，所谓信息熵，我们不妨把它理解成某种特定信息的出现概率。
样本集合D中第k类样本所占的比例P_k（k=1,2,…,|Y|），|Y|为样本分类的个数，则D的信息熵为：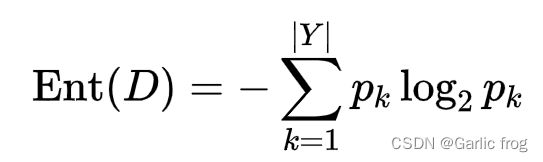

Ent(D)的值越小，则D的纯度越高。  

信息增益
使用属性a对样本集D进行划分所获得的“信息增益”的计算方法是，用样本集的总信息熵减去属性a的每个分支的信息熵与权重（该分支的样本数除以总样本数）的乘积，通常，信息增益越大，意味着用属性a进行划分所获得的“纯度提升”越大。因此，优先选择信息增益最大的属性来划分。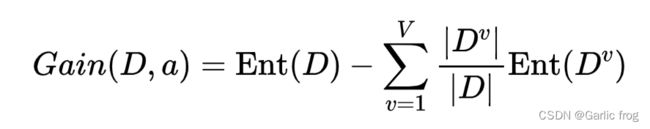

信息增益和构造决策树的关系

知道了如何计算信息增益，我们就可以计算每个特征值划分数据集获得的信息增益，获得的信息增益最高的特征值就是最好的选择，我们则可以将此特征值当作决策树的根节点，即按照特征值的信息增益的大小依次从上到下当作根节点。
举例如下：

色泽	根蒂	敲声	纹理	脐部	触感	好瓜
青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
青绿	蜷缩	沉闷	清晰	凹陷	硬滑	是
浅白	蜷缩	浊响	清晰	凹陷	硬滑	是
青绿	稍蜷	浊响	清晰	稍凹	软粘	是
乌黑	稍蜷	浊响	稍糊	稍凹	软粘	是
乌黑	稍蜷	浊响	清晰	稍凹	硬滑	是
乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	否
青绿	硬挺	清脆	清晰	平坦	软粘	否
浅白	硬挺	清脆	模糊	平坦	硬滑	否
浅白	蜷缩	浊响	模糊	平坦	软粘	否
青绿	稍蜷	浊响	稍糊	凹陷	硬滑	否
浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	否
乌黑	稍蜷	浊响	清晰	稍凹	软粘	否
浅白	蜷缩	浊响	模糊	平坦	硬滑	否
青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	否

 这边以色泽为例计算其信息增益，它有3个取值{青绿、乌黑、浅白}

Ent(D)为全部特征值的信息熵，总样本瓜数17个其中8个好瓜9个坏瓜。
Ent(D1)，Ent(D2)，Ent(D3)则分别为色泽青绿，乌黑，浅白的信息熵，青绿为例，则青绿总共6个瓜，其中3个好瓜3个坏瓜。
Gain(D，a)则为色泽这个特征值的信息增益，|D|则为总样本数，|Dv|则为每个色泽的样本数。

实例实现

数据处理

根据同学的学科的期末绩点及其课外成绩绩点计算其是否能得奖学金

序号	学科期末绩点	课外	是否能得奖学金
1	1	5	no
2	2	3	no
3	4	3	no
4	5	4	yes
5	4	5	yes
6	3	4	yes
7	1	4	no

代码实现：

导入所需库：

from math import log
import operator

计算给定数据集的熵：

from math import log
def calcShannonEnt(dataSet):
    numEntries = len(dataSet) 
    labelCounts = {}  # 字典dict
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1

    # 计算熵，以２为底求对数
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries  # 选择该分类的概率
        shannonEnt -= prob * log(prob, 2)  # 计算熵
    return shannonEnt

 按照给定特征划分数据集：

def splitDataSet(dataSet, axis, value):
    retDataSet = []  
    for featVec in dataSet:  
        if featVec[axis] == value:  
            reducedFeatVec = featVec[:axis] 
            reducedFeatVec.extend(featVec[axis+1:])  
            retDataSet.append(reducedFeatVec) 
    return retDataSet

 选择最好的数据集划分方式：

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1 
    baseEntropy = calcShannonEnt(dataSet)  
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]  
        uniqueVals = set(featList)  
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet) / float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

 采用多数表决的方法决定该叶子的节点分类：

def majorityCnt(classList):
    classCount = {}  # 数据字典
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1 
    sortedClassCount = sorted(classCount.iteritems(), key = operator.itemgetter(1), reversed = True)
    return sortedClassCount[0][0]

 创建树的函数代码：

def createTree(dataSet, labels):
    classList = [example[-1] for example in dataSet]  
    if classList.count(classList[0]) == len(classList):  
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)

    bestFeat = chooseBestFeatureToSplit(dataSet)  # 当前数据集选取的最好特征存储在bestFeat中
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}  # 字典变量存储了树所有的信息
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
    return myTree

导入数据集：

if __name__ == '__main__':

    dataSet = [[ '1', '5', 'no'],
              [ '2', '3','no'],
              [ '4', '3','no'],
              [ '5', '4', 'yes'],
              [ '4', '5', 'yes'],
              ['3', '4','yes'],
              ['1', '4','no']]
    labels = ['学科期末绩点','课外']
    myTree = createTree(dataSet, labels)

输出树结构： 

  print(myTree)

 绘制树形图：

获取叶节点的数目和树的层数：

def getNumLeafs(tree):
    numOfLeaf=0
    firstNode,=tree.keys()
    second=tree[firstNode]
    for key in second.keys():
        if type(second[key]).__name__=='dict':
            numOfLeaf+=getNumLeafs(second[key])
        else:
            numOfLeaf+=1
    return numOfLeaf
 
def getTreeDepth(tree):
    depthOfTree=0
    firstNode,=tree.keys()
    second=tree[firstNode]
    for key in second.keys():
        if type(second[key]).__name__=='dict':
            thisNodeDepth=getTreeDepth(second[key])+1
        else:
            thisNodeDepth=1
        if thisNodeDepth>depthOfTree:
            depthOfTree=thisNodeDepth
    return depthOfTree
 

 用matplotlib绘制决策树：

import matplotlib.pyplot as plt
decisionNode=dict(boxstyle='sawtooth',fc='0.8')       
leafNode=dict(boxstyle='round4',fc='1')     
arrow_args=dict(arrowstyle='<-')

def plotNode(nodeTxt,nodeIndex,parentNodeIndex,nodeType):  
    plt.annotate(nodeTxt,xy=parentNodeIndex,xycoords='axes fraction',
                            xytext=nodeIndex,textcoords='axes fraction',
                            va='center',ha='center',bbox=nodeType,
                            arrowprops=arrow_args)

def plotMidText(thisNodeIndex,parentNodeIndex,text):
    xmid=(parentNodeIndex[0]-thisNodeIndex[0])/2.0+thisNodeIndex[0]
    ymid=(parentNodeIndex[1]-thisNodeIndex[1])/2.0+thisNodeIndex[1]
    plt.text(xmid,ymid,text)                            

def plotTree(tree,parentNodeIndex,midTxt):
    global xOff
    global yOff
    numOfLeafs=getNumLeafs(tree)
    nodeTxt,=tree.keys()
    nodeIndex=(xOff+(1.0+float(numOfLeafs))/2.0/treeWidth,yOff)  #计算节点的位置
    plotNode(nodeTxt, nodeIndex, parentNodeIndex, decisionNode)
    plotMidText(nodeIndex,parentNodeIndex,midTxt)
    secondDict=tree[nodeTxt]
    yOff=yOff-1.0/treeDepth
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':
            plotTree(secondDict[key],nodeIndex,str(key))
        else:
            xOff=xOff+1.0/treeWidth
            plotNode(secondDict[key],(xOff,yOff),nodeIndex,leafNode)
            plotMidText((xOff,yOff),nodeIndex,str(key))
    yOff=yOff+1.0/treeDepth
 
def createPlot(tree):           
    fig=plt.figure('DecisionTree',facecolor='white')   
    fig.clf()                                          
    createPlot.ax1=plt.subplot(111,frameon=False)     
    global xOff
    xOff=-0.5/treeWidth
    global yOff
    yOff=1.0
    plotTree(tree,(0.5,1.0),'')
    plt.xticks([])
    plt.yticks([])
    plt.show()

def classify(inputTree,featureLabels,testVector):
    firstNode,=inputTree.keys()
    secondDict=inputTree[firstNode]
    featureIndex=featureLabels.index(firstNode)
    for key in secondDict.keys():
        if testVector[featureIndex]==key:
            if type(secondDict[key]).__name__=='dict':
                classLabel=classify(secondDict[key],featureLabels,testVector)
            else:
                classLabel=secondDict[key]
    return classLabel

def storeTree(inputTree,filename):
    import pickle
    file=open(filename,'wb')
    pickle.dump(inputTree,file)
    file.close()

def loadTree(filename):
    import pickle
    file=open(filename,'rb')
    Tree=pickle.load(file)
    file.close()
    return Tree

输入数据：

dataSet=[[1,5,'no'],[2,3,'no'],[4,3,'no'],[5,4,'yes'],[4,5,'yes'],[3,4,'yes'],[1,4,'no']]
labels=['学科期末绩点','课外']
decisionTree=createTree(dataSet,labels)
storeTree(decisionTree,'decisionTree')
myTree=loadTree('decisionTree')
featureLabels=['学科期末绩点','课外']
treeWidth=float(getNumLeafs(myTree))
treeDepth=float(getTreeDepth(myTree))
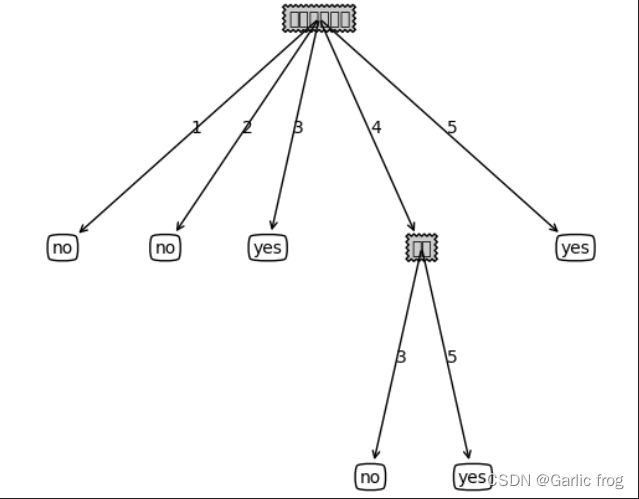
createPlot(myTree)

树的可视化结果：

测试决策树分类：

print(classify(myTree,featureLabels,[1,0]))
print(classify(myTree,featureLabels,[3,4]))

结果：

 测试结果符合预期。