决策树算法总结(上:ID3,C4.5决策树)
文章目录
- 一、决策树原理
-
- 1.1 决策树简介
- 1.2 基本概念
- 二、数学知识
-
- 2.1 信息熵
- 2.2 条件熵:
- 2.3 信息增益
- 三、ID3决策树
-
- 3.1 特征选择
- 3.2 算法思路
- 3.3 算法不足
- 四、C4.5决策树算法
-
- 4.1 处理连续特征
- 4.2 C4.5决策树特征选取
- 4.3 处理缺失值
- 4.4 过拟合问题
- 五、决策树C4.5算法的不足
决策树是一种特殊的树形结构,一般由节点和有向边组成。其中,节点表示特征、属性或者一个类。而有向边包含有判断条件。如图所示,决策树从根节点开始延伸,经过不同的判断条件后,到达不同的子节点。而上层子节点又可以作为父节点被进一步划分为下层子节点。一般情况下,我们从根节点输入数据,经过多次判断后,这些数据就会被分为不同的类别。这就构成了一颗简单的分类决策树。结点有两种类型:内部结点和叶节点。内部节点表示一个特征或属性, 叶节点表示一个类。
决策树(Decision Tree),又称为判定树,是一种以树结构(包括二叉树和多叉树)形式表达的预测分析模型。
一、决策树原理
1.1 决策树简介
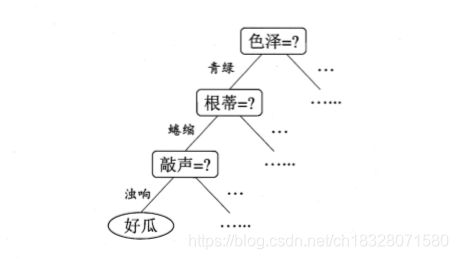
决策树是一种常见的机器学习方法。比如西瓜书中的例子,我们判断一个西瓜好坏,可以先判断色泽,然后在判断根蒂,再判断敲声,然后就可以得出好瓜和坏瓜,以此构建的树称为决策树。如下:
决策树属于非参数学习算法、可以用于解决(多)分类问题,回归问题。 回归问题的结果,叶子结点的平均值是回归问题的解。
- 分类树–对离散变量做决策树
- 回归树–对连续变量做决策树
本文只讲用于分类的决策树。
1.2 基本概念
- 根节点:决策树具有数据结构里面的二叉树、树的全部属性;
- 非叶子节点 :(决策点) 代表测试的条件,数据的属性的测试;
- 叶子节点 :分类后获得分类标记;
- 分支: 测试的结果。
用决策树分类:从根节点开始,对实例的某一特征进行测试,根据测试结果将实例分配到其子节点,此时每个子节点对应着该特征的一个取值,如此递归的对实例进行测试并分配,直到到达叶节点,最后将实例分到叶节点的类中。
- 决策树学习的目标:根据给定的训练数据集构建一个决策树模型,使它能够对实例进行正确的分类。
- 决策树学习的本质:从训练集中归纳出一组分类规则,或者说是由训练数据集估计条件概率模型。
- 决策树学习的损失函数:正则化的极大似然函数
- 决策树学习的测试:最小化损失函数
- 决策树学习的目标:在损失函数的意义下,选择最优决策树的问题。
- 决策树原理和问答猜测结果游戏相似,根据一系列数据,然后给出游戏的答案。
决策树的学习过程:
- 特征选择;
- 决策树生成: 递归结构, 对应于模型的局部最优;
- 决策树剪枝: 缩小树结构规模, 缓解过拟合, 对应于模型的全局选择。
二、数学知识
2.1 信息熵
“信息熵”information entropy是度量样本集合纯度最常用的一种指标,假定当前样本集合D中第k类样本所占比例为 p k p_k pk(k=1,2,…,|y|),则D的信息熵定义为:
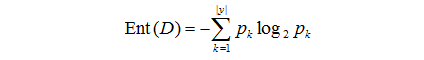
End(D)的值越小,则D的纯度越高。在信息论中,常用 H H H来表示信息熵。
举例说明:
比如说,明天会下雨吗?假设我们有历史上每天是否下雨的1000条记录,其中100天下雨,900天不下,那么我们这个系统的信息熵可以计算:
2.2 条件熵:
假设随机变量(X,Y), 其联合分布概率为 P ( X = x i , Y = y i ) = P i j , i = 1 , 2 , . . . , n ; j = 1 , 2 , . . , m P(X=x_i,Y=y_i)=P_{ij}, i=1,2,...,n;j=1,2,..,m P(X=xi,Y=yi)=Pij,i=1,2,...,n;j=1,2,..,m
则条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性, 其定义为X在给定条件下Y的条件概率分布的熵对X的数学期望:
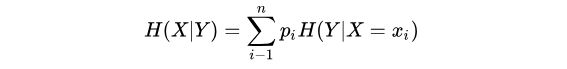
2.3 信息增益
信息增益是指某个信息条件下,系统整体的熵减少了多少,也就是整体信息熵减去条件信息熵的结果。用属性a对样本集D进行划分所获得的“信息增益”information gain:
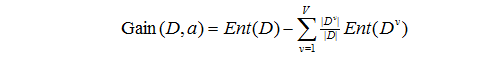
这里可能有些迷糊,下边构造决策树时,会有例题,跟着例题走,然后再回来看定义就比较清楚了。
三、ID3决策树
ID3决策树是原始的决策树,其依靠“信息增益“选择属性,称之为ID3决策树。当然,也有ID3、ID5决策树,下一章将讲解经典的C4.0决策树。
构造决策树主要由以下三部分:
- 特征选择;
- 决策树生成: 递归结构, 对应于模型的局部最优;
- 决策树剪枝: 缩小树结构规模, 缓解过拟合, 对应于模型的全局选择。
算法流程如下:

决策树的生成是一个递归过程,在决策树基本算法中,有三种情形会导致递归返回:
- (1)当前节点包含的样本全属于同一类别,无需划分;
- (2)当前属性集为空,或是所有样本在所有属性上取值相同,无法划分;把当前结点标记为叶结点,并将其类别设定为该结点所含样本最多的类别,利用了当前结点的后验分布;
- (3)当前结点包含的样本集合为空,不能划分,把当前结点标记为叶结点,但将其类别设定为其父节点所含样本最多的类别,这里是将父结点的样本分布作为当前结点的先验分布。
3.1 特征选择
上述算法中,对于属性 A = { a 1 , a 2 , . . . , a d } A=\{a_1,a_2,...,a_d\} A={ a