python线性回归实现波士顿房价预测(激活函数)
这里写自定义目录标题
- 激活函数
-
- 激活函数的作用
- 激活函数的分类
-
- Sigmoid
- Relu
- Tanh
- Leaky_relu
- 激活函数的应用
激活函数
激活函数的作用
生活中真实的例子很复杂,很难将所有的数据用直线来表示出来,实际上真实的数据更容易用曲线表示。所以引入了激活函数。
激活函数的分类
常用的激活函数有Sigmoid,relu,tanh,leaky_relu。
Sigmoid
S i g m o i d ( x ) = 1 1 + e − x Sigmoid(x)= \frac{1}{1+e^{-x}} Sigmoid(x)=1+e−x1
∂ S i g m o i d ( x ) ∂ x = S i g m o i d ( x ) ∗ ( 1 − S i g m o i d ( x ) ) \frac{\partial{Sigmoid(x)}}{\partial{}x}=Sigmoid(x)*(1-Sigmoid(x)) ∂x∂Sigmoid(x)=Sigmoid(x)∗(1−Sigmoid(x))
S i g m o i d ( x ) Sigmoid(x) Sigmoid(x)函数图像

∂ S i g m o i d ∂ x \frac{\partial{Sigmoid}}{\partial{}x} ∂x∂Sigmoid函数图像

Sigmoid的优点是:
- 能压缩数据,保证数据幅度不会有问题。
- 便于求导的平滑函数。
- 适合用于前向传播。
Sigmoid的缺点是:
- 容易出现梯度消失(gradient vanishing)的现象。
- Sigmoid 的 output 不是0均值,使得收敛缓慢。
- 幂运算相对耗时。
Relu
R e l u ( x ) = { x , x>=0 0 , x<0 Relu(x) = \begin{cases}x, & \text{x>=0} \\0, & \text{x<0} \end{cases} Relu(x)={x,0,x>=0x<0
∂ R e l u ( x ) ∂ x = { 1 , x>=0 0 , x<0 \frac{\partial{Relu(x)}}{\partial{x}}=\begin{cases}1, & \text{x>=0} \\0, & \text{x<0} \end{cases} ∂x∂Relu(x)={1,0,x>=0x<0
R e l u ( x ) Relu(x) Relu(x) 的函数图像

∂ R e l u ( x ) ∂ x \frac{\partial{Relu(x)}}{\partial{x}} ∂x∂Relu(x)函数图像
 R e l u ( x ) Relu(x) Relu(x)的优点是
R e l u ( x ) Relu(x) Relu(x)的优点是
- ReLu的收敛速度比 sigmoid 和 tanh 快。
- 适合用于后向传播。
R e l u ( x ) Relu(x) Relu(x)的缺点是
- Relu的 output 不是0均值,使得收敛缓慢。
- 某些神经元可能永远不会被激活,导致相应参数永远不会被更新。
- ReLU不会对数据做幅度压缩,所以数据的幅度会随着模型层数的增加不断扩张。
Tanh
T a n h ( x ) = e x − e − x e x + e − x Tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} Tanh(x)=ex+e−xex−e−x
∂ T a n h ( x ) ∂ x = 1 − ( T a n h ( x ) ) 2 \frac{\partial{Tanh(x)}}{\partial{x}}=1-(Tanh(x))^2 ∂x∂Tanh(x)=1−(Tanh(x))2
T a n h ( x ) Tanh(x) Tanh(x)函数图像

∂ T a n h ( x ) ∂ x \frac{\partial{Tanh(x)}}{\partial{x}} ∂x∂Tanh(x)函数图像

T a n h ( x ) Tanh(x) Tanh(x)的优点是
- Tanh函数是0均值的更加有利于提高训练效率
T a n h ( x ) Tanh(x) Tanh(x)的缺点是
- 梯度消失(gradient vanishing)的问题和幂运算的问题仍然存在。
Leaky_relu
L e a k y _ r e l u ( x ) = { x , x>=0 α ∗ x , x<0 Leaky\_relu(x) = \begin{cases}x, & \text{x>=0} \\ \alpha*x, & \text{x<0} \end{cases} Leaky_relu(x)={x,α∗x,x>=0x<0
∂ L e a k y _ r e l u ( x ) ∂ x = { 1 , x>=0 α , x<0 \frac{\partial{Leaky\_relu(x)}}{\partial{x}}=\begin{cases}1, & \text{x>=0} \\ \alpha, & \text{x<0} \end{cases} ∂x∂Leaky_relu(x)={1,α,x>=0x<0
L e a k y _ r e l u ( x ) Leaky\_relu(x) Leaky_relu(x)函数图像
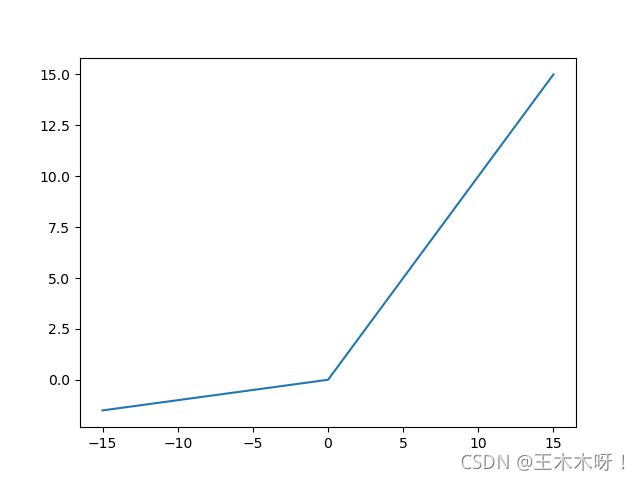
∂ L e a k y _ r e l u ( x ) ∂ x \frac{\partial{Leaky\_relu(x)}}{\partial{x}} ∂x∂Leaky_relu(x)函数图像
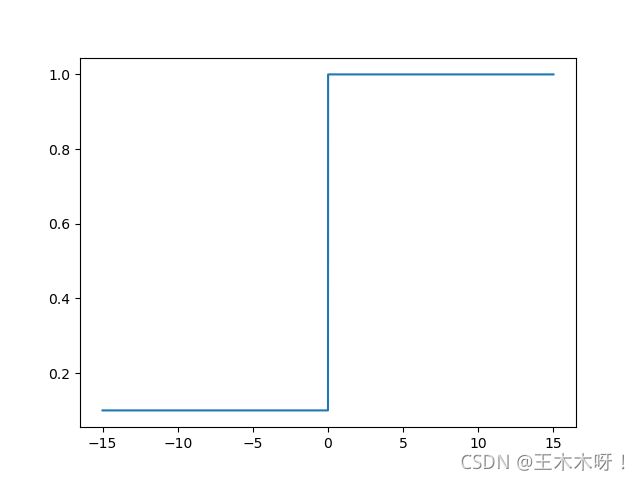
L e a k y _ r e l u Leaky\_relu Leaky_relu的优点是
- 解决了Relu的神经元死亡问题问,在负区域具有小的正斜率,因此即使对于负输入值,它也可以进行反向传播。
- 具有Relu函数的优点。
L e a k y _ r e l u Leaky\_relu Leaky_relu的缺点是
- 结果不一致,无法为正负输入值提供一致的关系预测(不同区间函数不同)。
激活函数的应用
我们依然使用波士顿房价预测这个例子,将原来的 y = k x + b y=kx+b y=kx+b改为
f ( x ) = k 2 ∗ S i g m o i d ( k 1 ∗ x + b 1 ) + b 2 f(x)=k_2*Sigmoid(k_1*x+b_1)+b_2 f(x)=k2∗Sigmoid(k1∗x+b1)+b2
损失函数依然使用 L o s s = ∑ y t r u e − y h a t n Loss=\frac{\sum{y_{true}-y_{hat}}}{n} Loss=n∑ytrue−yhat
对 b 2 b_2 b2求偏导得
∂ L o s s ∂ b 2 = − 2 ∗ ∑ y t r u e − y h a t n \frac{\partial Loss}{\partial b_2}=-2*\frac{\sum{y_{true}-y_{hat}}}{n} ∂b2∂Loss=−2∗n∑ytrue−yhat
对 k 2 k_2 k2求偏导得
∂ L o s s ∂ k 2 = − 2 ∗ ∑ ( y t r u e − y h a t ) ∗ S i g m o i d ( k 1 ∗ x + b 1 ) n \frac{\partial Loss}{\partial k_2}=-2*\frac{\sum{(y_{true}-y_{hat})*Sigmoid(k_1*x + b_1)}}{n} ∂k2∂Loss=−2∗n∑(ytrue−yhat)∗Sigmoid(k1∗x+b1)
对 b 1 b_1 b1求偏导得
∂ L o s s ∂ b 1 = − 2 ∗ ∑ ( y t r u e − y h a t ) ∗ k 2 ∗ S i g m o i d ( k 1 ∗ x + b 1 ) ∗ ( 1 − S i g m o i d ( k 1 ∗ x + b 1 ) ) n \frac{\partial Loss}{\partial b_1}=-2*\frac{\sum{(y_{true}-y_{hat})*k_2*Sigmoid(k_1*x + b_1)*(1-Sigmoid(k_1*x + b_1))}}{n} ∂b1∂Loss=−2∗n∑(ytrue−yhat)∗k2∗Sigmoid(k1∗x+b1)∗(1−Sigmoid(k1∗x+b1))
对 k 1 k_1 k1求偏导得
∂ L o s s ∂ k 1 = − 2 ∗ ∑ x ∗ ( y t r u e − y h a t ) ∗ k 2 ∗ S i g m o i d ( k 1 ∗ x + b 1 ) ∗ ( 1 − S i g m o i d ( k 1 ∗ x + b 1 ) ) n \frac{\partial Loss}{\partial k_1}=-2*\frac{\sum{x*(y_{true}-y_{hat})*k_2*Sigmoid(k_1*x + b_1)*(1-Sigmoid(k_1*x + b_1))}}{n} ∂k1∂Loss=−2∗n∑x∗(ytrue−yhat)∗k2∗Sigmoid(k1∗x+b1)∗(1−Sigmoid(k1∗x+b1))
求偏导得函数依次为:
# 对b2求偏导
def partial_b2(y_ture, y_hat):
return -2 * np.mean(np.array(y_ture)-np.array(y_hat))
# 对k2求偏导
def partial_k2(y_ture, y_hat, k1, b1, x):
s = 0
n = 0
for y_ture_i, y_hat_i, x_i in zip(y_ture, y_hat, x):
s += sigmoid(k1 * x_i + b1) * (y_ture_i - y_hat_i) * 2
n = n + 1
return -s/n
# 对b1求偏导
def partial_b1(y_ture, y_hat, k1, b1, x):
s = 0
n = 0
for y_ture_i, y_hat_i, x_i in zip(y_ture, y_hat, x):
s += 2 * (y_ture_i - y_hat_i) * k2 * (sigmoid(k1 * x_i + b1) - sigmoid(k1 * x_i + b1) ** 2)
n = n + 1
return (-1.0 * s)/(1.0 * n)
# 对k1求偏导
def partial_k1(y_ture, y_hat, k1, b1, x):
s = 0
n = 0
for y_ture_i, y_hat_i, x_i in zip(y_ture, y_hat, x):
s += 2 * x_i * (y_ture_i - y_hat_i) * k2 * (sigmoid(k1 * x_i + b1) - sigmoid(k1 * x_i + b1) ** 2)
n = n + 1
return (-1.0 * s)/(1.0 * n)
剩下学习步骤与训练 y = k ∗ x + b y=k*x+b y=k∗x+b同理
完整代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
data = load_boston()
X, Y = data['data'], data['target']
room_index = 5
X_rm = X[:, room_index]
def sigmoid(x):
return 1 / (1 + np.exp(-x))
k1, b1 = np.random.normal(), np.random.normal()
k2, b2 = np.random.normal(), np.random.normal()
print(k1,b1,k2,b2)
def model1(x, k1, b1):
return k1 * x + b1
def model2(x, k2, b2):
return k2 * x + b2
def y_hat(k1, k2, b1, b2, x):
Y1 = []
for i in x:
y1 = model1(i, k1, b1)
#print(y1)
y2 = sigmoid(y1)
#print(y2)
y3 = model2(y2, k2, b2)
Y1.append(y3)
return Y1
Y2 = y_hat(k1, k2, b1, b2, X_rm)
plt.scatter(X_rm, Y,color = 'red')
plt.scatter(X_rm,y_hat(k1, k2, b1, b2, X_rm))
plt.show()
# L2-Loss函数
def Loss(y_ture, y_hat):
return np.mean((np.array(y_ture) - np.array(y_hat)) ** 2)
# 对b2求偏导
def partial_b2(y_ture, y_hat):
return -2 * np.mean(np.array(y_ture)-np.array(y_hat))
# 对k2求偏导
def partial_k2(y_ture, y_hat, k1, b1, x):
s = 0
n = 0
for y_ture_i, y_hat_i, x_i in zip(y_ture, y_hat, x):
s += sigmoid(k1 * x_i + b1) * (y_ture_i - y_hat_i) * 2
n = n + 1
return -s/n
# 对k1求偏导
def partial_k1(y_ture, y_hat, k1, b1, x):
s = 0
n = 0
for y_ture_i, y_hat_i, x_i in zip(y_ture, y_hat, x):
s += 2 * x_i * (y_ture_i - y_hat_i) * k2 * (sigmoid(k1 * x_i + b1) - sigmoid(k1 * x_i + b1) ** 2)
n = n + 1
return (-1.0 * s)/(1.0 * n)
# 对b1求偏导
def partial_b1(y_ture, y_hat, k1, b1, x):
s = 0
n = 0
for y_ture_i, y_hat_i, x_i in zip(y_ture, y_hat, x):
s += 2 * (y_ture_i - y_hat_i) * k2 * (sigmoid(k1 * x_i + b1) - sigmoid(k1 * x_i + b1) ** 2)
n = n + 1
return (-1.0 * s)/(1.0 * n)
trying_time = 20000
min_loss = float('inf')
best_k1, best_b1 = None, None
best_k2, best_b2 = None, None
learning_rate = 1e-3
y_guess = y_hat(k1, k2, b1, b2, X_rm)
for i in range(trying_time):
# 将当前损失于最小损失相比较
y_guess = y_hat(k1, k2, b1, b2, X_rm)
loss = Loss(Y, y_guess)
if loss < min_loss:
best_k1 = k1
best_b1 = b1
best_k2 = k2
best_b2 = b2
min_loss = loss
if i % 1000 == 0:
print(min_loss)
# 找更合适的k与b
k1 = k1 - partial_k1(Y, y_guess, k1, b1, X_rm) * learning_rate
b1 = b1 - partial_b1(Y, y_guess, k1, b1, X_rm) * learning_rate
k2 = k2 - partial_k2(Y, y_guess, k1, b1, X_rm) * learning_rate
b2 = b2 - partial_b2(Y, y_guess) * learning_rate
plt.scatter(X_rm, Y,color = 'red')
plt.scatter(X_rm, y_hat(best_k1, best_k2, best_b1, best_b2, X_rm), color='green')
print('表示的函数为{} * sigmoid({} * x+ {} ) + {}'.format(best_k2,best_k1,best_b1,best_b2))
print('损失为{}'.format(min_loss))
plt.show()