特征工程
一、特征工程简介
二、特征构建
三、数据预处理
四、特征选择
五、特征提取
一、特征工程简介
1.1特征工程是什么?
特征工程是这样一个过程:将数据转换为能更好地表示潜在问题的特征,从而提高机器学习性能。
特征工程就是一个把原始数据转变成特征的过程,这些特征可以很好的描述这些数据,并且利用它们建立的模型在未知数据上的表现性能可以达到最优(或者接近最佳性能)。
从数学的角度来看,特征工程就是人工地去设计输入变量X。
1.2特征工程的重要性
特征越好,灵活性越强。好的特征的灵活性在于它允许你选择不复杂的模型,同时运行速度也更快,也更容易和维护。
特征越好,构建的模型越简单。好的特征可以在参数不是最优的情况,依然得到很好的性能,减少调参的工作量和时间,也就可以大大降低模型复杂度。
特征越好,模型的性能越出色。特征工程的目的本来就是为了提升模型的性能。
1.3特征工程的构成
特征工程是一个超集,一般认为包括特征构建、特征提取、特征选择三个部分。
二、特征构建
特征构建是指从原始数据中人工的构建新的特征。
特征构建需要很强的洞察力和分析能力,要求我们能够从原始数据中找出一些具有物理意义的特征。假设原始数据是表格数据,一般你可以使用组合属性来创建新的特征,或是分解原有的特征来创建新的特征。
介绍寻找高级特征最常用的方法有:
若干项特征加和: 我们假设你希望根据每日销售额得到一周销售额的特征。你可以将最近的7天的销售额相加得到。
若干项特征之差: 假设你已经拥有每周销售额以及每月销售额两项特征,可以求一周前一月内的销售额。
若干项特征乘积: 假设你有商品价格和商品销量的特征,那么就可以得到销售额的特征。
若干项特征除商: 假设你有每个用户的销售额和购买的商品件数,那么就是得到该用户平均每件商品的销售额。
小结:特征构建比较麻烦,需要一定的经验,需要结合具体的业务,花费大量的时间去观察原始数据,思考问题的潜在形式和数据结构,以及如何将特征数据输入给预测算法。
三、数据预处理
1、缺失值
处理缺失值的常用方法:
1)直接使用含有缺失值的特征:当仅有少量样本缺失该特征的时候可以尝试使用;
2)删除含有缺失值的特征:这个方法一般适用于大多数样本都缺少该特征,且仅包含少量有效值是有效的;
3)插值补全缺失值(均值/中位数/众数补全、固定值补全)
4)最近邻补全:寻找与该样本最接近的样本,使用其该属性数值来补全。
5)手动补全:根据对所在领域的理解,手动对缺失值进行插补的效果会更好。
6) 高维映射:将属性映射到高维空间,采用独热码编码(one-hot)技术。将包含 K 个离散取值范围的属性值扩展为 K+1 个属性值,若该属性值缺失,则扩展后的第 K+1 个属性值置为1。
2、异常值处理
常用的方法有两种:
1)聚类,比如我们可以用KMeans聚类将训练样本分成若干个簇,如果某一个簇里的样本数很少,而且簇质心和其他所有的簇都很远,那么这个簇里面的样本极有可能是异常特征样本了。我们可以将其从训练集过滤掉。
2)异常点检测方法,主要是使用iForest或者one class SVM,使用异常点检测的机器学习算法来过滤所有的异常点。
注意:某些筛选出来的异常样本是否真的是不需要的异常特征样本,最好找懂业务的再确认一下,防止我们将正常的样本过滤掉了。
3、日期/时间型变量
1)转为二值型,例如判断时间是否为一个节日、是否是周末、是否是高峰期等
2)转为离散型,例如将一天分为24小时、或者上午下午晚上
3)基于某个基准日期,转化为距离这一天的天数
4)与其他特征组合,例如前半个小时某个事件发生了多少次
4、数据离散化
在建模中,需要对连续变量离散化。特征离散化后,模型会更稳定,降低了模型过拟合的风险。
1)等距划分
从最小值到最大值之间,均分为 N 等份, 这样, 如果 A,B 为最小最大值, 则每个区间的长度为 W=(B−A)/N,则区间边界值为A+W,A+2W,….A+(N−1)W。这里只考虑边界,每个等份里面的实例数量可能不等。
2)等频划分
区间的边界值要经过选择,使得每个区间包含大致相等的实例数量。比如说 N=10 ,每个区间应该包含大约10%的实例。
3)自动规则划分
5、对类别型变量编码
1)哑编码
将定性数据编码为定量数据
作用是将不能够定量处理的变量量化,同时方便模型丢掉一些没用的特征。
2)one-hot编码
作用:
将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点。
几个特征合并到一个特征,达到降维的目的。
6、归一化/标准化
1)归一化
基于参数的模型或基于距离的模型,都要进行特征的归一化。
1.把数据变为[0,1]之间的小数。主要是为了方便数据处理,因为将数据映射到[0,1]范围之内,可以使处理过程更加便捷、快速。
2.把有量纲表达式变换为无量纲表达式,成为纯量。经过归一化处理的数据,处于同一数量级,可以消除指标之间的量纲和量纲单位的影响,提高不同数据指标之间的可比性。
主要算法:
1.线性转换,即min-max归一化(常用方法)
y=(x-min)/(max-min)
2. 对数函数转换
y=log10(x)
3.反余切函数转换
y=atan(x)*2/PI
2)标准化
数据的标准化是将数据按比例缩放,使之落入一个小的特定区间。
适用于数据的最大值和最小值未知,或存在孤立点。
主要算法:
1.z-score标准化,即零-均值标准化(常用方法)
y=(x-μ)/σ
将数据变换为均值为0、标准差为1的标准正态分布。
2.对数Logistic模式
y=1/(1+e^(-x))
7、处理不平衡数据
一般是两种方法:权重法或者采样法。
权重法
设置class weight和 sample weight
class weight对训练集里的每个类别加一个权重class weight。如果该类别的样本数多,那么它的权重就低,反之则权重就高。
sample weight对每个样本加权重,思路和类别权重也是一样,即样本数多的类别样本权重低,反之样本权重高。
sklearn中,绝大多数分类算法都有class weight和 sample weight可以使用。如果权重法做了以后发现预测效果还不好,可以考虑采样法。
2)采样法
对类别样本数多的样本做子采样
对类别样本数少的样本做过采样
(随机采样、SMOTE采样)
四、特征选择
特征选择是剔除不相关或者冗余的特征的过程,从而达到减少有效特征的个数,减少模型训练的时间,提高模型的精确度的效果。
特征选择,就是从多个特征中,挑选出一些对结果预测最有用的特征
特征选择主要有两个功能
1、减少特征数量、降维,使模型泛化能力更强
2、减少过拟合,增强对特征和特征值之间的理解
特征选择方法有很多,一般分为三类:
1)过滤法
方法: 评估单个特征和结果值之间的相关程度, 排序留下Top相关的特征部分。
按照特征的发散性或者相关性指标对各个特征进行评分,设定评分阈值或者待选择阈值的个数,选择合适特征。
代表:Chi-squared test (卡方检验)、 information gain (信息增益)、 correlation coefficient scores(相关系数)
缺点:只评估了单个特征对结果的影响,没有考虑到特征之间的关联作用,可能把有用的关联特征误踢掉。因此工业界使用比较少。
python包:SelectKBest指定过滤个数、SelectPercentile指定过滤百分比。
2)包裹型
方法:把特征选择看做一个特征子集搜索问题, 筛选各种特征子集,用模型评估效果。
根据目标函数,通常是预测效果评分,每次选择部分特征,或者排除部分特征。
代表: recursive feature elimination algorithm (递归特征消除算法)
应用在逻辑回归的过程:用全量特征跑一个模型;根据线性模型的系数(体现相关性),删掉5-10%的弱特征,观察准确率/auc的变化;逐步进行, 直至准确率/auc出现大的下滑停止。 python包:RFE
3)嵌入型
方法:根据模型来分析特征的重要性,最常见的方式为用正则化方式来做特征选择。
先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据权值系数从大到小来选择特征。类似于过滤法,但是它是通过机器学习训练来确定特征的优劣,而不是直接从特征的一些统计学指标来确定特征的优劣。
举例:最早在电商用LR做CTR预估, 在3-5亿维的系数特征上用L1正则化的LR模型。L1正则化有截断作用,剩余2-3千万的feature,意味着其他的feature重要度不够。
python包:feature_selection.SelectFromModel选出权重不为0的特征。
小结:特征选择是特征工程的很重要的一步,它关系到我们机器学习算法的上限。因此原则是尽量不错过一个可能有用的特征,但是也不滥用太多的特征。
五、特征提取
特征提取是通过特征转换,自动地对原始观测降维,使其特征集合小到可以进行建模的过程。 特征提取有时能发现更有意义的特征属性。
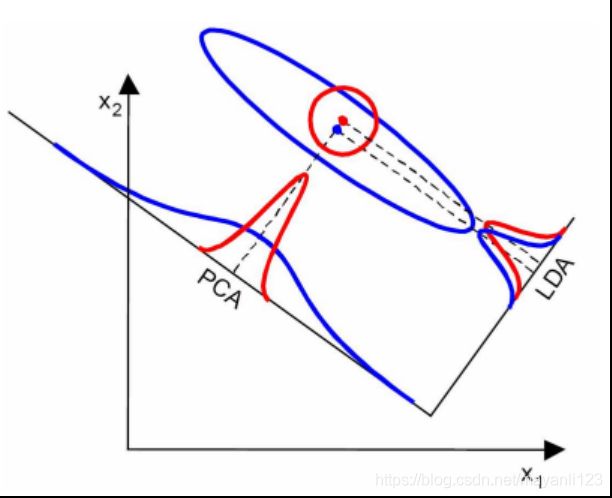
特征提取常用方法PCA、LDA
1) PCA (Principal component analysis,主成分分析)
PCA 是降维最经典的方法,它旨在是找到数据中的主成分,并利用这些主成分来表征原始数据,从而达到降维的目的。PCA 的思想是通过坐标轴转换,寻找数据分布的最优子空间。
PCA 的解法一般分为以下几个步骤:
1.对样本数据进行中心化处理;
2.求样本协方差矩阵;
3.对协方差矩阵进行特征值分解,将特征值从大到小排列;
4.取特征值前 n 个最大的对应的特征向量 W1, W2, …, Wn ,这样将原来 m 维的样本降低到 n 维。
通过 PCA ,就可以将方差较小的特征给抛弃,这里,特征向量可以理解为坐标转换中新坐标轴的方向,特征值表示在对应特征向量上的方差,特征值越大,方差越大,信息量也就越大。这也是为什么选择前 n 个最大的特征值对应的特征向量,因为这些特征包含更多重要的信息。
2)LDA (Linear Discriminant Analysis,线性判别分析)
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。
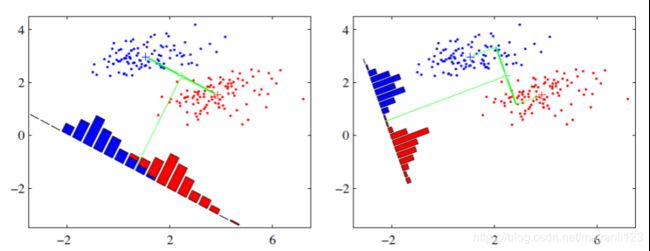
LDA的原理是将带上标签的数据(点),通过投影的方法,投影到维度更低的空间,使得投影后的点,会形成按类别区分,相同类别的点,将会在投影后更接近,不同类别的点距离越远。
LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。
3)LDA与PCA的区别
相同点:
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布。
不同点:
1)LDA是有监督的降维方法,而PCA是无监督的降维方法
2)LDA降维最多降到类别数k-1的维数,而PCA没有这个限制。
3)LDA除了可以用于降维,还可以用于分类。
4)LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。