拉呱NLP：传统文本表示（一）

计算机只能算数而无法直接理解人类语言，所以就需要将其翻译成数字以便于处理，这个翻译的过程就是 编码 。具体到每个字/词要编成啥样式、多大的数字，方法就很很多了，本篇俺就按发展历史介绍几种重要的传统文本表示方法。

1. One Hot编码

最简单的编码，我相信地球人都能想到，没错，就是每个词用一个数字ID表示，比如 【我：1，爱：2，你：3】，这样计算机见到 “我爱你”就知道是“123”，见到“321”就知道是“你爱我”。我们知道数字都是有大小的，这个时候就有问题了，大家都是汉字，凭什么你是3，我是1，所以，为了体现字字平等，天下大同，大家都是1，都是可以区分的1，怎么区分呢，三个词一商量，要不我就是100，爱是010，你是001，这样问题就解决了（当然谁是100，谁是010，都没有关系）。这就是大名鼎鼎的One Hot（独热编码）。

如图所示，一个字/词一个id/index，再转成one-hot向量。对于单词 A，它出现在词表中的位置为 k，它的向量就是“第 k 位为1，其他位置为0 ”的一个向量。
优点就很明显了：

1.可以处理非数值型的特征，在逻辑回归等传统机器学习算法上应用比较广泛
2.一定程度上可以扩充特征，比如性别这一属性，经one-hot后就成为男、女两个特征

当然缺点 也显而易见：

1.词与词是有语义关系的，one-hot显然没有考虑这种情况，每个词编码都是独立的；
2.词表有多长，每个词向量维度就有多长，造成维度灾难，计算量大，很容易OOM。

2. Bag-of-words（BOW：词袋模型）

把已有文本的所有词去重后放一个袋子里，就是BOW，没错，就是这么easy。但是怎么用呢？俺先来举个：

假设一共有这两句话，那组成的词袋去重后就包含9个词：

这时候t1、t2的表征向量长度就是9，大小用每个词的词频来表示：

t1、t2的距离：
$$length(t1,t2)=||t1-t2||=\sqrt{1+1+1+1+1+1+1+1+1}=3$$
BOW本质和one-hot是一样的，可以处理离散的非数值型数据，一定程度上扩充特征。但当文本很多时，句向量较长且很多为0，会得到一个稀疏矩阵；且词袋模型依赖词频，没有考虑词序等涉及语义的信息，文本的微小变动，也会造成很大影响，如“喜欢”前多加一个“不”字，语义完全相反但得出的结果仍然很相似。
提到文档和词频，自然就会想到TF-IDF，这是判断词的重要性算法，以后再说。

3. N-gram

语言模型的目标是啥呢？其实就是让语言字符拼起来能是一句人话，咋判断哪个字符串是最像人话的呢，没错，概率！概率越大越可能拼对了。语言模型的本质是对语句的概率分布建模。数学语言就是：
给定任意的字符串 $w_1^n=w_1{w}_2{w}_3...w_n$，计算该字符串出现的概率$p(w_1^n)$
根据贝叶斯公式，联合概率分解：
$$p(w_1^n)=p(w_1{w}_2{w}_3...w_n)=p(w_2^n|w_1)p(w_1)=p(w_1)p(w_2|w_1)p(w_2|w_1^2)...p(w_n|w_1^{n-1})=\prod _{k=1}^{n}p(w_k|w_1^{k-1})$$
其中：$$p(w_3|w_1^2)\approx \frac{count(w_1{w}_2{w}_3)}{count(w_1{w}_2)}$$
表示在词$w_1{w}_2$一起出现的条件下，$w_1{w}_2{w}_3$排列出现的概率。

举个： $\text{text}\to \text{好客山东欢迎您}$
$p(text)=p(w_1=好,w_2=客,...,w_7=您)=p(好)p(客|好)p(山|好客)p(东|好客山)...p(您|好客山东欢迎)$
$$p(山|好客)\approx \frac{count(好客山)}{count(好客)}$$
这种方式存在的问题：
1.参数空间问题：从公式可以看出，随着字符串长度增加，参数会指数级暴增（条件概率$p(w_n|w_1^{n-1})$的可能性太多），几乎不可能正确的估计这些参数。
2.数据稀疏严重(零概率/OOV问题)：对于非常多词对的组合，在语料库中都没有出现，依据最大似然估计得到的概率将会是0。而且当$count(好客山)=count(好客)$时，也不能认为$p(山|好客)=1$

为了解决问题1，引入了马尔科夫假设：随意一个词出现的概率只与它前面出现的n-1个词有关。基于该假设的统计语言模型就是N-gram语言模型。

• 当n=1时，即一个词的出现与它周围的词是独立，称为unigram。[我，爱，自，然，语，言，处，理]
• 当n=2时，即一个词的出现仅与它前面的一个词有关时，称为bigram
• 当n=3时，即一个词的出现仅与它前面的两个词有关，称为trigram

参数的数量级是n取值的指数倍，所以尽管理论上n的取值越大，效果越好。但在实践中用的最多的是bigram和trigram了，高于四元的用的非常少，由于训练它须要更庞大的语料，并且数据稀疏严重，时间复杂度高，精度却提高的不多。

n	模型参数
1(unigram)	$2\cdot 10^5$
2(bigram)	$4\cdot 10^{10}$
3(trigram)	$8\cdot 10^{15}$
4(4gram)	$16\cdot 10^{20}$

为了解决问题2，即由于语料的稀疏性，有些词序列找不到，所以需要对数据进行平滑处理，简单列几种数据平滑的方法：

• 加一平滑(拉普拉斯平滑)：将每个计数+1，使得概率为0的词序列得到一个很小的概率

  优点：算法简单，解决了概率为0的问题
  缺点：给训练语料中没有出现过的词分配了太多的概率空间，认为所有未出现的词概率相等也不合理。

• 古德-图灵平滑(Good-turing Smoothing)：用看见过1次的事情估计未看见的事件，并依次类推，用看见过2次的事件估计看见过1次的事件。$$r^{\ast }=(r+1)\frac{n_r+1}{n_r}，n_r:出现了r次n元对的个数$$
  所以N-gram中N元对$w_{i-n+1}^i$出现次数为r的概率为：$$P_{GT}(w_{i-n+1}^i)=\frac{r^{\ast }}{{\sum }_{r=0}^{\infty }{r}^{\ast }}$$
  古德-图灵估计公式中缺乏利用低元模型对高元模型插值的思想，通常不单独使用，而作为其他平滑算法中的一个计算工具。
• 回退平滑(Katz smoothing)：古德-图灵的改进版，当某一事件在样本中的概率大于阈值K（通常取0或1）时，运用最大似然估计的减值法来估计其概率。否则使用低阶的，即用 (n−1)gram的概率来替代n−gram的概率，这种替代受归一化因子$\alpha$的作用。$$P_{KATZ}(w_{i-1}^i)=\{\begin{array}{l}{d}_r\frac{c(w_{i-1}^i)}{c(w_i-1)}，c(w_{i-1}{w}_i)=r>0\\ \alpha (w_{i-1})P_{ML}(w_i)，c(w_{i-1}{w}_i)=r=0\end{array}$$
  其中$r$表示出现次数，$P_{ML}(w_i)$表示$w_i$的最大似然估计概率，折扣率$d_r$ 近似等于$\frac{r^{\ast }}{r}$，减值由古德-图灵估计方法预测。
• 线性插值平滑(Jelinek Mercer)：利用低阶N-gram模型对高阶N-gram模型进行线性插值。$$P_{interp}(w_i|w_{i-n+1}^{i-1})={\lambda }_{w_{i-n+1}^{i-1}}\ast P_{ML}(w_{i-1}|w_{i-n+1}^{i-1})+(1-\lambda )\ast P_{interp}(w_i|w_{i-n+2}^{i-1})$$
  N-gram模型可以递归地定义为：由最大似然估计得到的N-gram模型和线性插值的 (N-1)-gram模型。

N-gram语言模型的优点：

1.bigram，trigram 实现简单，能够很好地应用在一些经典场景中，例如检查拼写错误（极大似然句子概率）
2.常见搜索引擎的输入下拉帮助，就是通过n-gram来实现的
3.可解释性强，易于理解和调试。
4.易于增量实现和并行训练。

N-gram语言模型的缺点：

1. 需要解决数据稀疏性的问题，需要利用平滑算法。
2. 由于是离散型变量，没有办法度量词语之间相似度。
3. 模型巨大，与|V| 词库大小呈指数增长。

4. NNLM（神经网络语言模型）

讲N-gram的时候，我们已经提到链式概率法则：$$p(w_1^n)=p(w_1)p(w_2|w_1)p(w_2|w_1^2)...p(w_n|w_1^{n-1})=\prod _{k=1}^{n}p(w_k|w_1^{k-1})$$
根据马尔科夫假设，当前词只与前$m$个词有关：
$$p(w_1^n)\approx \prod _{k=1}^{n}p(w_n|w_{n-m+1}^{n-1})$$$$w_n：要预测的词w_{n-m+1}^{n-1}=w_{n-m+1},...,w_{n-1}：w_n前面的历史词语$$
对上式进行建模，常采用极大似然估计，将目标函数设为：$$L=\sum logp(w_n|w_{n-m+1}^{n-1})$$对该函数进行最大化，可见概率$p(w_n|w_{n-m+1}^{n-1})$已被视为$w_n$关于$w_{n-m+1}^{n-1}$的函数：$$p(w_n|w_{n-m+1}^{n-1})=F(w_n,w_{n-m+1}^{n-1},\theta ),\theta 表示待定参数集$$这种方法相较于$N-gram$不需要先计算并保存所有的概率值，而是对函数$F$进行优化得到最优的${\theta }^{\ast }$就可以了，且${\theta }^{\ast }$的量级远小于$N-gram$的参数量。
$\text{关键问题是函数F的构造，下面的NNLM就是通过神经网络来来构造F。}$
$NNLM也是word2vec算法的基础$

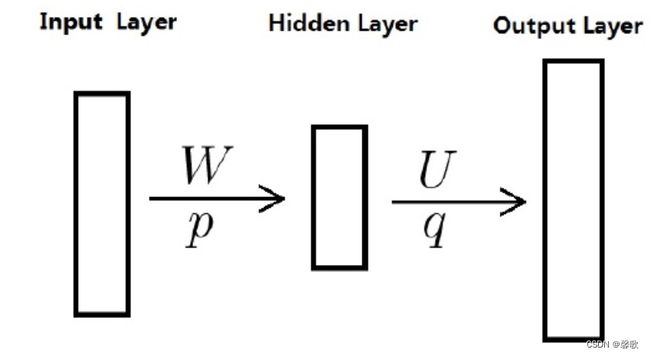
NNLM来源于Bengio等人2003年的论文《A neural probabilistic language model . Journal of Machine Learning Research》,该论文提出的神经概率语言模型也用到了词向量一词。NNLM是一个简单易懂的模型，4层结构输入层(Input Layer)、投影层(Projection Layer)、隐藏层（Hidden Layer）、输出层（Output Layer）

对于语料$C$中的任意词$w$，$Context(w)$表示其前面的$n-1$个词，这样的二元组$(w,Context(w))$为一个样本，对于一句话中前面几个词，其前面不够$n-1$个词，填充几个向量就好了，它们也参与训练。
其实更多时候，我们将其视为三层的网络结构，看个人怎么理解：

Bengio还考虑了输出层和投影层之间边相连的情况，这样无非是二者之间多了一个权重矩阵，有没有都不影响对算法本质的理解，只是作者发现多加入一个权重矩阵，虽然效果没有提升，但收敛速度会加快，减少迭代次数。
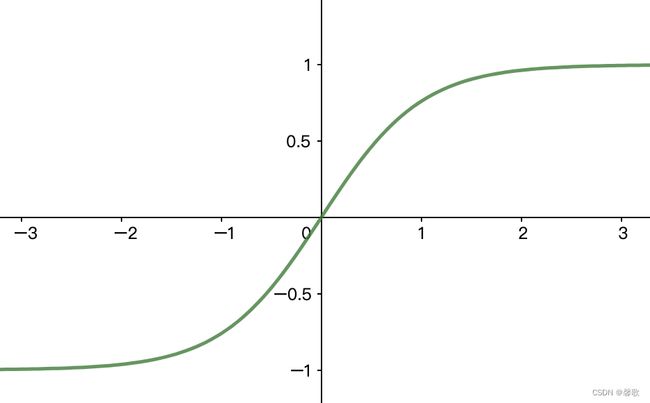
给定语料$C$和设定词向量的长度$l$之后，投影层和输出层的规模就确定了$\text{(}n-1)\cdot l$，因为输入层包含$Context(w)$中的$n-1$个词，而投影层的$X_w$则是由$n-1$个词向量首尾拼接起来的长向量，长度为$(n-1)\cdot m$，计算过程为：$$\{\begin{array}{l}{Z}_w=tanh(W_{X_w}+p)\\ Y_w=U_{Z_w}+q\end{array}$$$tanh$：双曲正切函数，作为隐藏层的激活函数。$$tanhx=\frac{sinhx}{coshx}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

经过计算得到的$Y_w=(y_{w1},y_{w2},y_{w3},...,y_{wn}{)}^T$是长度为$N$(词汇表的长度)的向量，其分量$y_{wi}$还不能表示概率，如果要$y_{wi}$表示当上文为$Context(w)$时下文正好是$D$(词汇表)中的第$i$个词时，还需要$softmax$归一化，即$$P(w|Context(w))=\frac{e^{y_{w,i_w}}}{{\sum }_{i=1}^N{e}^{y_{wi}}}$$$i_w$表示词$w$在词典$D$中的索引。
下面这张图则来自Benjio的论文：

该神经网络需要确定的参数就是我们前面提到的${\theta }^{\ast }$，在投影层和隐藏层，其实参数量还是比较大的，后面的$word2vec$就有对这部分的优化工作。
与$N-gram$模型相比，NNLM的优点主要体现在2个方面：
①词语之间的相似性可以通过词向量来体现。举个：如果 $t1=$“狗坐在沙发上看电视”这句话出现了$1000$次，而 $t2=$“猫坐在沙发上看电视”只出现$1$次，用$N-gram$的话，概率$p(t1)$明显大于$p(t2)$，但$p(t1)$、$p(t2)$应该很相近才对。在神经网络语言模型中，有一个假定，就是$拥有了相似上下文的词语也应该有相似的语义$，同时概率函数关于词向量是光滑的，即词向量的一个小变化对概率的影响也是小变化。
②该词向量模型自带平滑功能，不会出现像$N-gram$那样概率为0的情况。
缺点：
①计算量巨大，主要在于两个大矩阵的乘法；
②静态词向量的通病：没有解决一词多义；
③网络的输入窗口为固定值，不能更改；
④整个网络的参数，也是随着词表的增大呈线性增长的。

可以看到，NNLM模型中的词向量是模型训练过程中，目标函数的辅助参数，训练结束后，其实只是模型的一个副产品，但这个副产品很重要。事实上，大部分情况下，词向量和语言模型都是捆绑在一起的，训练后二者同时得到。

参考链接：
1.https://blog.csdn.net/qq_42734492/article/details/109076898
2.https://zhuanlan.zhihu.com/p/265716548
3.https://zhuanlan.zhihu.com/p/111534577
4.https://cloud.tencent.com/developer/news/455980
5.https://blog.csdn.net/u010379324/article/details/79564605
6.https://blog.csdn.net/itplus/article/details/37969519