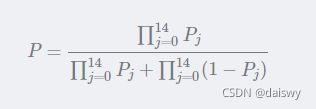贝叶斯算法：垃圾邮件过滤

准备
    100封邮件，50封垃圾邮件和50封正常邮件
参考 :
    贝叶斯算法原理

程序过程解释
垃圾邮件分类的数学基础是贝叶斯推断(bayesian inference)。整个程序过程主要有以下几个部分构成：

step 1 : 提取邮件并处理
1、使用 TDirectory.GetFiles(xPath) 获得 xPath 指示的文件夹下的所有文件的路径。
2、用 TStringList 根据路径读取文件内容。
3、使用 Split 方法将TStringList读取的内容以空格和“#13”分割开，并将所有单词放入数组中。

以上三个步骤全部包含在  getEmail(emailClass) 函数 和 processEmail(emailpath) 函数中。

step 2 : 获得在 normal 和 junk中每个单词的频数
这个步骤在代码中只是一个函数 getWordFrequency(emailClass) 。emailClass 表示邮件类别，即 normal 或者 junk 。返回的是一个字典，字典的 key值是单词，value值是这个单词的频数。

注意，这里的频数并不是指这个单词出现了多少次，而是指这个单词在多少封邮件当中出现过。例如：一个单词 sex 出现在3封邮件中，分别出现了5次，6次，4次，则这个单词 sex 的频数我们这里确定为3(因为它出现在3封邮件中),而不是 5 + 6+ 4 = 15 。

step 3 : 计算每个单词的后验概率
这一段代码包含在(某种意义上的)“主函数”当中 ：

1、通过step 1和 step 2定义的函数取得 normal 和 junk 中每个单词的频数;
2、创建单词的先验概率字典 GPosteriorProbabilityDict ，并初始化每一个单词的先验概率为0.00;
3、使用 for...in... 循环得到每个单词的先验概率：

     P(S|W) = P(W|S)P(S) / P(W|S)P(S) + P(W|H)P(H)
     
因为 normal 和 junk 的邮件数量相同，所以其先验概率 P(S) 和 P(H) 是相同的，均为 50%, 所以公式简化为 ：

     P(S|W) = P(W|S) / P(W|S) + P(W|H)

在代码中 P(W|S) 用 xJunkPro 变量表示， P(W|H)用 xNormalPro 表示。

如果当前单词在某个类别当中没有出现过，则可规定这个单词在这个类别中的后验概率是 0.01。

step 4 : 分类函数
这步骤主要体现在  testEmail(emailpath, threshold = 0.7) 函数中。email 参数表示email文件， threshold参数表示阀值，当计算得到的结果大于threshold时表示这是一封垃圾邮件(junk)， 否则这是一封正常邮件(normal), 这里默认 threshold = 0.7。

对于给定的测试email，计算过程如下 ：

1、使用 processEmail() 函数处理得到这封email的单词集合xWordArr 。
2、将这封邮件中每个单词和它的后验概率放入数组 xPosteriorProbabilityArr 中 ，如果这个单词在字典 GPosteriorProbabilityDict 中并没有出现过，则指定其值为 0.4。
3、按照每个单词的概率值从小到大排序。
4、最后，计算联合概率。这里只取出先验概率最大的前15个词计算联合概率，公式为：

                                

这里  用 变量xFracTop 在for...in...循环中累乘表示， 用变量xFracBottom累乘表示 。 

6、返回判定结果，如果xFracTop / (xFracTop + xFracBottom) 的值大于阀值threshold则判定为junk， 否则判定为 normal 。

step 5 : 准备工作完成，开始测试
对新收到的邮件进行测试，将收到的邮件存为txt文件，把路径赋给testEmail()函数中进行测试。然后，就等待判定结果。

完整代码

uses System.Generics.Collections ,System.Generics.Defaults;

type
  TArrayB = array of TArray ;

# step 1 : get E-mail and process them

class function TJunkBayes.processEmail(emailpath: string): TArray ;
var
  xWordLst: TStringList ;
  xWordArr: TArray ;
const xSep: array[0..1] of string = (' ' ,#13);
begin
  xWordLst := TStringList.Create ;
  xWordLst.LoadFromFile(emailpath) ;
  xWordArr := xWordLst.Text.Split(xSep) ;
  Result := xWordArr ;
end;

class function TJunkBayes.getEmail(emailClass: string): TArrayB ;
var
  xPath: string ;
  I : Integer ;
  xFileArr: TArray ;
  xEmailArr : TArrayB ;
  xLen: Integer ;
begin
  xPath := g_BayesPath + '\' + emailClass ;
  xFileArr := TDirectory.GetFiles(xPath) ;
  xLen := Length(xFileArr) ;
  SetLength(xEmailArr ,xLen);
  for I := Low(xFileArr) to High(xFileArr) do
    begin
      xEmailArr[I] := processEmail(xFileArr[I]) ;
    end;
  Result := xEmailArr ;
end;

# step 2 : get word frequency of the email's class

class function TJunkBayes.getWordFrequency(emailClass: string): TDictionary ;
var
  xWordFrequencyDict : TDictionary ;
  xEmailArr: TArrayB ;
  I ,k: Integer;
  xWord : string ;
  xWordLst: TStringList ;
begin
  xEmailArr := getEmail(emailClass) ;
  xWord := '';
  xWordLst := TStringList.Create ;
  xWordFrequencyDict := TDictionary.Create();
  for I := Low(xEmailArr) to High(xEmailArr) do  //遍历每封邮件
    begin
      xWordLst.Clear ;
      for k := Low(xEmailArr[I]) to High(xEmailArr[I]) do  //遍历一封邮件里的内容
        begin
          xWord := Trim(LowerCase(xEmailArr[I][k])) ;
          if xWord = '' then Continue ;
          if xWordLst.IndexOf(xWord) = -1 then
            xWordLst.Add(xWord) ;
        end;
      for k := 0 to xWordLst.Count - 1 do
        begin
          xWord := xWordLst[k] ;
          try
            xWordFrequencyDict.Items[xWord] := xWordFrequencyDict.Items[xWord] + 1 ;
          except
            xWordFrequencyDict.Add(xWord ,1) ;
          end;
        end;
    end;
  Result := xWordFrequencyDict ;
end; 

# step 4 : calculate classified result of test email

class function TJunkBayes.TestEmail(emailpath: string ;Threshold: Double) : Boolean ;
var
  xWordArr: TArray ;
  xWord : string ;
  xProbability : Double ;
  xPosteriorProbabilityArr: array of Double ;
  xCount: Integer ;
  I : Integer ;
  xFracTop,xFracBottom : Double ;
begin
  Result := False ;
  xWordArr := processEmail(emailpath) ;
  SetLength(xPosteriorProbabilityArr ,Length(xWordArr));
  xCount := 0 ;
  for xWord in xWordArr do
    begin
      try
        xProbability := GPosteriorProbabilityDict[xWord] ;
      except //当这个单词不存在时
        xProbability := 0.4 ;
      end;
      xPosteriorProbabilityArr[xCount] := xProbability ;
      xCount := xCount + 1;
    end;
  TArray.Sort(xPosteriorProbabilityArr); //从小到大排序
  xFracTop := 1 ;
  xFracBottom := 1 ;
  for I := High(xPosteriorProbabilityArr) downto Length(xPosteriorProbabilityArr) - 15 do
    begin
      xFracTop := xFracTop * xPosteriorProbabilityArr[I] ;
      xFracBottom := xFracBottom * (1 - xPosteriorProbabilityArr[I]) ;
    end;
  if (xFracTop / (xFracTop + xFracBottom) > Threshold) then
    Result := True
  else
    Result := False ;
end;

#step 3: calculate posterior probability

class procedure TJunkBayes.CalculateWordPosteriorProbability ;
var
  xNormalDict: TDictionary ;
  xJunkDict: TDictionary ;
  xNormalEmailCount ,xJunkEmailCount: Integer ;
  xWord : string ;
  I: Integer;
  xNormalPro ,xJunkPro : Double ;
begin
  xNormalEmailCount := Length(TDirectory.GetFiles(g_BayesPathNormal)) ;
  xJunkEmailCount := Length(TDirectory.GetFiles(g_BayesPathJunk)) ;
  GPosteriorProbabilityDict := TDictionary.Create() ;
  //正常邮件集 里所有的单词和频数
  xNormalDict := getWordFrequency('NormalBayes') ;
  //垃圾邮件集里所有的单词和频数
  xJunkDict := getWordFrequency('JunkBayes') ;
  for xWord in xNormalDict.Keys do
    begin
      GPosteriorProbabilityDict.Add(xWord ,0);
    end;
  for xWord in xJunkDict.Keys do
    begin
      try
        GPosteriorProbabilityDict.Add(xWord ,0);
      except
      end;
    end;
  for xWord in GPosteriorProbabilityDict.Keys do
    begin
      try
        xNormalPro := xNormalDict[xWord] / xNormalEmailCount ;
      except
        xNormalPro := 0.01 ;
      end;
      try
        xJunkPro := xJunkDict[xWord] / xJunkEmailCount ;
      except
        xJunkPro := 0.01 ;
      end;
      GPosteriorProbabilityDict[xWord] := xJunkPro / (xNormalPro + xJunkPro) ;
    end;
end;

#step 5 : test start

调用以下两个过程

TJunkBayes.CalculateWordPosteriorProbability ;
TJunkBayes.TestEmail('testemailpath' ,0.7) ;