基于 Python 的自然邻域法空间插值的实现与思考

   自然邻域法是基于区域大小按比例对这些样本应用权重来进行插值 (Sibson 1981)，该插值也称为 Sibson 或“区域占用 (area-stealing)”插值。其基本属性是它具有局部性，仅使用查询点周围的样本子集，并保证插值高度在所使用的样本范围之内，插值表面将通过输入样本且在除输入样本位置之外的其他所有位置均是平滑的。

0.原理

  自然邻域法的基础原理是加权平均，其数据基础如下：

$$f_{(X,Y)}=\sum _{i=1}^k{w}_i{x}_i,$$

  其中 $f_{(X,Y)}$ 为坐标 X,Y 位置的插值结果，$x_i$ 为第i个参与插值的原始数据的真值，$w_i$为$x_i$值对应的权重。

  明确了自然邻域法的插值原理，那么选择参与插值的真值$x_i$及其对应的权重$w_i$就是实现自然邻域法插值的主要目标！

0.1 泰森多边形

  这里用到 泰森多边形 来确定参与插值的真值及其权重。

泰森多边形又叫冯洛诺伊图（Voronoi diagram），得名于Georgy Voronoi，是一组由连接两邻点线段的垂直平分线组成的连续多边形。一个泰森多边形内的任一点到构成该多边形的控制点的距离小于到其他多边形控制点的距离。

  泰森多边形示例（依据本套测试数据构建）：

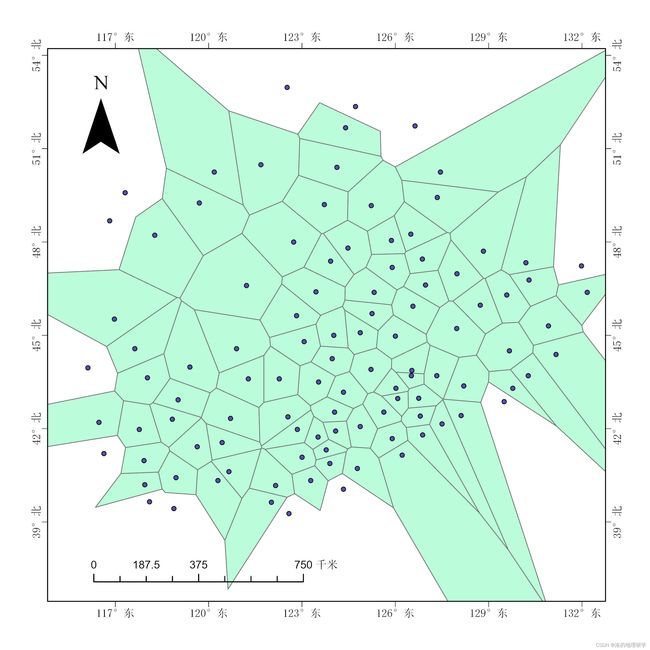
  其中每个泰森多边形中都包含一个真值（本例中舍弃了无界区域）。

0.2 公式在空间上的理解

  针对原理公式，其在泰森多边形的理解如下：

  其中 $f_{(X,Y)}$ 为坐标 X,Y 位置的插值结果，红色多边形为插值点所在的泰森多边形（通过将插值位置加入原始数据中，构造新的泰森多边形，新泰森多边形的顶点与原始数据构造泰森多边形不重复的顶点就是插值点所在泰森多边形的顶点），面积为$S$，其与原始数据构造的泰森多边形中①、②、③、④、⑤五个多边形相交，每个多边形内都有一个对应的真值$x_i$。
  以第一个多边形为例，其中多边形内点真值为$x_1$，多边形①与粉色多边形交集的面积为$I{n}_1$。那么，第一个真值$x_1$对应的权重$w_1=I{n}_1/S$。

参考文献

• Sibson, R. (1981). “A brief description of natural neighbor interpolation (Chapter 2)”. In V. Barnett (ed.). Interpolating Multivariate Data. Chichester: John Wiley. pp. 21–36.
• V.V. Belikov; V.D. Ivanov; V.K. Kontorovich; S.A. Korytnik; A.Y. Semenov (1997). “The non-Sibsonian interpolation: A new method of interpolation of the values of a function on an arbitrary set of points”. Computational mathematics and mathematical physics. 37 (1): 9–15.
• N.H. Christ; R. Friedberg, R.; T.D. Lee (1982). “Weights of links and plaquettes in a random lattice”. Nuclear Physics B. 210 (3): 337–346.

1.思路

1. 构造原始数据的泰森多边形。
2. 构造插值数据的位置数组，记录插值坐标（X,Y）。
3. 计算每一个插值坐标与原始数据组成的具有不重复泰森多边形顶点的插值多边形。
4. 计算权重，并按照公式计算 $f_{(X,Y)}$。
5. 整理结果，写出栅格。

2.实现

测试数据下载链接：https://pan.baidu.com/s/1P57gQtyvGzonB–jW_jU1A?pwd=0qk5
提取码：0qk5

  按照如上思路，这里开始设计代码实现：

2.1 主要步骤

from collections import namedtuple
import numpy as np
from scipy.spatial import Voronoi
from osgeo import ogr
from gma.math import ToNumericArray

class IPolate:
    '''以下代码进行了简化！今后 gma 会合入的并非此版本！'''
    def __init__(self, Points, Values, Boundary, Resolution):
        ## 这里主要对输入点和值进行检查，并根据插值边界 Boundary 和空间分辨率返回插值数组
        self.Points, self.Values = Points, Values
        ## 初始化边界和分辨率
        self.Left, self.Bottom, self.Right, self.Top = Boundary
        self.Resolution = Resolution
        ## 构造仿射变化
        self.Transform = (self.Left, self.Resolution, 0, self.Top, 0, -self.Resolution)
        ## 生成插值数组
		IPolate._GetRangeArray(self)
        
    def _GetRangeArray(self):
        '''生成目标经纬度数组及长宽！'''
        LON = np.arange(self.Left, self.Right + self.Resolution, self.Resolution)
        LAT = np.arange(self.Top, self.Bottom - self.Resolution, -self.Resolution)
        
        self.XLON, self.YLAT = len(LON), len(LAT)

        self.XYs = ToNumericArray(np.meshgrid(LON, LAT)).reshape(2, self.XLON * self.YLAT).T
        
    def _VertexPolyMap(self):
        '''生成顶点多边形'''
        PointRegion = self.VOR.point_region
        Regions = self.VOR.regions
        
        VertexPolyMap = []
        NumLOC = []

        for i, ar in enumerate(self.Points):
            Index = np.where(PointRegion == i)[0][0]
            Region = Regions[i]
            if -1 not in Region and Region != []:
                VertexPolyMap.append(CreatePolygon(OrderPoly(self.Vertices[Region])))
                NumLOC.append(Index)    
        return NumLOC, VertexPolyMap       

    def NaturalNeighbor(self):
        """自然邻域法插值。"""
        
        # 生成泰森多边形
        self.VOR = Voronoi(self.Points, incremental = True)
        
        # 顶点
        self.Vertices = self.VOR.vertices
        
        # 生成顶点多边形
        NumLOC, VertexPolyMap = IPolate._VertexPolyMap(self) 
        
        # 生成插值数组
        NNResult = np.zeros(len(self.XYs))
        
        for i, ar in enumerate(self.XYs):
            vor = Voronoi(self.Points, incremental = True)
            vor.add_points(np.array([ar]))
            vor.close()

            # 去除重复顶点
            NewVertices = vor.vertices # 新顶点
            New = np.array([NV for NV in NewVertices if NV not in self.Vertices])
            
            # 少于3个点无法构造多边形 
            if len(New) < 3:
                NNResult[i] = np.nan
                continue

            # 计算新面积
            NewPolygon = CreatePolygon(OrderPoly(New))
            NewPolygonArea = NewPolygon.Area()

			# 这里主要考虑了边界处处理的问题，对公式进行了重新的定义
            WeightsArea = np.array([NewPolygon.Intersection(VPM).Area() for VPM in VertexPolyMap])
            
            # 重置面积
            NewPolygonArea = np.min([WeightsArea.sum(), NewPolygonArea])
            
            # 计算插值结果    
            NNResult[i] = (self.Values[NumLOC] * WeightsArea).sum() / NewPolygonArea
            
        NT = namedtuple('NaturalNeighbor', ['Data', 'Transform'])
    
        return NT(NNResult.reshape(self.YLAT, self.XLON), self.Transform)

2.2 关联函数

def OrderPoly(Points):
    """有序多边形。按顺时针方向排列 Points 多边形的顶点!"""
    MeanX, MeanY = np.mean(Points, axis = 0)
    def Condition(x):
        return np.rad2deg(np.arctan2(x[0] - MeanX, x[1] - MeanY))
    return sorted(Points, key = Condition)

def CreatePolygon(Points):
    '''创建多边形'''
    Polygon = ogr.Geometry(ogr.wkbPolygon)
    
    LR = ogr.Geometry(ogr.wkbLinearRing)
    for XY in Points: 
        LR.AddPoint(*XY)
    LR.CloseRings()
    
    Polygon.AddGeometry(LR)
    return Polygon

2.3 插值测试

import pandas as pd
import gma

# 读取数据
Data = pd.read_excel("IDW.xlsx")
Points = Data[['经度','纬度']].values
Values = Data['值'].values
# 插值
NN = IPolate(Points, Values, Boundary=(116.12, 39.27, 132.97, 52.97), Resolution = 0.1)
MMD = NN.NaturalNeighbor()
# 写出栅格
gma.rasp.WriteRaster(r".\gma_NN3.tif",MMD.Data,Projection = 'WGS84', Transform = MMD.Transform, DataType=6)

3.总结

3.1 与ArcGIS对比

  整体而言，与ArcGIS相同分辨率、范围下的插值结果对比（对比图如下），显然以上代码效果较差。从对比中可以发现：

1. 中心处点密集区域，上述方法插值结果与ArcGIS结果值相同或相近，证明上述方法思路和过程正确。
2. 上述方法的插值结果范围内有空值，而ArcGIS没有，可能是ArcGIS做了其他的一些处理。
3. ArcGIS插值结果仅包含了最外层点组成的面内的数据，显然，边界外的数据插值结果异常值较多。
4. 上述方法边界处插值较差（例如下图左，左下角），仍有需要改进的地方。
   

3.2 一些思考

  （1）保证插值数据。与其他插值方法相同，使用任何空间插值方法进行数据插值，都要尽可能多的使用真实值，并且要包含边界外的一些数据，以提高研究范围内边界处数据的插值精度。
  （2）空值处理。ArcGIS的功能或算法已经相当完善，既然要自行构建代码，必须要学习ArcGIS对于异常的处理的优势。当然，目前尚不清楚ArcGIS使用了什么样的优化方式，也希望各路大神提供思路和改进意见。
  （3）优化处理。实际上，在非中心区域插值点新泰森多边形也存在如下情况，在插值代码中以作矫正处理，矫正原理是舍弃粉色多边形不与原始数据的泰森多边形相交的部分，但优化结果有限。

  （4）面积计算。这里直接使用了 WGS 84坐标系计算面积，其单位是平方度，一定程度上会降低插值精度。

4.反馈与讨论

微信号：Luo_Suppe