Transformer详解

1.整体结构

Transformer[1]模型是Google2017年提出的一种用于机器翻译的模型，完全摒弃了传统循环神经网络的结构，采用了完全基于注意力机制的结构，取得了相当显著的效果，并且从此使得完全注意力机制这种模型设计模型从NLP领域出圈到计算机视觉领域，比如VIT就是基于Transformer的一种视觉模型，终结了CNN多年在图像领域的统治地位。
本文主要参考了李沐大佬的《动手学深度学习》，在此基础上加上了个人的见解以及代码的注释。

[1] Vaswani, Ashish , et al. “Attention Is All You Need.” arXiv (2017).

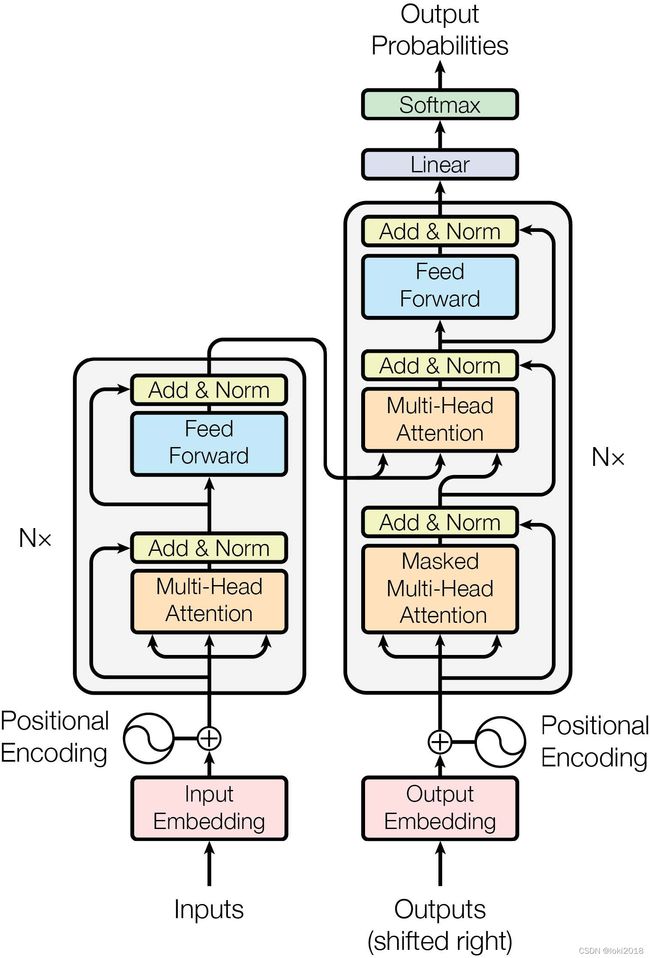
论文提出的Transformer模型结构如图所示，它的结构非常简单，分为编码器和解码器。编码器和解码器的结构也非常类似。
编码器从下向上：输入先经过embedding层，再加上位置编码，在经过多头注意力之后再通过一个残差连接并进行Layer Norm，最后再经过前馈神经网络，残差加Layer Norm。其中位置编码，多头注意力，前馈神经网络组成的块称为一个Transformer块，编码器可以由若干Transformer块构成。解码器同理，这里就不加赘述。后面就开始一步步实现Transformer块以及将若干块拼接在一起的Transformer。

2. 位置编码

由于Transformer采用的是自注意力机制，因此相较于传统的RNN,LSTM,GRU等循环神经网络没有了位置先后的信息，因为注意力机制的计算是计算的当前词元与整个句子中每个字符的注意力权重，因此即使打乱了整个句子，注意力权重的计算结果也是相同的。所以，为了赋予其位置信息，需要对输入的信息进行位置编码。

假设输入的$X\in {\mathbb{R}}^{n\times d}$，表示输入n个有d维特征的词元。加上位置编码$P\in {\mathbb{R}}^{n\times d}$，输出$X+P$。其中，$P$的计算公式如下所示：
$$P_{i,2j}=sin(\frac{i}{10000^{2j/d}})$$
$$P_{i,2j+1}=cos(\frac{i}{10000^{2j/d}})$$
根据公式，只需要对X的每个词元的偶数维度和奇数维度分别加上$sin$和$cos$的计算结果即可。那么，代码实现如下：

class PositionalEncoding(nn.Module):

    def __init__(self, num_hiddens, max_length=1000, dropout=0.5):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 构造P矩阵
        X = torch.arange(max_length, dtype=torch.float32).reshape(-1, 1) / \
            torch.pow(10000, torch.arange(0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
        # X[max_len, num_hiddens//2]
        self.P = torch.zeros(size=(1, max_length, num_hiddens))
        self.P[:,:,0::2] = torch.sin(X)
        self.P[:,:,1::2] = torch.cos(X)

    def forward(self,X):
        #X[batchsize, seq_len, num_hiddens]
        X = X + self.P[:,:X.shape[1],:].to(X.device)
        return self.dropout(X)
encoding_dim, seq_len = 16, 20
pos = PositionalEncoding(encoding_dim)
pos.eval()
X = torch.randn(size=(1, seq_len, encoding_dim))
pos(X).shape

输出的形状为：

torch.Size([1, 20, 16])

3. 注意力机制

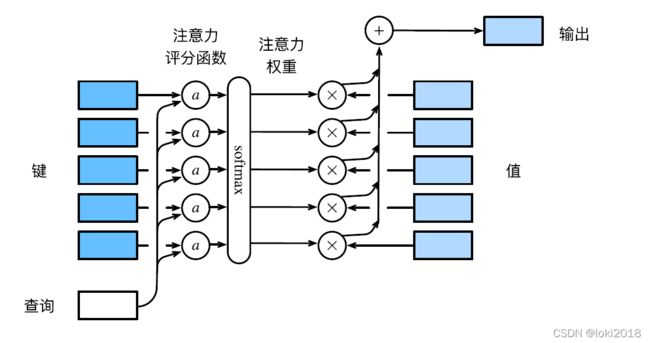
注意力机制的原理就是利用输入(查询，q)和模型中的输出(键-值, k-v)计算加权平均，这里可能会比较抽象，但是，具体的模型的qkv指代的东西都不一样，例如经典的基于循环神经网络的Seq2Seq模型，q指的是解码器的输入，k和v则是编码器每个时间步的输出，其中k和v其实是等价的，q和每个时间步的k计算相似度，再分别对每个v进行加权平均就是最终的结果。

用数学语言来描述，假设查询$q\in {\mathbb{R}}^q$, m个键值对$(k_1,v_1),(k_2,v_2),....,(k_m,v_m)$,其中$k_i\in {\mathbb{R}}^k$,$v_i\in {\mathbb{R}}^v$，注意力汇聚函数可以表示为:
$$f(q,(k_1,v_1),...,(k_i,v_i))=\sum _{i=1}^m\alpha (q,k_i)v_i$$
其中：
$$\alpha (q,k_i)=softmax(\alpha (q,k_i))=\frac{exp(\alpha (q,k_i))}{{\sum }_{j=1}^{m}exp(\alpha (q,k_j))}$$

在实际的操作中，由于文本序列长度不一致，通常使用一些无关的词元进行填充，因此在做注意力计算的时候需要将这些填充的词元进行遮蔽，这种带遮蔽的操作也同样应用于Transformer的解码器的输入，因此需要实现一个带遮蔽的softmax函数，代码如下：

def mask(X, valid_lens, value=0):
    #X[batchsize*查询个数, 键值对个数]
    #validlens[查询个数*batchsize]
    mask = torch.arange(X.shape[-1], dtype=torch.float32, device=X.device).reshape(1,-1) < valid_lens.reshape(-1, 1)
    #mask[查询个数*batchsize, 键值对个数]
    X[~mask] = value
    return X

def masked_softmax(X, valid_lens):
    #X[batchsize, 查询个数, 键值对个数]
    if valid_lens is None:
        return X
    shape = X.shape
    if valid_lens.dim() == 1:
        valid_lens = torch.repeat_interleave(valid_lens, shape[1])
    elif valid_lens.dim() == 2:
        valid_lens = valid_lens.reshape(-1)
    score = mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6).reshape(shape[0], shape[1], -1)
    return nn.functional.softmax(score, dim=-1)
 
 masked_softmax(torch.rand(2, 2, 4), torch.tensor([1, 2]))

输出为:

tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
[1.0000, 0.0000, 0.0000, 0.0000]],
[[0.6334, 0.3666, 0.0000, 0.0000],
[0.6577, 0.3423, 0.0000, 0.0000]]])

接下来，主要介绍两种主要的计算注意力权重的方式：

1. Additive Attention

加性注意力机制常用于$q$和$k$维度不同的情况，需要通过矩阵投影至相同的维度再相加，假设$q\in {\mathbb{R}}^q$, $k\in {\mathbb{R}}^k$，那么注意力评分函数可以写为：
$$a(q,k)=w_v^{T}tanh(W_{q}q+W_{k}k)$$
其中，$W_q\in {\mathbb{R}}^{h\times q}$,$W_k\in {\mathbb{R}}^{h\times k}$和$w_v\in {\mathbb{R}}^h$是可学习的参数。代码如下：

class AdditiveAttention(nn.Module):

    def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
        self.W_v = nn.Linear(num_hiddens, 1, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens):
    	# queries[batchsize, 查询个数, q的维度]
        # keys[batchsize, 键值对个数, k的维度]
        # values[batchsize, 键值对个数, v的维度]
        queries, keys = self.W_q(queries), self.W_k(keys)
        # 维度扩展：
        # queries[batchsize, 查询个数, 1, num_hiddens]
        # key[batchsize, 1, 键值对个数，num_hiddens]
        features = queries.unsqueeze(2) + keys.unsqueeze(1)
        features = torch.tanh(features)
        # features[batchsize, 查询个数，键值对个数,num_hiddens]
        scores = self.W_v(features).squeeze(-1)
        # scores[batchsize, 查询个数, 键值对个数]， 这样就计算出了每个q对应的每个k的注意力分数，接着做一个归一化	即可
        self.attention_weights = masked_softmax(scores, valid_lens)
        # 输出[batchsize, 查询个数, v的维度]
        return torch.bmm(self.dropout(self.attention_weights), values)
 
queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(2,1,1)
valid_lens = torch.tensor([2, 6])
attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8,dropout=0.1)
attention.eval()
attention(queries, keys, values, valid_lens)

2. DotProduct Attention

当$q$和$k$维度相同时，我们通常使用缩放点积注意力，由于没有学习的参数，因此它的效率也更高，并且Transformer中的自注意力机制使用的就是这种计算方式，计算公式如下：
$$a(q,k)=q^{T}k/\sqrt{(}d)$$
其中$d$为维度，代码如下：

class DotProductAttention(nn.Module):

    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens=None):
        # queries[batchsize, 查询个数, d]
        # keys[batchsize, 键值对个数, d]
        # values[batchsize, 键值对个数, 值的维度]
        d = queries.shape[-1]
        scores = torch.bmm(queries, keys.permute(0, 2, 1)) / math.sqrt(d)
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)

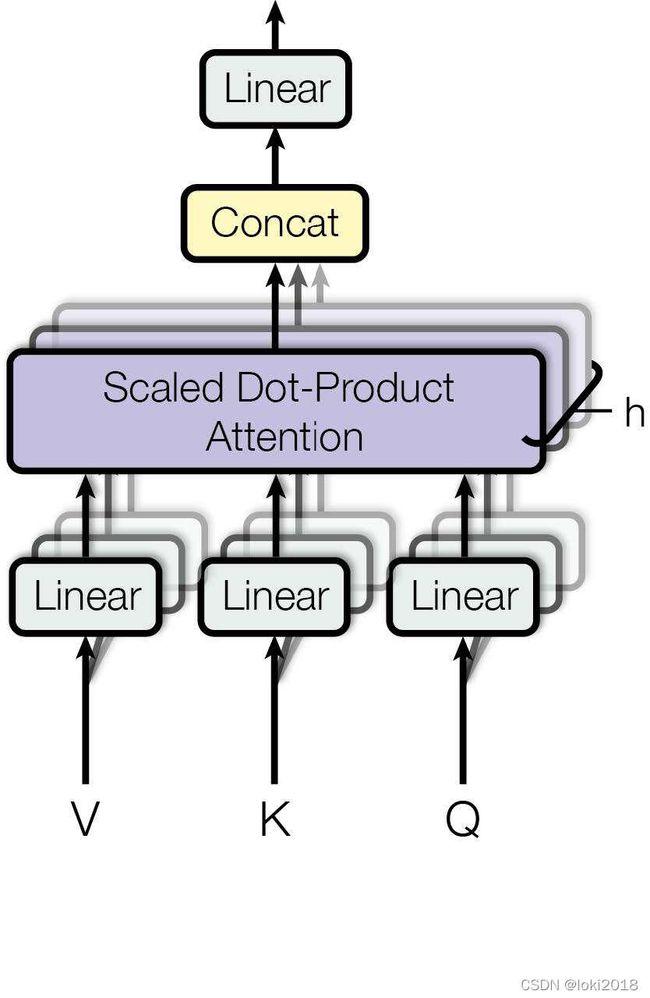
4. 多头注意力机制

类似于CNN中的多通道，在Transformer中也需要做多次注意力来获取不同的注意力，原理上来看非常简单，就是把上面的注意力计算方法计算多次，但是在代码里为了并行计算，通常会把经过线性投影后的qkv的最后一维进行分割，代码如下：

# 分头操作
def transpose_qkv(X, num_heads):
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
    # X[batchsize, seq_len, num_heads, num_hiddens/num_heads]
    X = X.permute(0, 2, 1, 3)
    return X.reshape(-1, X.shape[2], X.shape[3])

def transpose_output(X, num_heads):
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    # X[batchsize, num_heads, seq_len, num_hiddens/num_heads]
    X = X.permute(0,2,1,3)
    return X.reshape(X.shape[0], X.shape[1], -1)

class MultiHeadAttention(nn.Module):

    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        self.num_heads = num_heads
        self.attention = DotProductAttention(dropout)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)

    def forward(self, queries, keys, values, valid_lens):
        # queries[batch_size, 查询个数, query_size]
        # keys[batch_size, 键值对个数, key_size]
        # values[batch_size, 键值对个数, value_size]
        # valid_lens[batch_size,] 或者[batch_size, 查询个数]
        # 经过变换之后:[batch_size * num_heads, 查询/键值对个数, num_hiddens/num_heads]
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)
        if valid_lens is not None:
            valid_lens = torch.repeat_interleave(valid_lens, repeats=self.num_heads, dim=0)
        output = self.attention(queries, keys, values, valid_lens)
        # output[batch_size*num_heads, 查询个数, num_hiddens/num_heads]
        output_concat = transpose_output(output, self.num_heads)
        # 输出[batch_size, 查询个数, num_hiddens]
        return self.W_o(output_concat)

5. Layer Norm

说到Layer Norm就不得不比较它和Batch Norm的区别，Batch Norm是在batch那一个维度上做标准化，例如一个batch有n个句子，每个句子长度不一，如果做Batch Norm是对每句话的第一个字做一次，每句话的第二个字做一次，那么问题就来了，由于长度不一，如果这样做标准化肯定是不合理的，因为有的句子较短，做标准化时会缺失。而Layer Norm是每句话自己做标准化，所以这里采用了Layer Norm。代码如下：

class AddNorm(nn.Module):

    def __init__(self, normalization_shape, dropout, **kwargs):
        super(AddNorm, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)
        self.ln = nn.LayerNorm(normalization_shape)

    def forward(self, X, Y):
        return self.ln(self.dropout(Y) + X)

6. 前馈神经网络

简单来说就是一个线性层，做一个线性变换，代码如下:

class PositionWiseFFN(nn.Module):

    def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs, **kwargs):
        super(PositionWiseFFN, self).__init__(**kwargs)
        self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
        self.relu = nn.ReLU()
        self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)

    def forward(self, X):
        return self.dense2(self.relu(self.dense1(X)))

7. Transformer

万事俱备，现在就可以根据论文给的结构来搭建整体的结构了。

1. Encoder块

根据论文结构，Encoder由多头attention，add&Norm, 前馈神经网络组成，代码如下：

class EncoderBlock(nn.Module):

    def __init__(self, key_size, query_size, value_size,num_hiddens,
                 norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
                 dropout, use_bias=False, **kwargs):
        super(EncoderBlock, self).__init__(**kwargs)
        self.attention = MultiHeadAttention(key_size, query_size, value_size,
                                                num_hiddens, num_heads, dropout, use_bias)
        self.addnorm1 = AddNorm(norm_shape, dropout)
        self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens, num_hiddens)
        self.addnorm2 = AddNorm(norm_shape, dropout)

    def forward(self, X, valid_lens):
        Y = self.addnorm1(X, self.attention(X, X, X, valid_lens))
        return self.addnorm2(Y, self.ffn(Y))
        
X = torch.ones((2, 100, 24)) # [batch_size, seq_len, num_hiddens]
valid_lens = torch.tensor([3, 2])
encoder_blk = EncoderBlock(24, 24, 24, 24, [100, 24], 24, 48, 8, 0.5)
encoder_blk.eval()
encoder_blk(X, valid_lens).shape

输出为

torch.Size([2, 100, 24])

叠加任意多个编码器块并不会改变输出的形状，叠加Encoder块的代码如下：

class TransformerEncoder(nn.Module):

    def __init__(self, vocab_size, key_size, query_size, value_size,
                 num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
                 num_heads, num_layers, dropout, use_bias=False, **kwargs):
        super(TransformerEncoder, self).__init__(**kwargs)
        self.num_hiddens = num_hiddens
        self.embedding = nn.Embedding(vocab_size, num_hiddens)
        self.pos_encoding = PositionalEncoding(num_hiddens, dropout)
        self.blks = nn.Sequential()
        for i in range(num_layers):
            self.blks.add_module("block" + str(i),
                                 EncoderBlock(key_size, query_size, value_size, num_hiddens,
                                              norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
                                              dropout, use_bias))

    def forward(self, X, valid_lens, *args):
        X  = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
        # 由于位置编码采用的是三角函数编码，数值在-1到+1之间，而embedding之后的输入值往往很小，所以乘以根号维度可以把值放大到和位置编码差不多的数量级。
        self.attention_weights = [None] * len(self.blks)
        for i, blk in enumerate(self.blks):
            X = blk(X, valid_lens)
            self.attention_weights[i] = blk.attention.attention.attention_weights
        return X

2. Decoder块

解码器块和编码器略有区别，多了一个自己输入的attention，代码如下：

class DecoderBlock(nn.Module):

    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
                 dropout, i, **kwargs):
        super(DecoderBlock, self).__init__(**kwargs)
        self.i = i
        self.attention1 = MultiHeadAttention(key_size, query_size, value_size, num_hiddens, num_heads, dropout)
        # 解码器输入的注意力层
        self.addnorm1 = AddNorm(norm_shape, dropout)
        self.attention2 = MultiHeadAttention(key_size, query_size, value_size, num_hiddens, num_heads, dropout)
        # 和编码器的输出做注意力
        self.addnorm2 = AddNorm(norm_shape, dropout)
        self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens, num_hiddens)
        self.addnorm3 = AddNorm(norm_shape, dropout)

    def forward(self, X, state):
    	# state包括三个东西:编码器的输出,valid_lens,解码器输出的记录
    	# decoder的输入是基于每一次解码之后的输出
    	# 训练阶段时，一个句子的所有词元是一起输入，因此需要做遮蔽，比如第一个词看不到第二个词之后后面的词，第二个词看不到从第三个开始之后的词
    	# 预测阶段，由于是一个一个词元地输入，因此decoder只能看见当前词元之前的词，不需要做遮蔽
    	# X[batchsize, seq_len, num_hiddens]
        enc_outputs, enc_valid_lens = state[0], state[1]
        if state[2][self.i] is None:
            key_values = X
        else:
            key_values = torch.cat((state[2][self.i], X), axis=1)
        state[2][self.i] = key_values
        if self.training:
            batch_size, num_steps, _ = X.shape
            dec_valid_lens = torch.arange(1, num_steps+1, device=X.device).repeat(batch_size, 1)
        else:
            dec_valid_lens = None

        X2 = self.attention1(X, key_values, key_values, dec_valid_lens)
        Y = self.addnorm1(X, X2)
        Y2 = self.attention2(Y, enc_outputs, enc_outputs, enc_valid_lens)
        Z = self.addnorm2(Y, Y2)
        return self.addnorm3(Z, self.ffn(Z)), state

接着就可以将若干解码器块叠加到一起，代码如下：

class TransformerDecoder(nn.Module):

    def __init__(self, vocab_size, key_size, query_size, value_size,
                 num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
                 num_heads, num_layers, dropout, **kwargs):
        super(TransformerDecoder, self).__init__(**kwargs)
        self.num_hiddens = num_hiddens
        self.num_layers = num_layers
        self.embedding = nn.Embedding(vocab_size, num_hiddens)
        self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
        self.blks = nn.Sequential()
        for i in range(num_layers):
            self.blks.add_module("block"+str(i),
                                 DecoderBlock(key_size, query_size, value_size, num_hiddens,
                                              norm_shape, ffn_num_input, ffn_num_hiddens, num_heads, dropout, i))
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, enc_valid_lens, *args):
        return [enc_outputs, enc_valid_lens, [None] * self.num_layers]

    def forward(self, X, state):
        X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
        self._attention_weights = [[None] * len(self.blks) for _ in range (2)]
        for i, blk in enumerate(self.blks):
            X, state = blk(X, state)
            self._attention_weights[0][i] = blk.attention1.attention.attention_weights
            self._attention_weights[1][i] = blk.attention2.attention.attention_weights
        return self.dense(X), state

    @property
    def attention_weights(self):
        return self._attention_weights

3. 拼接编码器和解码器

class EncoderDecoder(nn.Module):
    
    def __init__(self, encoder, decoder, **kwargs):
        super(EncoderDecoder, self).__init__(**kwargs)
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, enc_X, dec_X, *args):
        enc_outputs = self.encoder(enc_X, *args)
        dec_state = self.decoder.init_state(enc_outputs, *args)
        return self.decoder(dec_X, dec_state)
encoder = TransformerEncoder(len(src_vocab), key_size, query_size, value_size, num_hiddens,norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
num_layers, dropout)

decoder = TransformerDecoder(len(tgt_vocab), key_size, query_size, value_size, num_hiddens,norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
num_layers, dropout)

net = d2l.EncoderDecoder(encoder, decoder)