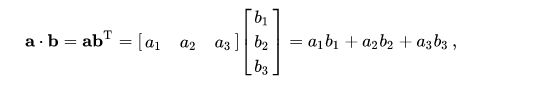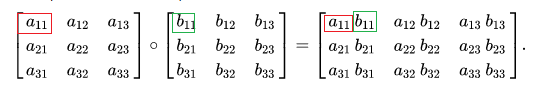Keras入门笔记(番一)：从源码分析K.batch_dot及与dot的区别

动机

矩阵和向量的乘法各种名称都有，甚至相互混杂，在不同框架里的命名也不一样，每每都会陷入这些Magic中。例如，同样是dot对向量shape= (n,)和一维张量shape=(n,1)而言都不一样，无论总结过多少次，像我们这种torch和tensowflow、matlab轮着写的人，总是不经意间就会翻车。

好在keras提供了高级的接口，至少在tensorflow、theano以及可能会有的mxnet上的表现是一致的。

各种向量乘法的命名

我个人非常烦什么“点积、外积、内积、点乘、叉乘、直积、向量积、张量积”的说法，乱的不行。我觉得，还是应该统一一下，别一会儿点积一会儿点乘，二维一维都不区分，非常容易乱。由于中文教材各种翻译都有，因此主要还是用wiki作为统一吧。

一维(向量)

• 需要注意的是，shape=(n, )的才是一维向量，shape(n,1)已经变成张量了。

1. Dot product
   

import numpy as np
a = np.array([1,2,3,4,5])  # 向量，不区分列向量或行向量。应该视为列向量。
b = a.reshape((5,1))  # 张量
print(a.shape, b.shape, a.T.shape)  # (5,) (5, 1) (5,)
print((a+b).shape)  # (5, 5)
print(np.dot(a,a), a*a)  # 55 [1 4 9 16 25]
print(np.dot(b.T,b))  # [[55]]
# Also, a*a = np.multiply(a, a), b*b = np.multiply(b, b)

2. Cross product

构建神经网络时基本不用，仅在工程优化中大量使用，如共轭梯度等。API一般为cross(a, b)。

3. element-wise

逐元素乘法，也就是 Dot product 不进行求和：$c_i=a_i{b}_i$。API一般为multiply(a, b)

二维(矩阵)

1. Hadamard product

常说的对应元素逐元素相乘。也是element-wise的一种。API一般是multiply(a, b)。

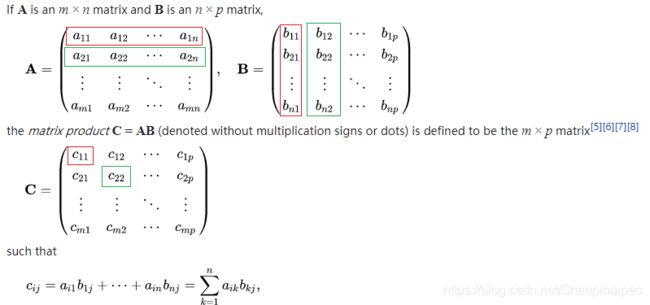
2. Matrix multiplication

就是线代中的矩阵乘法。一般也由dot(a, b)或matmul(a, b)实现。

三维以上(高维张量)

Tensor product

由于涉及到群和多重线性代数，Tensor product不是太好表示，看wiki即可。

简单区分dot与matmul

• keras.dot 实际上并不进行实际的计算，只是在matmul上加了一层封装，用于适配一维dot product和稀疏向量计算时的优化，对nD张量进行相乘的规则进行补充。直接读源码：

if ndim(x) is not None and (ndim(x) > 2 or ndim(y) > 2):
    # 对`nD`张量进行相乘的规则进行补充
    # 同时适配x y 维度不一致的情况
    # 即： x的最后一个维度与y的最后一个维度应当相同，这两个维度的元素进行dot product
    # 例如 a.shape = (5, 6) b.shape=(8, 6, 3) => dot(a,b).shape=(5, 8, 3)
    # 其在xy的最后两个维度上的表现，就如同二维Matrix multiplication一样。
    x_shape = []
    for i, s in zip(int_shape(x), tf.unstack(tf.shape(x))):
        if i is not None:
            x_shape.append(i)
        else:
            x_shape.append(s)
    x_shape = tuple(x_shape)
    y_shape = []
    for i, s in zip(int_shape(y), tf.unstack(tf.shape(y))):
        if i is not None:
            y_shape.append(i)
        else:
            y_shape.append(s)
    y_shape = tuple(y_shape)
    y_permute_dim = list(range(ndim(y)))
    y_permute_dim = [y_permute_dim.pop(-2)] + y_permute_dim
    xt = tf.reshape(x, [-1, x_shape[-1]])
    yt = tf.reshape(tf.transpose(y, perm=y_permute_dim), [y_shape[-2], -1])
    return tf.reshape(tf.matmul(xt, yt),
                      x_shape[:-1] + y_shape[:-2] + y_shape[-1:])
# 在2维和低维情况下
if is_sparse(x):
    out = tf.sparse_tensor_dense_matmul(x, y)
else:
    out = tf.matmul(x, y)
return out

keras.batch_dot函数源码分析

虽然这个函数中带有一个dot，然而其和dot没有太大关联。其更多的是一种可自定义维度的element-wise算法，注重的是对深度学习中的维度规则进行了优化：往往第一个维度是批样本的batch_size，非常适用于计算诸如${\sum }_i{a}_{ij}{b}_{j|i}$的场景。

源码分为两个部分，第一个部分：

    # axes 对应了x, y向量中分别准备进行dot product的维度
    if isinstance(axes, int):
        axes = (axes, axes)
    x_ndim = ndim(x)
    y_ndim = ndim(y)
    if axes is None:
        # behaves like tf.batch_matmul as default
        axes = [x_ndim - 1, y_ndim - 2]
    if py_any([isinstance(a, (list, tuple)) for a in axes]):
        raise ValueError('Multiple target dimensions are not supported. ' +
                         'Expected: None, int, (int, int), ' +
                         'Provided: ' + str(axes))
    #  将二者补齐维度，补为1维
    if x_ndim > y_ndim:
        diff = x_ndim - y_ndim
        y = tf.reshape(y, tf.concat([tf.shape(y), [1] * (diff)], axis=0))
    elif y_ndim > x_ndim:
        diff = y_ndim - x_ndim
        x = tf.reshape(x, tf.concat([tf.shape(x), [1] * (diff)], axis=0))
    else:
        diff = 0

接着是第二部分，主要涉及了补充了计算的逻辑：

    if ndim(x) == 2 and ndim(y) == 2:
        # 如果都是二维矩阵，则效果等同于直接计算二者矩阵乘积的对角线上的值
        # (实际上是 x y 进行hadamard product，然后在相应维度axes[0]、axes[1]上进行求和)
        if axes[0] == axes[1]:
            out = tf.reduce_sum(tf.multiply(x, y), axes[0])
        else:
            out = tf.reduce_sum(tf.multiply(tf.transpose(x, [1, 0]), y), axes[1])
    else:
       # 不都是二维矩阵的话，进行矩阵计算
        if axes is not None:
            # 判断是否要进行共轭和转置
            # 需要注意的是它并不对axes[0]的值进行传递而只是检测
            # 这是一个比较magic的诡点，所以axes[1, 1] 可能会和[1000, 1000]的结果是一样的
            adj_x = None if axes[0] == ndim(x) - 1 else True
            adj_y = True if axes[1] == ndim(y) - 1 else None
        else:
            adj_x = None
            adj_y = None
        # 这个计算比较精髓，涉及到线代知识。总之其效果是，给定的轴hadamard product然后求和
        # 同维度情况下，对最后两维进行矩阵乘法，axes不起作用
        out = tf.matmul(x, y, adjoint_a=adj_x, adjoint_b=adj_y)
    if diff:
        # 在不是同维矩阵的情况下，
        if x_ndim > y_ndim:
            idx = x_ndim + y_ndim - 3  # (x_ndim-1+y_ndim-1) -1 二者总维度的序-1
        else:
            idx = x_ndim - 1
        # x_ndim较大的情况下，多余的维度全部挤压，保证输出维度只有x_dim+y_dim-2
        # 否则输出维度为x_ndim
        out = tf.squeeze(out, list(range(idx, idx + diff)))
    if ndim(out) == 1:
        # 扩充维度以保证输出维度不为1
        out = expand_dims(out, 1)
    return out

坑：magic分析

对于所提到的magic，举一个例子：

a = K.ones([100, 10, 16, 5])
b = K.ones([100, 10, 16, 9])
with tf.Session() as sess:
    print(K.batch_dot(a, b, axes=[2, 2]).shape) # (100, 10, 5, 9)
    print(K.batch_dot(a, b, axes=[100, 1000]).shape) # (100, 10, 5, 9)
    # 分析以上结果
    #    1.axes[0]都非x最后一维，x共轭转置；
    #    2.axes[1]都非y最后一维，y不共轭转置。
    #    3.消掉最后一个相同的维度

另一段代码：

a = K.ones([100, 10, 16, 5])
b = K.ones([100, 10, 9, 16])
with tf.Session() as sess:
    print(K.batch_dot(a, b, axes=[2, 3]).shape)
    # 分析以上结果
    #    1.axes[0]不是x最后一维，x共轭转置；
    #    2.axes[1]是y最后一维，y共轭转置。
    #    3.消掉分别标注的维度