北京二手房价格预测

北京二手房价格预测

项目介绍

根据链家上的北京二手房信息，对数据进行进一步的清洗处理，分析各特征和价格之间的关系，筛选对价格影响比较显著的特征，探索北京二手房的价格情况，并建立房价预测模型

数据预处理

读取数据

#导入库
import numpy as np
import pandas as pd
import random
from datetime import datetime
from matplotlib import pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import Lasso
from sklearn.ensemble import RandomForestRegressor
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

df=pd.read_csv(r'D:\BI study download\lianjia\lianjia.csv')
df.head()

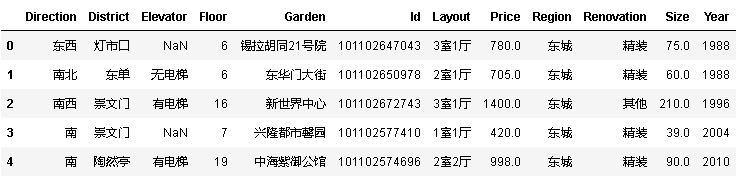
‘Direction’：房屋朝向
‘District’：房屋所在区域
‘Elevator’：电梯情况
‘Floor’：所在楼层
‘Garden’：所在楼盘
‘Id’：房屋id
‘Layout’：房屋房型
‘Price’：价格
‘Region’：所在行政区
‘Renovation’：装修情况
‘Size’：面积
‘Year’：所建年份

df.info()

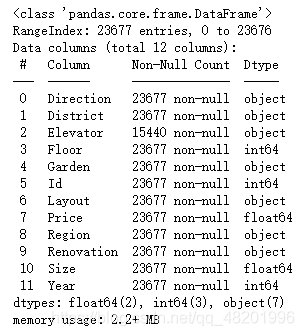
观察数据后发现，Elevator有大量空值，其属于分类变量，NAN代表无电梯，因此用无电梯替换内容

df['Elevator'].fillna('无电梯',inplace=True)

删除重复值

df.drop_duplicates(inplace=True)
df.reset_index(drop=True, inplace=True)

数据分析

区域和价格的关系

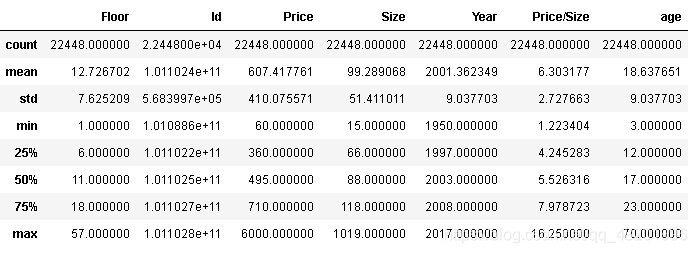
df.describe()

fig,ax = plt.subplots(1,2,figsize=(16,6))
data0.boxplot(column=['Price'], flierprops={'markeredgecolor':'red', 'markersize':4}, ax=ax[0])
data0.boxplot(column=['Size'], flierprops={'markeredgecolor':'red', 'markersize':4}, ax=ax[1])

经观察数据，北京二手房的面积大概率集中在15-200平米，价格集中在60-1200万。价格最低的二手房为60万，最高6000万；面积最小为15平米，最大为1019平米。北京一套二手房的平均价格为607万，平均面积99平米。
本次分析中，为减少价格极高的二手房对整体数据的影响，只考虑大部分人可以承担的二手房价格，放弃价格属于异常值得数据，即价格超过1200的二手房数据作为异常值删除。¶

df.drop(index = df[df['Price'] > 1200].index, inplace=True)
df.info()

可视化不同地区的房屋价格和数量

fig,ax = plt.subplots(2,1,figsize=(30,18))
x = data0['Region'].unique()

y0 = data0.groupby(by=['Region']).size().sort_values(ascending=False)
sns.barplot(x,y0,ax=ax[0],palette='Reds_d')
ax[0].set_title('北京各区二手房在售数量')

y1 = data0.groupby(by=['Region'])['Price'].mean().sort_values(ascending=False)
sns.barplot(x,y1,ax=ax[1],palette='Blues_r')
ax[1].set_title('北京各区二手房在售均价')

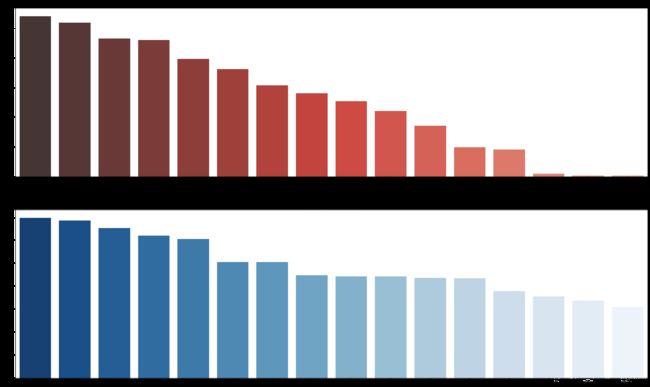
北京二手房的分布，东城区最多，其次是西城和朝阳，石景山最少。房价的分布和二手房数量的分布保持一致，也是东城区到石景山从高到低排序。
说明二手房市场价格高的区，房屋供给数量也多。高价地区的房屋均值和和低价地区的价格均值差值较大，说明房屋所在区是影响房间的重要因素。

朝向和价格的关系

plt.figure(figsize=(30,8))
x = df['Direction'].unique()

y = df.groupby(by=['Direction'])['Price'].mean().sort_values(ascending=False)
x1=x[:20]
y1=y[:20]
sns.barplot(x1,y1,palette='Greens_r')

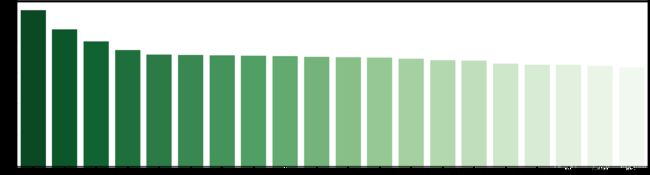
南北朝向的二手房的平均价格最高，符合人们挑选房屋时的喜好，因为南北朝向的房屋采光好,但对价格影响相对不大。

装修和价格关系

plt.figure(figsize=(20,8))
x = df['Renovation'].unique()

y = df.groupby(by=['Renovation'])['Price'].mean().sort_values(ascending=False)
sns.barplot(x[:4],y[:4],palette='Reds_r')

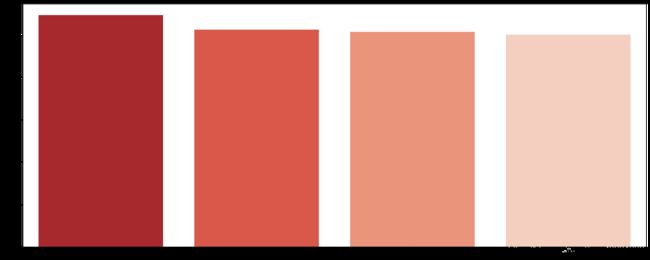
精装修的二手房价格最高，符合市场规律。而简装和毛坯方的价格十分接近。但影响也不大。

年龄和价格的关系

fig,ax = plt.subplots(2,1,figsize=(30,18))
x = df['age'].unique()

y0 = df.groupby(by=['age']).size().sort_values(ascending=False)
sns.barplot(x,y0,ax=ax[0],palette='Reds_d')
ax[0].set_title('北京各房龄二手房在售数量')

y1 = df.groupby(by=['age'])['Price'].mean().sort_values(ascending=False)
sns.barplot(x,y1,ax=ax[1],palette='Blues_r')
ax[1].set_title('北京各房龄二手房在售均价')

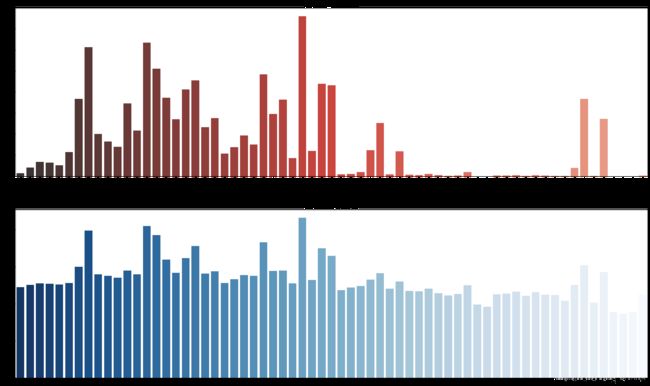
北京二手房市场中的二手房的房龄大部分集中在10-35年，几年新的二手房出售数量较少；
在房屋价格上，几年新的二手房平均价格反而没有10年以上的高。
北京60年以上的老房子也有相对较多出售，而且其价格也不低。¶

房型和价格的关系

#数量和户型的关系
plt.figure(figsize=(20,8))
x = df['Layout'].unique()
print(x)
y = df.groupby(by=['Layout']).size().sort_values(ascending=False)
sns.barplot(x[:10],y[:10],palette='Oranges'

plt.figure(figsize=(20,8))
x = df['Layout'].unique()

y = df.groupby(by=['Layout'])['Price'].mean().sort_values(ascending=False)
sns.barplot(x[:10],y[:10],palette='YlGn')

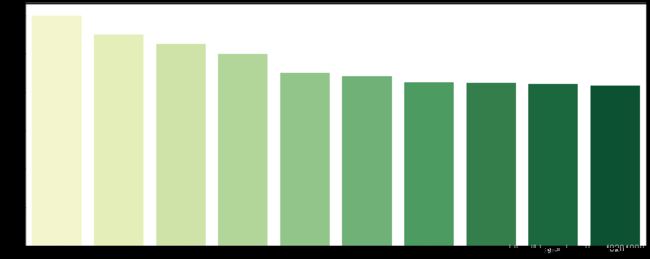
北京二手方市场上的房型众多，其中数量最多的是3室1厅的房型，其次是2室1厅。
1室1厅和2室2厅数量接近，而0厅房型的二手房的数量也在前几名。
价格分布基本和房型数量保持一致，说明市场需求大部分集中在3室1厅，2室1厅，1室1厅和2室2厅房型。各房型之间价格有差距，但是差值较小，说明其对价格的影响相对较小。¶

相关性分析

删除无用数据

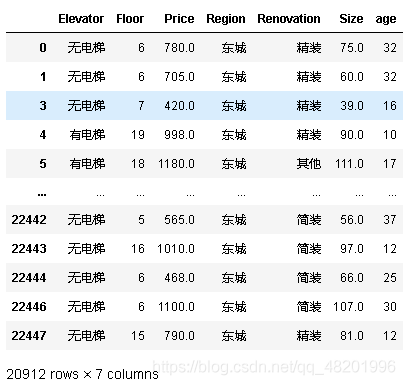
df1=df.dropna()
df1.drop(columns=['District','Garden','Id','Year','Direction','Layout'],inplace=True)
df1

df['Renovation'] = df['Renovation'].map({'毛坯':0,'简装':1,'精装':2,'其他':3})
df['Elevator'] = df['Elevator'].map({'无电梯':0,'有电梯':1})
map1 = {'东城':13, '西城':12, '朝阳':11, '海淀':10, '丰台':9, '昌平':8, '大兴':7, '房山':6, '门头沟':5, '顺义':4,
       '亦庄开发区':3, '通州':2, '石景山':1}
df1['Region'] = df1['Region'].map(map1)

df.corr()[['Price']]

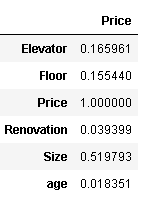
根据和价格的相关系系数可以看出，面积和价格的关系最大，房屋年龄、有无电梯、楼层的影响较小，
装修方式影响最小。

数据建模

# 分割x，y
x = df.drop(columns=['Price'])
y = df['Price']
x_train, x_test, y_train, y_test = train_test_split(x, y,train_size=0.7)

#训练模型
#决策树
dt = DecisionTreeRegressor(max_depth = 9)
dt.fit(x_train,y_train)
print(round(dt.score(x_train,y_train),2))
print(round(dt.score(x_test,y_test),2))

训练集得分：0.83
测试集得分：0.76

#随机森林
rf = RandomForestRegressor()
rf.fit(x_train,y_train)
print(f'训练集得分：{round(rf.score(x_train,y_train),2)}')
print(f'测试集得分：{round(rf.score(x_test,y_test),2)}')

训练集得分：0.97
测试集得分：0.81

模型评估

from sklearn.metrics import mean_squared_error,explained_variance_score,mean_absolute_error,r2_score
y_dt_train_pred=dt.predict(x_train)
y_dt_test_pred=dt.predict(x_test)
print ("决策树模型评估--训练集：")
print ('训练r^2:',dt2.score(x_train,y_train))
print ('均方差',mean_squared_error(y_train,y_dt_train_pred))
print ('绝对差',mean_absolute_error(y_train,y_dt_train_pred))
print ('解释度',explained_variance_score(y_train,y_dt_train_pred))

print ("决策树模型评估--验证集：")
print ('验证r^2:',dt2.score(x_test,y_test))
print ('均方差',mean_squared_error(y_test,y_dt_test_pred))
print ('绝对差',mean_absolute_error(y_test,y_dt_test_pred))
print ('解释度',explained_variance_score(y_test,y_dt_test_pred))

决策树模型评估–训练集：
训练r^2: 0.8294930763481481
均方差 8860.336245868666
绝对差 67.93515170770496
解释度 0.8294930763481481
决策树模型评估–验证集：
验证r^2: 0.7609894681294798
均方差 12372.514039142869
绝对差 80.04623630560512
解释度 0.7610291620178595

from sklearn.metrics import mean_squared_error,explained_variance_score,mean_absolute_error,r2_score
y_rf_train_pred=rf.predict(x_train)
y_rf_test_pred=rf.predict(x_test)
print ("随机森林模型评估--训练集：")
print ('训练r^2:',rf.score(x_train,y_train))
print ('均方差',mean_squared_error(y_train,y_rf_train_pred))
print ('绝对差',mean_absolute_error(y_train,y_rf_train_pred))
print ('解释度',explained_variance_score(y_train,y_rf_train_pred))

print ("决策树模型评估--验证集：")
print ('验证r^2:',rf.score(x_test,y_test))
print ('均方差',mean_squared_error(y_test,y_rf_test_pred))
print ('绝对差',mean_absolute_error(y_test,y_rf_test_pred))
print ('解释度',explained_variance_score(y_test,y_rf_test_pred))

随机森林模型评估–训练集：
训练r^2: 0.971018612989481
均方差 1506.0082504870181
绝对差 25.9558480075792
解释度 0.9710206214565889
决策树模型评估–验证集：
验证r^2: 0.8149524957794424
均方差 9579.087691070848
绝对差 67.22141777497437
解释度 0.8149560221079576

随机森林模型训练集得分（0.97）和测试集（0.81）得分都高于决策树模型，并且随机森林的均方误差和平均绝对误差都小于决策树。因此随机森林的拟合更好。

实例模拟

一名用户想在二手房市场上出售一套二手房，他的房子情况如下：有电梯（1），6层（6），东城区（13），精装（2），面积100平米（100），房龄20（20），预测其在该数据集统计年份时可在市场上的售价。

apply = np.array([1,6,13,2,100,20]).reshape(1,-1)
#poly_apply = poly.fit_transform(apply)
round(rf.predict(apply)[0],2)

894.66
预测该房屋的价格为894.66万元