概述:隐式神经表示(Implicit Neural Representations,INRs)
隐式神经表示(Implicit Neural Representations,INRs)
- 1 简介
-
- 1.1 传统的隐式表示
-
- 1.1.1 代数表示
- 1.1.2 函数表示
- 1.1.3 水平集表示(level set)
- 1.2 什么是隐式神经表示
- 1.3 隐式神经表示的优缺点
-
- 1.3.1 优点
- 1.3.2 缺点
- 2 应用
-
- 2.1 超分辨率
- 2.2 新视角合成
- 2.3 三维重建
- 3 隐式神经表示的结构及改进
-
- 3.1 隐式神经表示常用的网络结构
- 3.2 隐式神经表示的改进
-
- 3.2.1 SIREN
- 3.2.2 FPE
- 引用
1 简介
1.1 传统的隐式表示
传统用于形状表示的隐式表示有:代数表示、函数表示、水平集表示等。
1.1.1 代数表示
如下图利用对基础图形的交并补,可以得到复杂的图形。一般logo的设计或者三维零部件建模都是利用对基础图形的布尔运算来得到目标形状。


1.1.2 函数表示
除了代数以外,还可以用一些解析的函数来表示形状。简单的就是圆以及椭圆的函数表达式。Rhodin等人将三维人体近似为高斯密度场,利用91个高斯函数去逼近出人体轮廓。除此之外,符号距离函数也常用来表示三维形状,如图通过提取零值点可以将三维模型表面提取出来。


1.1.3 水平集表示(level set)
一些形状是无法解析表示出来的,但是可以通过设定的水平集提取出形状。例如在医学中的CT、MRI,根据组织密度以及设定的水平集,就可以重构组织的三维体积模型。

1.2 什么是隐式神经表示
隐式神经表示(Implicit Neural Representation,INR)(有时也称为基于坐标的表示)是一种对各种信号进行参数化的新方法。传统的信号表示通常是离散的,而隐式神经表示将信号参数化为一个连续函数,将信号的域映射到该坐标上的属性的值(例如对于图像,就是将像素坐标映射到R,G,B颜色)。
![]()
当然,这些函数通常不是解析性的——即不可能“写下”将自然图像参数化为数学公式的函数。隐式神经表示通过神经网络来近似信号函数。
1.3 隐式神经表示的优缺点
1.3.1 优点
- 表示不再与空间分辨率相耦合,例如,图像与像素数量相耦合的方式。隐式神经表示是连续函数,因此参数化信号所需的内存与空间分辨率无关,只与底层信号的复杂性相关。另一个推论是,隐式表示具有“无限分辨率”——它们可以在任意空间分辨率下进行采样。所以隐式表示解决了在显示表示中显存的限制,使得高/超分辨率成为可能。
- 表征能力更强,跨神经隐式表示的泛化等同于学习函数空间上的先验,通过学习神经网络权重上的先验实现。学习后的隐式神经表示可以通过不同的坐标输入映射到任意属性值。
- 泛化性高,神经隐式表示学习函数空间上的先验,然后根据提取的先验以及输入的特征,可以得到不同的目标信号。
- 易于学习,基于神经网络的隐式神经表示易于与各种网络结构结合,能够快速的学习先验,拟合学习对象。与传统的表示形式(如网格、点云或体素)相比,神经隐式表征可以灵活地融合到可微分的基于学习的管道中。
1.3.2 缺点
- 需要后处理:显示几何必须通过一定的后处理步骤得到,往往这也是非常耗时的。
- 过度平滑:全连接的网络结构以及全局条件(特征)都容易导致过度平滑。
- 难以实时:隐式神经表示需要对整个volume的体素的函数值进行计算,计算量大,十分耗时。
2 应用
隐式神经表示,在表示各种复杂信号都得到了广泛应用,这里举三个应用:超分辨率、新视角合成、三维重建。
2.1 超分辨率
2.2 新视角合成
2.3 三维重建
3 隐式神经表示的结构及改进
从2.3的可以看出重建的模型是比较平滑的,缺乏细节的信息,那么是什么导致了这个原因呢?接下来就来看一下隐式神经表示常用的网络结构吧!
3.1 隐式神经表示常用的网络结构
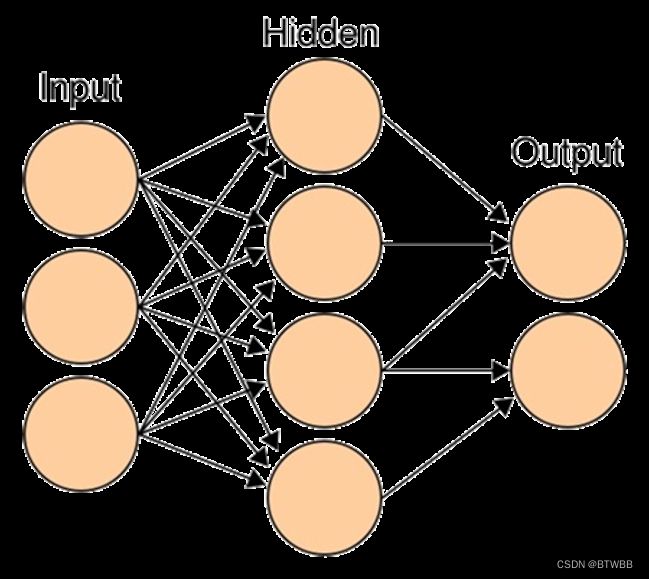
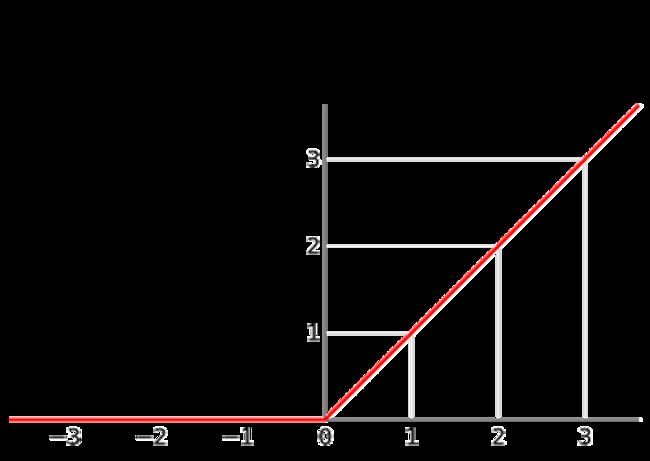
基于ReLU的多层感知器(MLP)是隐式神经表示常用的网络结构。Hornik[1]在1989年证明,当中间隐含层的神经元数量趋于无穷多时,多层感知机可以拟合任何非线性函数。
3.2 隐式神经表示的改进
3.2.1 SIREN
SIREN[2]:在隐形神经表示中使用了正弦函数来替代以往的激活函数,即将多层感知器(mlp)中线性整流函数替代为周期性正弦函数。
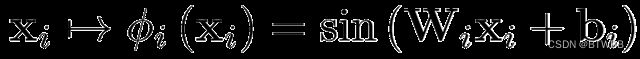

SIREN比ReLU-MLP更好地表示信号中的细节,证明了其在表示复杂的自然信号(如图像\视频\音频\三维形状)及其导数的优势。
3.2.2 FPE
MLP总是倾向于学习更光滑的结果,而对高频信号的刻画差强人意。造成这种现象的原因是网络自身的频谱偏置,使其更容易学习低频部分而忽略高频部分(换句话来说就是高频信号的在目标函数特征值小,故而在每次参数更新中受到的惩罚小,收敛很慢很慢,甚至几乎学不出来。)。2020Tancik 等人[3]提出了一个新的方法FPE(傅里叶位置编码)而这篇文章则在讲要怎么克服网络的频谱偏置。它提出了一种将网络input从低维映射到高维的一种方式,让MLP在不增加容量的情况下也能够学好高频信号,具体是通过一个简单的傅立叶特征映射来传递输入点,使多层感知器(MLP)可以学习低维问题域中的高频函数。

用多层感知机网络去学习表示图像,可以看到在图像的表示上加入位置编码后图像的细节信息明显被更多的保留了下来,并且高频的细节信息得到了更快的收敛。
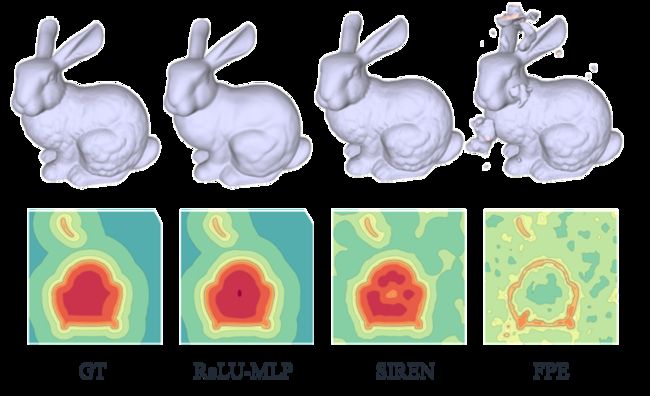
但是如上图所示其也存在一定的问题,低频分类不能被很好地拟合,从而会导致结果带有较多的噪声、瑕疵。
其它隐式神经表示相关改进的论文可查阅“神经表示(INRs)相关论文汇总”。
引用
本文的大部分图片来自百度!
[1] Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators[J]. Neural networks, 1989, 2(5): 359-366.
[2] Sitzmann V, Martel J, Bergman A, et al. Implicit neural representations with periodic activation functions[J]. Advances in Neural Information Processing Systems, 2020, 33: 7462-7473.
[3] Tancik M, Srinivasan P, Mildenhall B, et al. Fourier features let networks learn high frequency functions in low dimensional domains[J]. Advances in Neural Information Processing Systems, 2020, 33: 7537-7547.


