TensorFlow 学习笔记-5
TensorFlow优化器
前置知识
损失函数
概念
损失函数是评估特定模型参数和特定输入时,表达模型输出的推理值与真实值之间不一致程度
的函数。损失函数L的形式化定义如下:
l o s s = L ( f ( x i ; θ ) , y i ) loss=L(f(x_i;θ),y_i) loss=L(f(xi;θ),yi)
常见的损失函数有平方损失函数、交叉熵损失函数和指数损失函数:
l o s s = ( y i − f ( x i ; θ ) ) 2 l o s s = y i ∗ l o g ( f ( x i ; θ ) ) l o s s = e x p ( − y i ∗ f ( x i ; θ ) ) loss=(y_i - f(x_i;θ))^2\\ loss=y_i*log(f(x_i;θ))\\ loss=exp(-y_i*f(x_i;θ)) loss=(yi−f(xi;θ))2loss=yi∗log(f(xi;θ))loss=exp(−yi∗f(xi;θ))
经验风险
使用损失函数对所有训练样本求损失值,再累加求平均可得到模型的经验风险。
换句话说,关于任务的表示函数f(x)关于训练集的平均损失就是经验风险,其形式化定义如下:
R e m p ( f ) = 1 N ∑ i = 1 N L ( f ( x i ; θ ) , y i ) R_{emp}(f) = \frac{1}{N}\sum_{i=1}^{N}L(f(x_i;θ),y_i) Remp(f)=N1i=1∑NL(f(xi;θ),yi)
然而,如果过度地追求训练数据上的低损失值,就会遇到过拟合问题。所以不要过分的追求低的损失值,训练集通常并不能完全代表真实场景的数据分布。当两者的分布不一致时,如果过分依赖训练集上的数据,面对新数据时就会无所适从,这时模型的泛化能力就会变差。在处理经验风险时,设置合理的阈值。
加入正则化项
模型训练的目标是不断最小化经验风险。随着训练步数的增加,经验风险将逐渐降低,模型复
杂度也将逐渐上升。为了降低过度训练可能造成的过拟合风险,可以引入专门用来度量模型复
杂度的正则化项(regularizer)或惩罚项( penalty term) J ( θ ) J(\theta) J(θ)。
常用的正则化项有L0、L1和L2范数。λ因此,我们将模型最优化的目标替换为鲁棒性更好的结构风险最小化(structural risk minimization, SRM)。如下所示,它由经验风险项和正则项两部分构成:
R s r m ( f ) = m i n 1 N ∑ i = 1 N L ( f ( x i ; θ ) , y i ) + λ J ( θ ) R_{srm}(f) = min\frac{1}{N}\sum_{i=1}^{N}L(f(x_i;θ),y_i)+\lambda J(\theta) Rsrm(f)=minN1i=1∑NL(f(xi;θ),yi)+λJ(θ)
在模型训练过程中,结构风险不断地降低。当小于我们设置的损失值阈值时,则认为此时的模
型已经满足需求。因此,模型训练的本质就是在最小化结构风险的同时取得最优的模型参数。
最优模型参数的形式化定义如下:
θ ∗ = a r g m i n θ R s r m ( f ) = a r g m i n θ 1 N ∑ i = 1 N L ( f ( x i ; θ ) , y i ) + λ J ( θ ) \theta ^* = arg\:min_θ\,R_{srm}(f) = arg\,min_\theta \frac{1}{N}\sum_{i=1}^{N}L(f(x_i;θ),y_i)+\lambda J(\theta) θ∗=argminθRsrm(f)=argminθN1i=1∑NL(f(xi;θ),yi)+λJ(θ)
优化算法
典型的机器学习和深度学习问题通常都需要转换为最优化问题进行求解。
求解最优化问题的算法称为优化算法,它们通常采用迭代求解方式实现:
首先设定一个初始的可行解,然后基于特定的函数(就是模型)反复重新计算可行解,直到找到—个最优解或达到预设的收敛条件。(神经网络本身就是一个函数,网络结构既定(给定函数))
不同的优化算法采用的迭代策略各有不同:
- 有的使用目标函数的一阶导数,如梯度下降法;
- 有的使用目标函数的二阶导数,如牛顿法、海森矩阵;
- 有的使用前几轮迭代的信息,如Adam。
典型的机器学习和深度学习问题,包含以下3个部分
-
模型: y = f ( x ) = W x + b y=f(x)=Wx+b y=f(x)=Wx+b,其中x是输入数据,y是模型输出的推理值,w和b是模型参数,即用户的训练对象。
-
损失函数: l o s s = L ( y , y ^ ) loss=L(y,\hat y) loss=L(y,y^),其中 y ^ \hat y y^是x对应的真实值(标签),loss为损失函数输出的损失值。
-
优化算法: w = w + a ∗ g r a d ( w ) , b = b + a ∗ g r a d ( b ) w=w+a*grad(w), b=b+a*grad(b) w=w+a∗grad(w),b=b+a∗grad(b),其中 g r a d ( w ) grad(w) grad(w)和 g r a d ( b ) grad(b) grad(b)分别表示当损失值为
loss时模型参数w和b各自的梯度值,a为学习率。
函数到底是长什么样?
那对于传统的机器学习,可能只需要确定函数线性的还是非线性、维度,函数表达式可以显式的写出来。但是对于深度神经网络,是很难显式的去写出表达式。更多的时候不知道它到底是一个什么样的函数,整个训练过程的函数,在训练过程当中是不断变化的一个东西,很难写出来它的这个表达式。
那这个时候呢只需要把它网络结构(按什么顺序,执行什么函数。即按什么流程,设计哪些节点 )确定下来就行,那第一部分我们把 y = f ( x ) y=f(x) y=f(x)把这个函数首先确定下来,然后定义损失函数,最小化我们的结构风险(得到局部最优的一个模型参数)(在实际的运行过程当中,可以用真实数据场景里的数据去不断的去优化算法)的。优化算法可以由优化器来实现。
优化器
优化器是实现优化算法的载体。
一次典型的迭代优化应该分为以下3个步骤:
- 计算梯度:调用compute_gradients方法;
- 处理梯度:用户按照自己需求处理梯度值,如梯度裁剪和梯度加权等;
- 应用梯度:调用apply_gradients方法,将处理后的梯度值应用到模型参数。
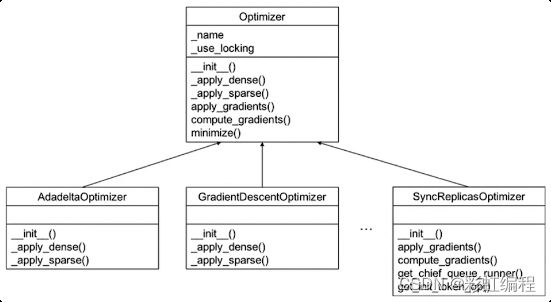
优化器的一个典型实现的继承关系
TensorFlow 的 Optimizer 基类中实现了这3个方法:apply_gradients()、compute_gradients()、minimize()
minimize()最小化目标函数,minimize内部其实就是调用了apply_gradients()、compute_gradients()
AdadeltaOptimizer
那么它内置的其他的实现好的优化器,都是继承的Optimizer的基类,实现这些方法的同时,也会实现对于张量和稀疏张量的这种不同数据类型的解决方法。
也有针对分布式训练的优化器SyncReplicasOptimizer:分布式结构梯度和分布式更新,这个模型参数的一个方法,里面就涉及到队列和比较复杂的更新操作
这里就不再展开
那这里可以看到
我们通过这个优化器去这个训练
我们模型参数的一个典型步骤
# 1.计算梯度
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
grads_and_vars = optimizer.compute_gradients(loss,var_list,...)
# 2.处理梯度
clip_grads_and_vars = [(tf.clip_by_value(grad,-1.0,1.0),var) for grad,var in grads_and_vars]
# 3.应用梯度
train_op = optimizer.apply_gradients(clip_grads_and_vars)
模式 2:直接通过minimize
# 计算并应用梯度到模型参数
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
global_step = tf.Variable(0,name='global_step',trainable=False)
train_op = optimizer.minimize(loss,global_step=global_step)
单步训练的最后的操作,涵盖了我们那张数据流图里面整个的逻辑
当你去用会话去执行train_op的时候,其实你就是在执行整个数据流图。不过TensorFlow核心运行时,会去帮你自动的找出你想要表达的这张数据流图里面的计算逻辑关系,然后依序的执行下去,而不会出现一些这个依赖问题。
TensorFlow 内部的一些优化器
TensorFlow内置的一些优化器以及对应的文件路径