Faster Read: LapSRN:Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution
Deep Laplacian Pyramid Networks CVPR2017
keywords: CNN(Convolutional Neural Network), Laplacian Pyramid,Super-Resolution
论文名称:
LapSRN:Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution
期刊(Fast and Accurate Image Super-Resolution with Deep Laplacian Pyramid Networks)
Prerequisite:Convolutional Neural Network, Laplacian Pyramid
目的:用拉普拉斯金字塔式的CNN结构做超分辨率。
重点:
- 将拉普拉斯金字塔的结构融入到CNN结构当中,仅用一种神经网络结构就训练出log2S层的超分辨率。比如,如果输入图片大小是32x32。如果想训练处输出为256x256的图像就需要3层。同时64x64,128x128的超分辨率图像也在过程中被创造出来。
- 采用了新的loss function。作者将从低分辨率(LR)到高分辨率(HR)的过程看做是方程的一对多的问题。而L2不能很好的突出这一点,所以自创了robust Charbonnier penalty function。
- 分析了应对vanish gradient的三种方法。
- 其他的细节和结果分析看论文。
==================================================================================
下面是部分重点的细节介绍,上面看懂的不用再往下看了。
==================================================================================
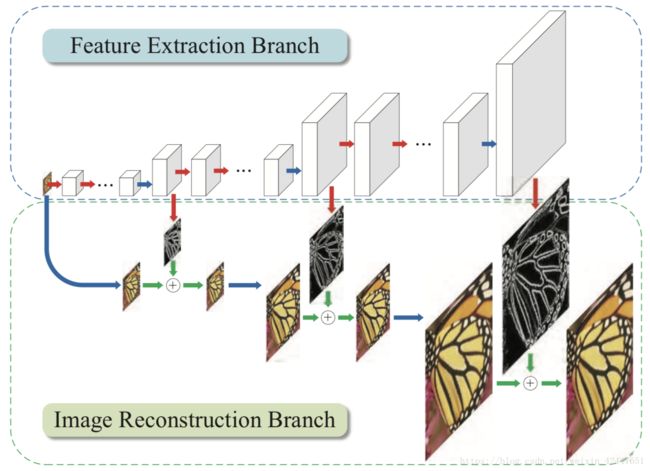
训练细节图:
为了减小计算压力,作者用了在层内和跨层的share parameter的方法。
为了应对vanish gradient的问题,作者用了三种类似在ResNet中使用过的skipping connection的方法。很显然,如果将输入图片以特定的方式贴入训练的中间层,那么gradient就不会很快消失。
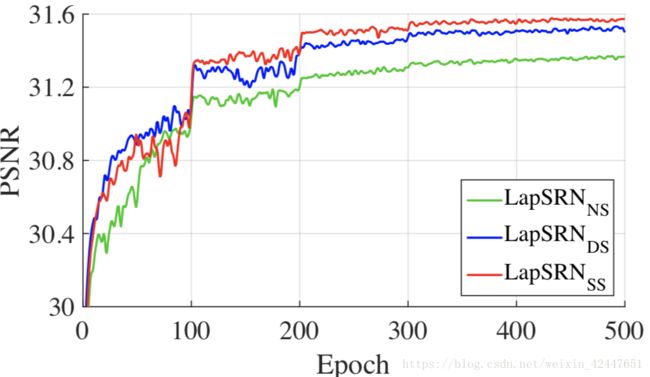
对于上述三种方法,作者从performance的角度做出了分析,结果ss要略高一点,ss就是Shared-source的缩写。
Loss function:
再提这个之前简单提一下常用的loss function。一般训练图片到图片的常用的是L2 func算loss。有L2就应该有L1。他俩分别叫:L1= Least Absolute Deviations
L2= Least Square Errors
两个方程如下:
方程很简单,就是做差。取label图像减去训练结果图像。L1取差的绝对值,L2取差的平方。
两者最主要的区别在于L2更加注重整体像素值的平均性。比如一个很小的图像,只有4个像素,他们是x1,x2,x3,x4.
如果四个差值分别是1, 1, 1, 1的话,那么结果L1 = L2 = 4。
L1 = |1| + |1| + |1| + |1| = 4
L2 = 1^2 + 1^2 + 1^2 + 1^2 = 4
但是,如果四个差是4, 0, 0, 0的话,L1还是4,L2就变成16了。也就是说pixel-wise的差值分布不均的话会被L2放大。那么back propagate之后,由于结果训练的结果是要减小loss的,所以像素值会趋近于平均。
那么趋近于平均的更新方法就带来了问题。如果把从LR到HR看做是一个方程f(x)的话,那么这个方程的自变量和因变量一定是一对多的关系。每一种loss function会使差值趋近于一种风格,比如L2就会把像素值拉平均。均匀分布的像素值可以理解为梯度适当的减小,所以会产生像高斯滤镜一样的模糊。而下面这个Charbonnier loss function一定是有针对性的。具体怎么有针对性,看论文Two deterministic half-quadratic regularization algorithms for computed imaging#xhe_tmpurl 我用不着,所以没看。
Ref:
CSDN: shwan_ma - https://blog.csdn.net/shwan_ma/article/details/78690974
Charbonnier - http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.469.129&rep=rep1&type=pdf
项目主页 - http://vllab.ucmerced.edu/wlai24/LapSRN/
论文期刊 - https://arxiv.org/abs/1710.01992
论文会议 - http://vllab.ucmerced.edu/wlai24/LapSRN/papers/cvpr17_LapSRN.pdf