密度峰值聚类算法(DPC)
目录
- 前言
- 一、DPC算法
-
- 1.1 DPC算法的两个假设
- 1.2 DPC算法的两个重要概念
- 1.3 DPC算法的执行步骤
- 1.4 DPC算法的优缺点
- 二、改进的DPC算法及其论文
-
- 2.1 局部密度和相对距离的定义
- 2.2 截断距离的调整
- 2.3 聚类中心的获取方法
- 2.4 制定新的分配规则
- 2.5 改进距离矩阵
- 三、聚类效果及其MATLAB代码
- 参考文献
前言
Rodriguez 等于2014年提出快速搜索和寻找密度峰值的聚类(clustering by fast search and find of density peaks),简称密度峰值聚类(density peaks clustering,DPC)算法。
一、DPC算法
1.1 DPC算法的两个假设
1)类簇中心被类簇中其他密度较低的数据点包围;
2)类簇中心间的距离相对较远。
1.2 DPC算法的两个重要概念
1)局部密度
设有数据集为 ,其中 ,N为样本个数,M为样本维数。
对于样本点i的局部密度,局部密度有两种计算方式,离散值采用截断核的计算方式,连续值则用高斯核的计算方式。
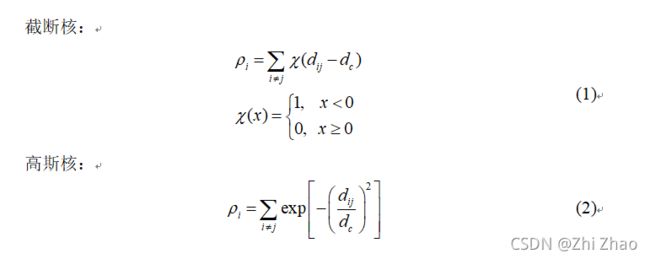
式中, d i j d_{ij} dij 为数据点 i i i 与数据点 j j j 的欧氏距离, d c d_{c} dc 为数据点i的邻域截断距离。
采用截断核计算的局部密度 ρ i ρ_{i} ρi 等于分布在样本点 i i i 的邻域截断距离范围内的样本点个数;而利用高斯计算的局部密度 ρ i ρ_{i} ρi 等于所有样本点到样本点i的高斯距离之和。
DPC算法的原论文指出,对于较大规模的数据集,截断核的计算方式聚类效果较好;而对于小规模数据集,高斯核的计算方式聚类效果更为明显。
2)相对距离
相对距离 δ i δ_{i} δi 指样本点 i i i 与其他密度更高的点之间的最小距离。在计算样本点 i i i 前需要对每个数据点的局部密度进行排序。
对于密度最高的样本,相对距离定义为:
δ i = m a x i ≠ j ( d i j ) δ_{i}=\underset{i≠j}{max}(d_{ij}) δi=i=jmax(dij)
对于其余数据点,相对距离定义为:
δ i = m i n j : ρ j > ρ i ( d i j ) δ_{i}=\underset{j:ρ_{j}>ρ_{i}}{min}(d_{ij}) δi=j:ρj>ρimin(dij)
由于密度最高的样本不存在比其密度更高的点,DPC认为该点必为密度峰值(类簇中心),人为设定其相对距离为最大值。剩余的密度峰值需要同时满足两个条件:局部密度 ρ ρ ρ 较高,相对距离 δ δ δ 较大。为此,DPC算法的原论文通过决策值 γ γ γ 寻找这类密度峰值,下式给出了 γ i γ_{i} γi 的定义:
γ i = ρ i × δ i γ_{i}=ρ_{i}×δ_{i} γi=ρi×δi
找到密度峰值后,DPC将剩余数据点分配给密度比它高的最近数据点所在类簇,形成多个从密度峰值出发的树状结构,每一个树状结构代表一个类簇。
1.3 DPC算法的执行步骤
1)利用样本集数据计算距离矩阵 d i j d_{ij} dij ;
2)确定邻域截断距离 d c d_{c} dc ;
3)计算局部密度 ρ i ρ_{i} ρi 和相对距离 δ i δ_{i} δi ;
4)绘制决策图,选取聚类中心点;
5)对非聚类中心数据点进行归类,聚类结束。
最后可以将每个簇中的数据点进一步分为核心点和边缘点两个部分,并检测噪声点。其中,核心点是类簇核心部分,其 ρ ρ ρ 值较大;边缘点位于类簇的边界区域且 ρ ρ ρ 值较小,两者的区分界定则是借助于边界区域的平均局部密度。
1.4 DPC算法的优缺点
优点:
1)不需要事先指定类簇数;
2)能够发现非球形类簇;
3)只有一个参数需要预先取值。
缺点:
1)当类簇间的数据密集程度差异较大时,DPC算法并不能获得较好的聚类效果;
2)DPC算法的样本分配策略存在分配连带错误。
二、改进的DPC算法及其论文
2.1 局部密度和相对距离的定义
- 引入k近邻(KNN)思想计算局部密度。当样本类簇密集程度相差较大时,全局范围内密度较高的点可能均存在于密集类簇中,这将难以发现正确的密度峰值;另外,每个类簇中的密度峰值,它的密度是所在类簇中密度较高的样本,即局部范围内密度较高的样本。因此,样本与其近邻点的相对密度可更加准确地反映该样本是否能成为类簇中心[1]。
- 引入共享近邻(SNN)思想计算局部密度和相对距离。前者通过计算两个点之间的共享邻居的数量快速准确地识别和分配肯定属于一个集群的点;后者通过查找更多邻居所属的簇来分配剩余的点。
2.2 截断距离的调整
- 针对截断距离参数的确定问题,构造关于截断距离参数的局部密度信息熵,通过最小化信息熵自适应地确定截断距离参数[3]。
- 寻找使基尼系数取得最小值时所对应的截断距离,并且将优化后的截断距离作为下一步聚类的基础,代替人工选取截断距离[4]。
- 建立以ACC指标为目标函数的优化问题,利用鲸鱼优化算法对目标函数进行优化,寻找最佳的截断距离[5]。
2.3 聚类中心的获取方法
- 针对聚类中心的确定问题,利用从非聚类中心到聚类中心数据点局部密度和距离的乘积,存在明显跳跃这一特征确定阈值,从而能自动确定聚类中心[3]。
- 根据决策图和簇中心权值排序图提出自动选取聚类中心的策略[4]。
- 利用加权的局部密度和相对距离乘积的斜率变化趋势实现聚类中心的自动选择[5]。
- 基于KL散度的参数指标,用于描述数据集点与其他点γ值的差异度之和,差异度越大,值越趋近于0[6]。
2.4 制定新的分配规则
- 定义新的数据点间邻近程度的度量准则。采用k近邻思想寻找密度峰值,将密度峰值的k个近邻点分配给其对应类簇,对所有已分配数据点寻找相互邻近度最高的未分配数据点,将未分配数据点分配给已分配数据点所在类簇[1]。
- 提出两种基于K近邻的样本分配策略,依次分配样本到相应类簇中心[7]。
2.5 改进距离矩阵
由于所使用的数据集的量纲存在不统一的问题和数值的数量级对数据分布和类别划分有一定影响,采用马氏距离替代原算法中的欧式距离来消除这种影响[2]。
三、聚类效果及其MATLAB代码
通过计算样本的局部密度和相对距离绘制决策图如图1所示。图中分布在右上角的样本具有非常高的 δ δ δ 值和 ρ ρ ρ 值,可以考虑选择这三个样本为密度峰值点,即聚类中心点。
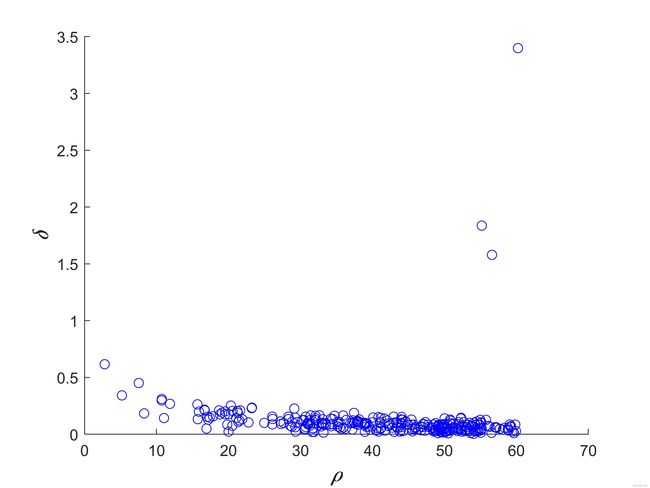
为了更准确的选择密度峰值点作为聚类中心点,可以对决策值 γ γ γ 进行降序排列如图2所示,进而选择前 k k k 个 γ γ γ 值最大的数据点作为聚类中心点。
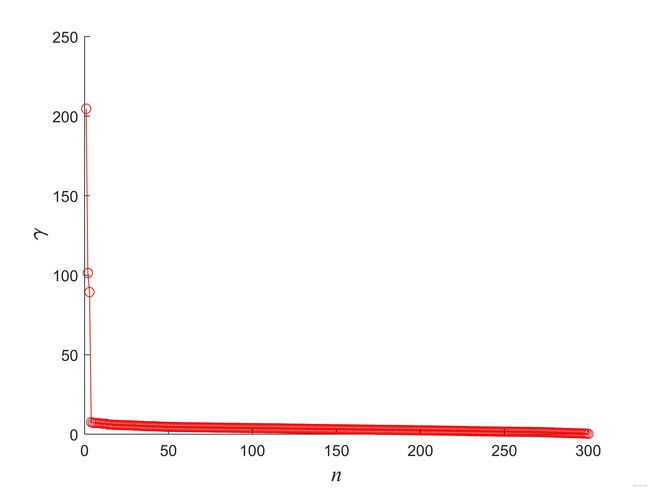
从图中可以看出,聚类中心点的数目为3,可以通过程序确定 γ γ γ 进行降序排列前的样本点所在下标,继而找到这三个聚类中心点。
数据集最终的聚类效果如下:
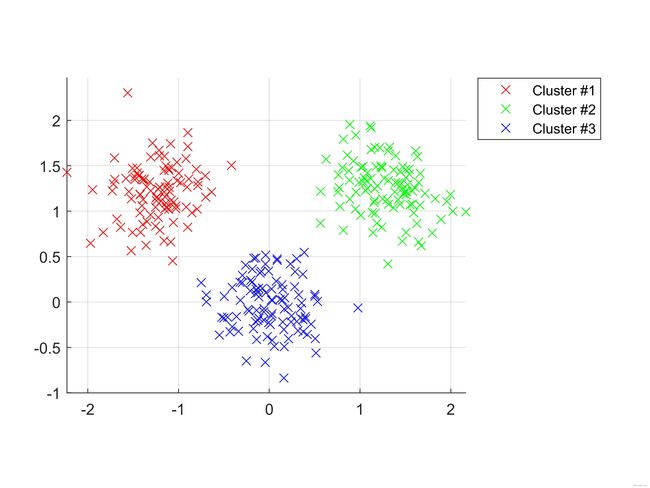
clc;
clear;
close all;
load x;
load Feature;
x = Feature';
dc = 0.5; % 邻域截断距离
s = 2; % 选择局部密度的计算方式
[rho,delta,gamma,cluster] = DPC(x,dc,s);
figure;
plot(rho,delta,'bo');
xlabel('\rho','FontAngle','italic','FontName','Times New Roman','FontWeight','bold','FontSize',14);
ylabel('\delta','FontAngle','italic','FontName','Times New Roman','FontWeight','bold','FontSize',14);
box off;
figure;
plot(gamma,'r-o');
xlabel('n','FontAngle','italic','FontName','Times New Roman','FontWeight','normal','FontSize',14);
ylabel('\gamma','FontAngle','italic','FontName','Times New Roman','FontWeight','bold','FontSize',14);
box off;
ShowClusterResult(x, cluster);
数据集以及完整代码见链接:密度峰值聚类算法(DPC)MATLAB代码
参考文献
[1] 赵嘉, 姚占峰, 吕莉, 等. 基于相互邻近度的密度峰值聚类算法[J]. 控制与决策, 2021, 36(3): 543-552.
[2] 辜振谱, 刘晓波, 韩子东, 等. 基于改进密度峰值聚类的航空发动机故障诊断[J]. 计算机集成制造系统, 2020, 26(5): 1211-1217.
[3] 王军华, 李建军, 李俊山, 等. 自适应快速搜索密度峰值聚类算法[J]. 计算机工程与应用, 2019, 55(24): 122-127.
[4] 吴斌, 卢红丽, 江惠君. 自适应密度峰值聚类算法[J]. 计算机应用, 2020, 40(6): 1654-1661.
[5] 王芙银, 张德生, 张 晓. 结合鲸鱼优化算法的自适应密度峰值聚类算法[J]. 计算机工程与应用, 2021, 57(3): 94-102.
[6] 丁志成, 葛洪伟, 周 竞. 基于KL散度的密度峰值聚类算法[J]. 重庆邮电大学学报(自然科学版), 2019, 31(3): 367-374.
[7] 谢娟英, 高红超, 谢维信. K近邻优化的密度峰值快速搜索聚类算法[J]. 中国科学:信息科学, 2016, 46(2): 258-280.
[8] LIU R, WANG H, YU X. Shared-nearest-neighbor-based clustering by fast search and find of density peaks[J]. Information Sciences, 2018, 450: 200-226.