Java数据结构与算法（更新中）

✨数据结构与算法

Github：https://github.com/sanshisi/DS

一、概念介绍

1.数据结构概述

数据之间的关系

1.1逻辑结构

• 线性结构：线性结构中的数据元素之间是一对一的关系
• 树形结构：树形结构中的数据元素之间存在一种一对一的层次关系
• 图形结构：图形结构的数据元素是多对多的关系

1.2物理结构

• 顺序存储结构：开辟一组连续的空间存储数据
• 链式存储结构：开辟一组随机的空间存储数据

2.算法概述

2.1什么是算法

是解决特定问题求解步骤的描述,分析问题，一步一步求解，并得到结果,这一系列的步骤就称之为算法

**例如：**1~100求和

=====方法一
int sum=0;
int N=100;
for(int i=1;i<=N;i++){
	sum+=i;
}
=====方法二
int N=100;
int sum=(N+1)*N/2;    

方案1随着N的增大，循环的次数也会增大，也就意味着执行的次数和运行的时间也会增大

方案2随着N的增大，其执行次数只有一次，不会随着N的增大而增大

同一个问题，可以有多种不同的解决方案，也就是说可以用不同的算法去解决同一个问题

2.2评价算法的好坏

• 事后统计法
• 事前分析法

2.3时间复杂度

算法时间复杂度主要探究的是问题输入规模N的数量级

不是算法的具体执行次数

---

常数阶O(1)

就是那些无循环、无递归、与问题输入规模N无关的、逐行执行的代码

int a = 3;
int b = 4;
int c = a + b;

---

线性阶O(n)

与问题输入规模有关的，主要是一层循环的代码，多个一层循环可以并列但不能包含

int N = 10;
for (int i = 1; i <= N; i++) {
    System.out.println(i);
}

int N = 10;
for (int i = 1; i <= N; i++) {
    System.out.println(i);
}
for (int i = 1; i <= N; i++) {
    System.out.println(i);
}

---

线性阶O(n+m)

和线性阶O(n)一样，只不过我们有两种数据的输入规模

int N = 10;
for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= N; j++) {
        System.out.println(i + j);
    }
}

---

平方阶O(n^2)

与问题输入规模有关的，主要是二层嵌套循环的代码

int N = 10;
for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= N; j++) {
        System.out.println(i + j);
    }
}

---

平方阶O(nm)

和平方阶O(n^2)一样，只不过我们有两种数据输入规模

int N = 10;
int M = 20;
for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= M; j++) {
        System.out.println(i + j);
    }
}

---

对数阶O(logn)

与问题输入规模有关的，主要是一层循环迭代或递归的代码

int count = 1;
int N = 100000;
while (count < N) 
    count = count * 2;

---

✨时间复杂度简单计算：忽略常数、只保留幂高项、且忽略幂高项的系数。

✨常见阶的比较：

二、动态数组

动态数组就是顺序存储结构具体实现的核心思想

1.数组概述

首先我们看一下Java内置数组

特点：

• 数组的长度一旦确定则不可更改
• 数组只能存储同一类型的数据
• 数组每个存储空间地址是连续且相等的
• 数组提供角标的方式访问元素

缺点：

• 长度不可变
• 地址连续且提供角标访问很快
• 数组只有length这个属性

因此我们想实现更多的功能通过动态数组

例如：

• 在任意位置添加删除元素
• 获取任意位置元素
• 更改某一位置元素数据
• 清空数组
• ……

2.线性表的实现

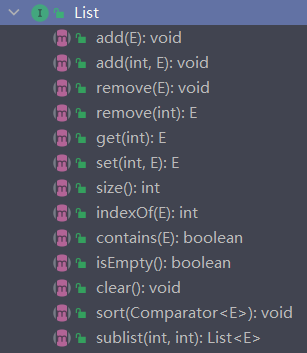
2.1List接口的定义

定义一系列例如添加、删除、大小、查找元素第一次出现的位置、元素是否在数组、数组是否为空、分割数组、数组排序、迭代……

代码位置：List.java

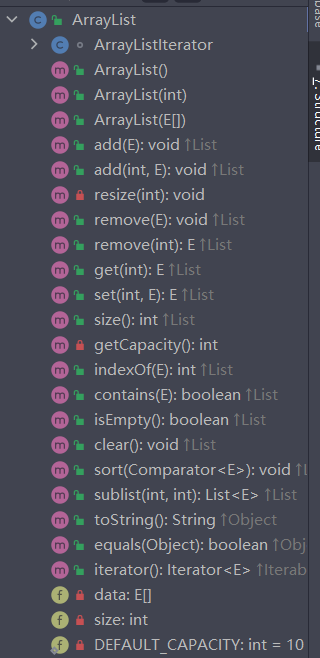
2.2实现ArrayList

✨具体实现

添加或删除会遇到的情况

扩容或缩容

...add() 
    // 当容量满了，扩两倍
    // 判读线性表是否满状态
    if (size == data.length) {
        resize(2 * data.length);
    }
...
    
...remove()
    // 什么时候缩容
    // 1.有效元素是容量的1/4
    // 2.当前容量不得小于的等于默认容量
    if (size == data.length / 4 && data.length > DEFAULT_CAPACITY) {
        resize(data.length / 2);
    }
...


// 扩容/缩容 操作 不向外界开放提供  是私有private
private void resize(int newLen) {
    E[] newData = (E[]) new Object[newLen];
    for (int i = 0; i < size; i++) {
        newData[i] = data[i];
    }
    data = newData;
}

---

排序

@Override
public void sort(Comparator<E> c) {
    if (c == null) {
        throw new IllegalArgumentException("comparator can not be null");
    }
    for (int i = 1; i < size; i++) {
        E e = data[i];
        int j = 0;
        for (j = i; j > 0 && c.compare(data[j - 1], e) > 0; j--) { // compare > 0 代表第一个值比第二个值大
            data[j] = data[j - 1];
        }
        data[j] = e;
    }
}

---

重写equals

@Override
public boolean equals(Object o) { // 比较的是两个 ArrayList 是否相等
    // 1.判空
    if (o == null) {
        return false;
    }
    // 2.判自己
    if (this == o) {
        return true;
    }
    // 3.判类型
    if (o instanceof ArrayList) {
        // 4.按照自己的逻辑比较
        ArrayList<E> other = (ArrayList<E>) o;
        // 5.先比较元素的个数
        if (this.size != other.size) {
            return false;
        }
        // 6.有效元素个数相等的情况下 逐个比较元素
        for (int i = 0; i < size; i++) {
            if (!data[i].equals(other.data[i])) {
                return false;
            }
        }
        return true;
    }
    return false;
}

---

重写迭代器

//获取当前这个数据结构/容器 的 迭代器
//通过迭代器对象 更方便挨个取出每一个元素
//同时 实现了Iterable 可以让当前的数据结构/容器 被foreach循环遍历
@Override
public Iterator<E> iterator() {
    return new ArrayListIterator();
}

//创建一个属于ArrayList的迭代器
class ArrayListIterator implements Iterator<E> {
    private int cur = 0;

    @Override
    public boolean hasNext() {//判断是否有下一个元素
        return cur < size;
    }

    @Override
    public E next() {//如果有下一个元素 则把当前元素返回 并移至到下一个元素
        return data[cur++]; // 先用后加
    }
}

……

代码位置：ArrayList.java

3.栈的实现

先进后出

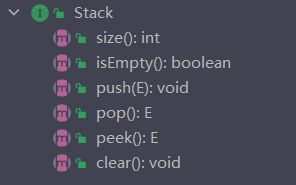
3.1Stack接口的定义

栈的方法

• 出栈
• 入栈
• 查看栈顶数据
• ……

因为是动态数组实现栈，所以我们实现出入栈都是对数组进行操作

入栈本质上就是在动态数组尾部添加一个数据

出栈本质上就是动态数组尾部删除一个数据

代码位置：Stack.java

3.2实现ArrayStack

代码位置：ArrayStack.java

3.3中缀表达式

传入一个表达式 (10+20/2*3)/2+8 对其进行计算

给定表达式：(10+20/2*3)/2+8

首先我们需要将表达式中的字符和数字分离，用到自定义方法insertBlanks()和字符串的split(),之后这些存入数组tokens中

=====insertBlanks()=====
//对原表达式进行格式化处理 给所有的非数字字符两边添加空格
private static String insertBlanks(String expression) {
    StringBuilder sb = new StringBuilder();
    for (int i = 0; i < expression.length(); i++) {
        char c = expression.charAt(i);
        if (c == '(' || c == ')' || c == '+' || c == '-' || c == '*' || c == '/') {
            sb.append(' ');
            sb.append(c);
            sb.append(' ');
        } else {
            sb.append(c);
        }
    }
    return sb.toString();
}

接下来思路就很简单了，依次遍历数组tokens，取出元素放入numberStack、operatorStack两个栈中，然后在根据符号进行弹栈操

举个例子：

1*2+3

需要遍历5次

第1次遍历：

1直接放入数字栈

numberStack : [1]

operatorStack : []

第2次遍历：

+，符号栈为空，直接放入符号栈

numberStack : [1]

operatorStack : [*]

第3次遍历：

2直接放入数字栈

numberStack : [1,2]

operatorStack : [*]

第4次遍历：

+,此时符号栈已经有乘号了，并且乘号优先级比加号高，所以应当进行弹栈计算，将得到的结果放入数字栈

numberStack : [2]

operatorStack : [+]

第5次遍历：

3直接放入数字栈

numberStack : [2,3]

operatorStack : [+]

最后

将数字栈和符号栈中的元素依次弹出计算

代码位置：InfixCalculator.java

3.4中缀转后缀 -> 后缀表达式 做计算器(逆波兰表达式)

中缀转后缀

将中缀表达式转换为后缀表达式，更为容易计算

中缀形式：(10+20/2*3)/2+8
后缀形式：10 20 2 / 3 * + 2 / 8 + 

需要使用一个符号栈和一个数组进行存储数据

大概原理：遍历中缀表达式，如果是数字，直接存入数组中，遇到符号，首先判断优先级，如果栈顶优先级更高或相等，则将栈顶符号放入数组中，如果是左括号，则将左括号入符号栈，如果是右括号，则将符号栈中左括号上的符号依次弹出放入数组中（注：括号不需要放入数组），遍历到最后，如果符号栈不为空，依次将符号栈中元素弹出放入数组中就好了

代码位置：InfixToSuffix.java

逆波兰表达式：使用后缀表达式做计算器

代码位置：SuffixCalculator.java

3.5进制转换

✨掌握好如何使用ASCAll码

十进制转十六进制-

代码位置：DecToHex.java

十六进制转十进制

代码位置：HexToDec.java

3.6回文判断

法1：

每次入栈前要判断该值和栈顶值是否相等，如果相等就进行弹栈操作，最后通过判断栈是否为空来决定是否为回文

但是有一个bug，就是遇上aabbccdd这种也会判断成回文

法2：

通过双指针方法进行遍历字符串，解决了法一的bug

代码位置：JudgingPalindrome.java

3.7括号匹配

法1：

jshell> '(' - ')'
$2 ==> -1
    
jshell> '[' - ']'
$3 ==> -2
    
jshell> '{' - '}'
$4 ==> -2

通过Ascall码可以知道，（）[] {} 左括号和右括号的差值为-1或-2，可以利用这个方法进行括号匹配

法2：

通过HashMap来做

HashMap<Character,Character> map = new HashMap<>();
map.put('[',']');
map.put('<','>');
map.put('(',')');
map.put('{','}');

只需要进行判断 栈顶元素是否是map中的键 && 该键对应的值是否等于遍历字符串的值

代码位置：MatchBracket.java

3.8双端栈的实现

只是将栈的方法拓宽了，代码实现其实不是很难

代码位置：ArrayDoubleEndStack.java

4.队列的实现

栈是先进先出

4.1Queue接口的定义

offer()		入队列
poll()		出队列
element()	查看队首元素

代码位置：Queue.java

4.2实现ArrayQueue

代码位置:ArrayQueue.java

4.3文件遍历

同过对队列实现文件遍历，只要队列不为空，则出队一个目录对象，将该目录对象展开，开始遍历，遇到文件则打印名称，遇到其他目录 则进队

代码位置:DiretoryTraversal.java

4.4栈实现队列

这里需要两个栈：A栈和B栈

其中真正用来存放数据的是A栈，B栈仅做中转用

假设A栈中有三个元素：1,2,3

现在进行出队列：出的是1，所以需要先依次将A栈中的3,2出栈，存入B栈中，再将1出栈返回，之后再将B栈中的元素依次出栈放入A栈中即可

如果是进行入队列：直接人A栈即可

代码位置:StackToQueue.java

4.5队列实现栈

这里需要两个队列：A队列和B队列

两个队列可以轮流存储数据

假设在A中入了三个元素：1,2,3

现在进行出栈：出的是3，需要依次将A中的1,2出了，存入B中，然后再将3出队列返回即可，此时数据就全在B中

现在进行查看栈顶元素：栈顶元素为2，B中元素1,2，需要将B中1出队列，存入A队列中，然后在将1出队列，在返回前，将1入A队列，

此时元素就全存在了A栈中

代码位置:QueueToStack.java

4.6循环队列

将普通的队列变成一个循环队列，节省空间，因此需要定义一个头指针和尾指针

需要预留一个位置空给尾指针

假设不留空，那么就会导致判断空或者满的时候判断条件是一样的

因此我们需要留一个位置给尾指针，用来改变判断条件

代码位置:ArrayLoopQueue.java

4.7双端队列

其实就是循环队列的升级版

只是在其中加了一些对栈方法的实现

代码位置:ArrayDeque.java

三、动态链表

1.单项链表

每个节点只存储数值和指向下一个节点

✨节点定义

// 定义节点对象
private class Node {
    E data;
    Node next;

    public Node() {
        this(null, null);
    }

    public Node(E data) {
        this(data, null);
    }

    public Node(E data, Node next) {
        this.data = data;
        this.next = next;
    }

    @Override
    public String toString() {
        return data.toString();
    }
}

代码位置:LinkedSinglyList.java

2.单项循环链表

在单项链表的基础上将首尾链接在了一起

✨节点定义

//定义结点对象
private class Node {
    E data;     //数据域
    Node next;  //指针域

    public Node() {
        this(null, null);
    }

    public Node(E data) {
        this(data, null);
    }

    public Node(E data, Node next) {
        this.data = data;
        this.next = next;
    }

    @Override
    public String toString() {
        return data.toString();
    }
}

代码位置:LinkedSinglyCircularList.java

约瑟夫环

据说著名犹太历史学家Josephus有过一下的故事:

在罗马人占领乔塔帕特后，39个犹太人与Josephus及他的朋友躲在一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3个人该人必须自杀，然后再由下一个重新报数,直到所有人都自杀身亡为止。

然而Josephus和他的朋友并不想遵从, Josephus要他的朋友先假装遵从，他将朋友与自己安排在了第16个与第31个位置，于是逃过了这场死亡游戏。

//约瑟夫环问题
public void josephusLoop() {
    if (size <= 2) {
        return;
    }
    Node p = head;
    while (size != 2) {
        p = p.next;
        Node del = p.next;
        if (del == head) {
            head = del.next;
        } else if (del == tail) {
            tail = p;
        }
        p.next = del.next;
        del.next = null;
        p = p.next;
        size--;
    }
}

逢七过游戏

//逢七过游戏
/*
输入玩家的个数
输入从哪个玩家开始
输入该玩家从哪个数字开始
输入一共玩几个数字
打印出每个玩家将要报出的所有数字
*/

代码位置:SevenGame.java

3.双向循环链表

每个节点存储了 元素和指向上一个节点的指针和指向下一个节点的指针

首尾相连接

✨节点定义

private class Node {
    E data;
    Node pre;   //直接前驱
    Node next;  //直接后继

    public Node() {
        this(null, null, null);
    }

    public Node(E data) {
        this(data, null, null);
    }

    public Node(E data, Node pre, Node next) {
        this.data = data;
        this.pre = pre;
        this.next = next;
    }

    @Override
    public String toString() {
        return data.toString();
    }
}

代码位置:LinkedList.java

四、分治回溯

1.棋盘覆盖

博客位置：https://blog.csdn.net/weixin_46049759/article/details/122574014

2.汉诺塔

代码位置:LinkedList.java

3.全排列

代码位置:LinkedList.java

4.迷宫问题

代码位置:LinkedList.java

5.N皇后问题

代码位置:LinkedList.java

6.数独

博客位置：https://blog.csdn.net/weixin_46049759/article/details/122628294

五、排序算法

1.冒泡排序

遍历数组，两两比较，如果前一个数大于后一个数就交换两个数，每次循环都会找出最大的那个数

for (int i = 0; i < arr.length - 1; i++) {
    for (int j = 0; j < arr.length - i - 1; j++) {
        if (arr[j] > arr[j + 1]) {
            swap(j, j + 1);
        }
    }
}

代码位置:BubbleSort.java

2.插入排序

这个可以类似于小朋友排队，我们先默认第一个是有序的，然后开始将第二个小朋友依次和前面的小朋友进行比较，如果小于前面的就交换，大于就不动

for (int i = 1; i < arr.length; i++) {
    int e = arr[i]; // 选中要和前面比较的小盆友
    int j = 0;
    for (j = i; j > 0 && arr[j - 1] > e; j--) { // 从有序的队伍后面向前比较
        arr[j] = arr[j - 1]; // 如果前面的比他大,就把前面的向后移动一位
    }
    arr[j] = e;
}

代码位置:InsertionSort.java

3.选择排序

对数组进行遍历，需要每次找到剩余元素最小的和当前元素交换

for (int i = 0; i < arr.length - 1; i++) {
    for (int j = i + 1; j < arr.length; j++) {
        if (arr[i] > arr[j]) { // 如果后面元素比当前元素更小，就进行交换
            swap(i, j);
        }
    }
}

代码位置:SelectionSort.java

4.希尔排序

插入排序的升级版，又叫缩小增量排序

9 8 7 6 5 4 3 2 4 0

0 1 2 3 4 5 6 7 8 9

先去长度10一半，间隔为5，角标0,5进行比较大小(角标0,5中间间隔5个)，如果后面小于前面的则交换数据(插入排序)，然后依次是角标1,6；2,8……

然后再取间隔的一半，间隔为2，角标0,2进行比较，之后角标1,3进行比较，之后角标2,4进行比较，角标2,4比较完后，还可以继续向前比较角标0,2……

……

间隔为1，两两比较

int len = arr.length;
// O(n^1.3)
for (int gap = len / 2; gap > 0; gap = gap / 2) { // 每次取间隔为一半
    for (int i = gap; i < len; i++) {
        int e = arr[i];
        int j = i;
        while (j - gap >= 0 && arr[j - gap] > e) { // 插入排序的体现
            arr[j] = arr[j - gap];
            j = j - gap;
        }
        arr[j] = e;
    }
}

代码位置:ShellSort.java

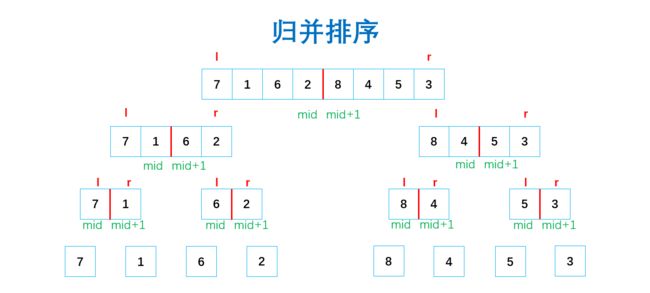
5.归并排序

依次对半分，一直分到最小一个，然后开始合并，合并的时候其实可以理解为【合并两个有序数组】

代码位置:MergeSort.java

6.快排

单路快排

首先选中一个数（可以是默认第一个数，也可以是随机一个数组中的数）作为中间的数，然后将小于他的数全部放它的左边，将大于它的数全部放在右边，然后第二步，从角标0到刚刚那个中间的数再做这样的操作，从中间的数到最后一个数也做这样的操作，第三步……

代码位置:QuickSort01.java

---

双路快排

代码位置:QuickSort02.java

---

三路快排

代码位置:QuickSort03.java

7.基数排序

代码位置:RadixSort.java

8.桶排序

代码位置:BucketSort.java

9.计数排序

代码位置:CountingSort.java

10.插值查找

代码位置:InterpolationSearch.java

11.堆排序

六、树与哈希表

1.二分搜索树

二分搜索树本身就是二叉树，只不过在二叉树上面加了一些规则

博客位置：树与哈希表—二分搜索树(BST)

代码位置:BinarySearchTree.java

2.集合二分搜索树实现

集合的底层由二分搜索数实现

代码位置:TreeSet.java

3.集合链表实现

集合的底层由链表实心

读取文件中的单词

代码位置:LinkedSet.java

4.Map二分搜索树实现

本质上和二分搜索数还是一样的，只不过是Map

代码位置:TreeMap.java

5.AVL平衡树

✨对于任意一个节点,左子树和右子树的高度差不能超过1

名字缘由：G.M.Adelson-Velsky和E.M.Landis

是一种最早的自平衡二分搜索树结构

满二叉树一定是平衡二叉树，高度最低

完全二叉树也是平衡二叉树，叶子节点深度相差不为1

AVL平衡树是对BST二分搜索树进行了改善

博客位置：树与哈希表—二分平衡树(AVL)

代码位置:AVLTreeMap.java

6.最大堆

博客位置：树与哈希表—最大堆

代码位置:MaxHeap.java

7.优先队列最大堆实现

代码位置:PriorityQueue.java

8.Tire树

代码位置:Trie.java

9.哈希表

代码位置:HashTable.java