23种激活函数
文章目录
-
- 一、简介
- 二、激活函数种类
-
- 1、恒等函数
- 2、单位阶跃函数
- 3、逻辑函数
- 4、双曲正切函数
- 5、反正切函数
- 6、Softsign函数
- 7、反平方根函数(ISRU)
- 8、线性整流函数(ReLU)
- 9、带泄露线性整流函数(Leaky ReLU)
- 10、参数化线性整流函数(PReLU)
- 11、带泄露随机线性整流函数(RReLU)
- 12、指数线性函数(ELU)
- 13、扩展指数线性函数(SELU)
- 14、S型线性整流激活函数(SReLU)
- 15、反平方根线性函数(ISRLU)
- 16、自适应分段线性函数(APL)
- 17、SoftPlus函数
- 18、弯曲恒等函数
- 19、Sigmoid Weighted Liner Unit(SiLU)
- 20、SoftExponential
- 21、正弦函数
- 22、Sinc函数
- 23、高斯函数
一、简介
一个节点的激活函数(Activation Function)定义了该节点在给定的输入或输入的集合下的输出。神经网络中的激活函数用来提升网络的非线性(只有非线性的激活函数才允许网络计算非平凡问题),以增强网络的表征能力。对激活函数的一般要求是:必须非常数、有界、单调递增并且连续,并且可导。
在实际选择激活函数时并不会严格要求可导,只需要激活函数几乎在所有点可导即可,即在个别点不可导是可以接受的。另外,其导数尽可能的大可以帮助加速训练神经网络,否则导数过小会导致网络无法继续训练下去。
二、激活函数种类
下面是不同的激活函数的函数公式,图像和导数公式,图像。
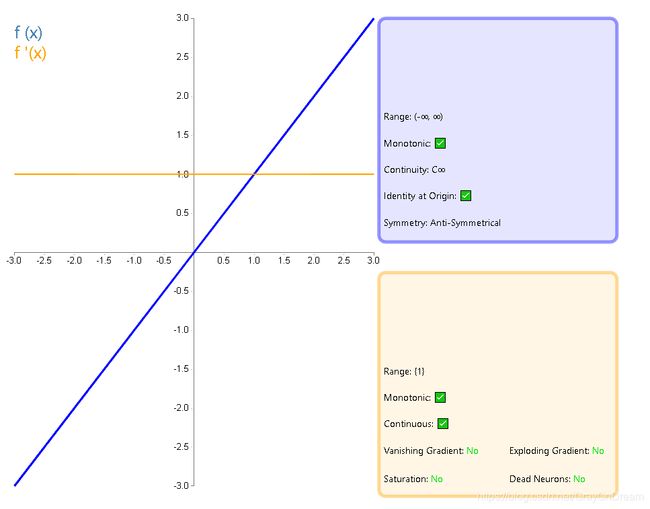
1、恒等函数
f ( x ) = x f ′ ( x ) = 1 f(x)=x \qquad\qquad\qquad f^{'}(x)=1 f(x)=xf′(x)=1
2、单位阶跃函数
f ( x ) = { 0 , x < 0 1 , x ≥ 0 f ′ ( x ) = { 0 , x ≠ 0 ? , x = 0 f(x)=\left\{\begin{array} {ll} 0,x < 0\\1,x\ge 0 \end{array}\right.\qquad\qquad f^{'}(x)=\left\{\begin{array} {ll} 0,x \ne 0\\?,x= 0 \end{array}\right. f(x)={0,x<01,x≥0f′(x)={0,x=0?,x=0

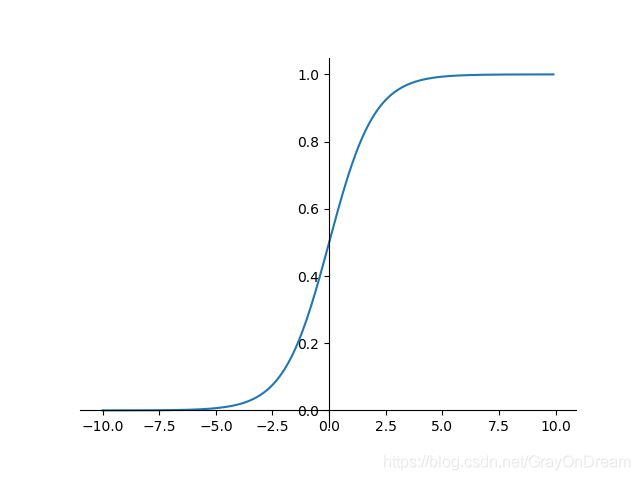
3、逻辑函数
f ( x ) = σ ( x ) = 1 1 + e − x f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f(x)=\sigma(x)=\frac{1}{1+e^{-x}}\qquad\qquad f^{'}(x)=f(x)(1-f(x)) f(x)=σ(x)=1+e−x1f′(x)=f(x)(1−f(x))
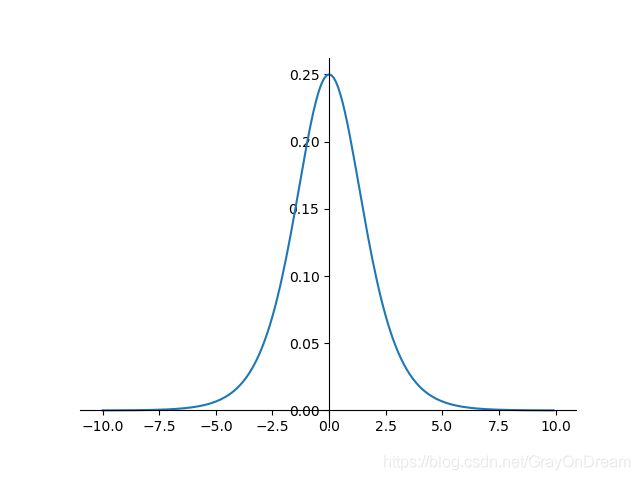
4、双曲正切函数
f ( x ) = t a n h ( x ) = ( e x − e − x ) e x + e − x f ′ ( x ) = 1 − f ( x ) 2 f(x)=tanh(x)=\frac{(e^x-e^{-x})}{e^x+e^{-x}}\qquad \qquad f^{'}(x)=1-f(x)^2 f(x)=tanh(x)=ex+e−x(ex−e−x)f′(x)=1−f(x)2

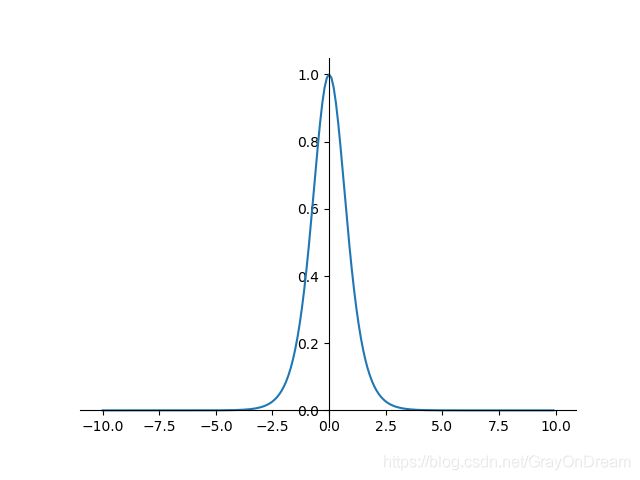
5、反正切函数
f ( x ) = t a n − 1 ( x ) f ′ ( x ) = 1 x 2 + 1 f(x)=tan^{-1}(x)\qquad\qquad f^{'}(x)=\frac{1}{x^2+1} f(x)=tan−1(x)f′(x)=x2+11
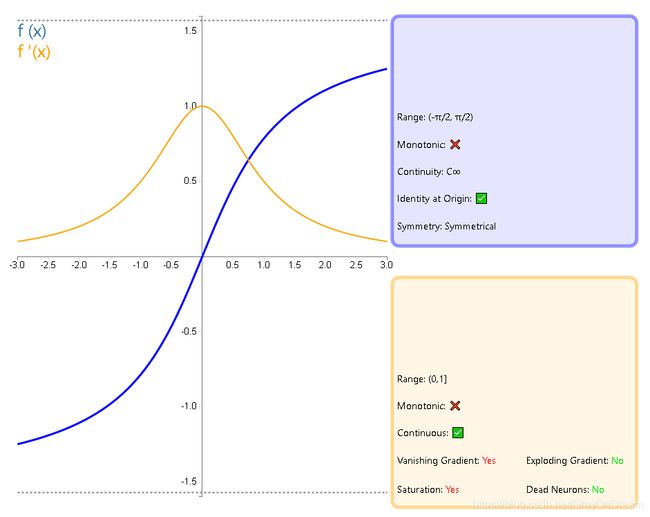
6、Softsign函数
f ( x ) = x 1 + ∣ x ∣ f ′ ( x ) = 1 ( 1 + ∣ x ∣ ) 2 f(x)=\frac{x}{1+|x|}\qquad\qquad f^{'}(x)=\frac{1}{(1+|x|)^2} f(x)=1+∣x∣xf′(x)=(1+∣x∣)21
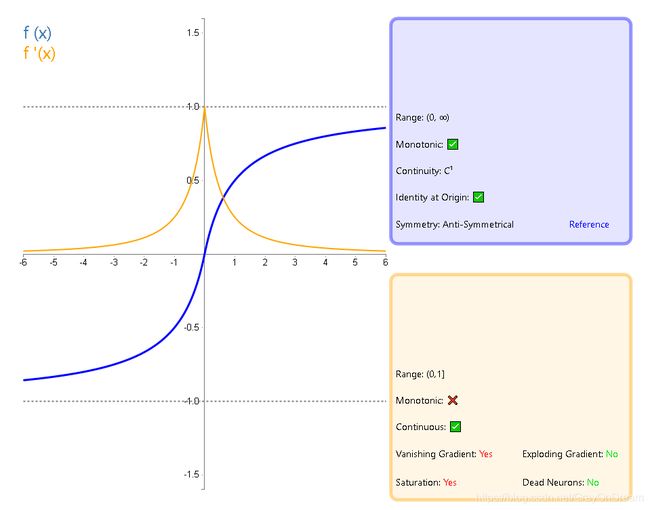
7、反平方根函数(ISRU)
f ( x ) = x 1 + α x 2 f ′ ( x ) = ( 1 1 + α x 2 ) 3 f(x)=\frac{x}{\sqrt{1+\alpha x^2}}\qquad \qquad f^{'}(x)=(\frac{1}{\sqrt{1+\alpha x^2}})^3 f(x)=1+αx2xf′(x)=(1+αx21)3
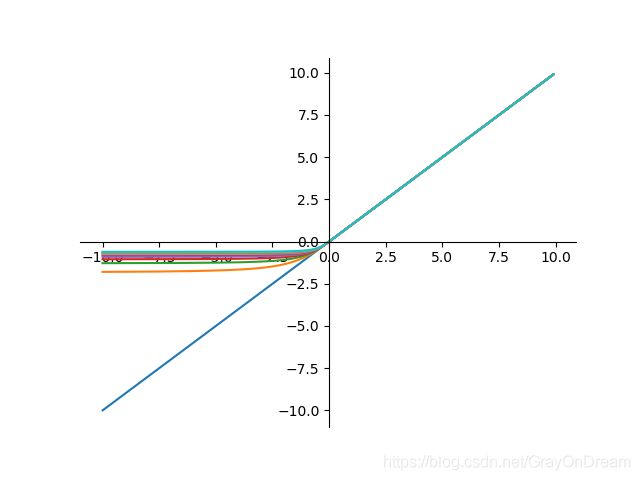
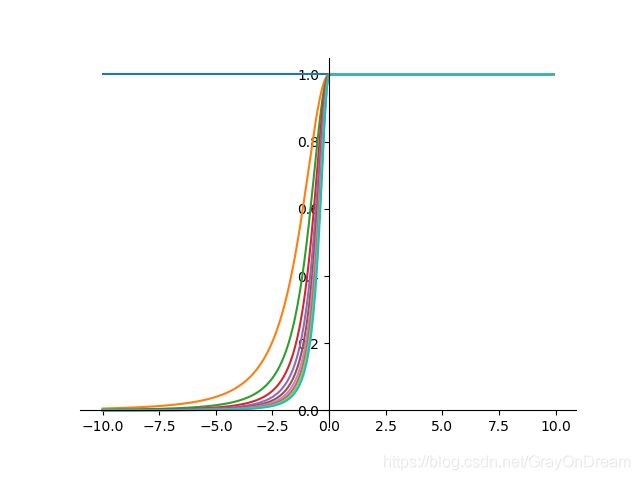
8、线性整流函数(ReLU)
f ( x ) = { 0 , x < 0 x , x ≥ 0 f ′ ( x ) = { 0 , x < 0 1 , x ≥ 0 f(x)= \left\{\begin{array}{ll}0,x<0\\x,x\ge 0 \end{array}\right.\qquad\qquad f^{'}(x)=\left\{\begin{array}{ll}0,x<0\\1,x\ge 0 \end{array}\right. f(x)={0,x<0x,x≥0f′(x)={0,x<01,x≥0
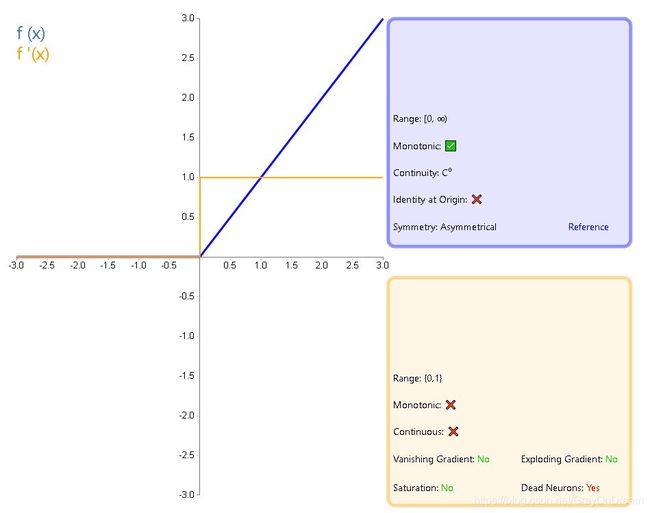
9、带泄露线性整流函数(Leaky ReLU)
f ( x ) = { 0.01 x , x < 0 x , x ≥ 0 f ′ ( x ) = { 0.01 , x < 0 1 , x ≥ 0 f(x)= \left\{\begin{array}{ll}0.01x,x<0\\x,x\ge 0 \end{array}\right.\qquad\qquad f^{'}(x)=\left\{\begin{array}{ll}0.01,x<0\\1,x\ge 0 \end{array}\right. f(x)={0.01x,x<0x,x≥0f′(x)={0.01,x<01,x≥0
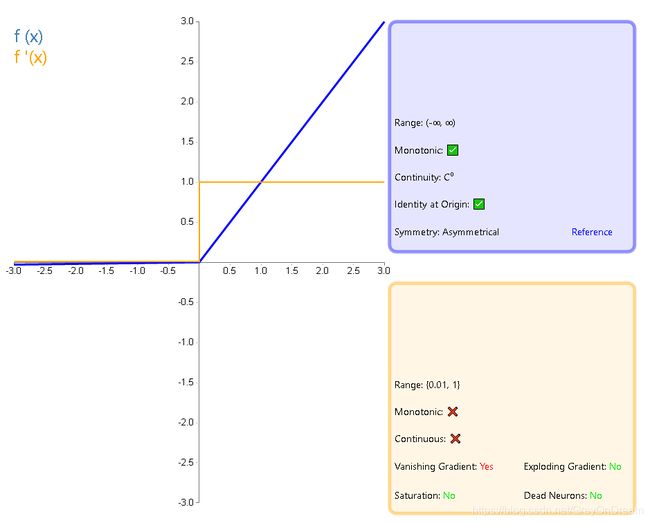
10、参数化线性整流函数(PReLU)
f ( x ) = { α x , x < 0 x , x ≥ 0 f ′ ( x ) = { α , x < 0 1 , x ≥ 0 f(x)= \left\{\begin{array}{ll}\alpha x,x<0\\x,x\ge 0 \end{array}\right.\qquad\qquad f^{'}(x)=\left\{\begin{array}{ll}\alpha,x<0\\1,x\ge 0 \end{array}\right. f(x)={αx,x<0x,x≥0f′(x)={α,x<01,x≥0
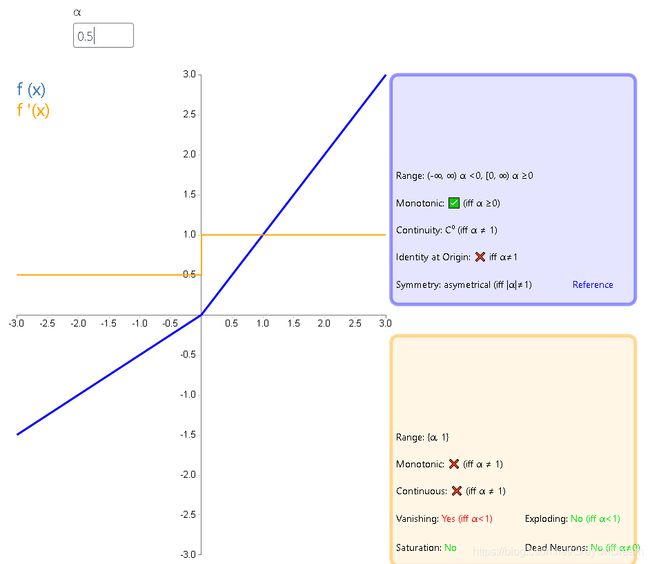
11、带泄露随机线性整流函数(RReLU)
f ( x ) = { α x , x < 0 x , x ≥ 0 f ′ ( x ) = { α , x < 0 1 , x ≥ 0 f(x)= \left\{\begin{array}{ll}\alpha x,x<0\\x,x\ge 0 \end{array}\right.\qquad\qquad f^{'}(x)=\left\{\begin{array}{ll}\alpha,x<0\\1,x\ge 0 \end{array}\right. f(x)={αx,x<0x,x≥0f′(x)={α,x<01,x≥0
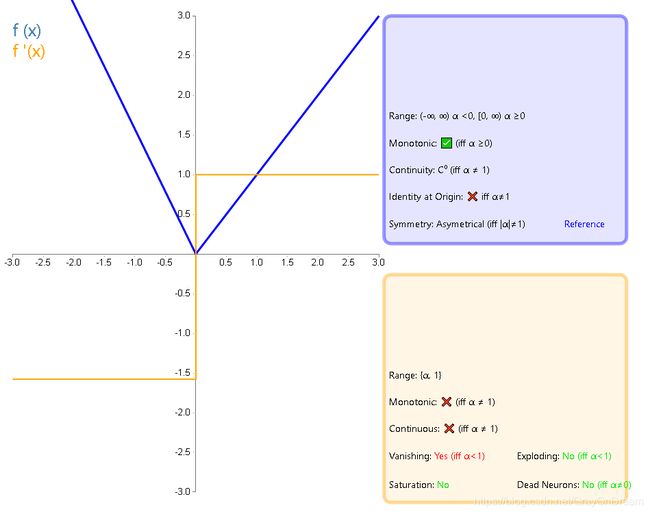
12、指数线性函数(ELU)
f ( x ) = { α ( e x − 1 ) , x < 0 x , x ≥ 0 f ′ ( x ) = { f ( α , x ) + α , x < 0 1 , x ≥ 0 f(x)= \left\{\begin{array}{ll}\alpha(e^x-1),x<0\\x,x\ge 0 \end{array}\right.\qquad\qquad f^{'}(x)=\left\{\begin{array}{ll}f(\alpha,x)+\alpha,x<0\\1,x\ge 0 \end{array}\right. f(x)={α(ex−1),x<0x,x≥0f′(x)={f(α,x)+α,x<01,x≥0
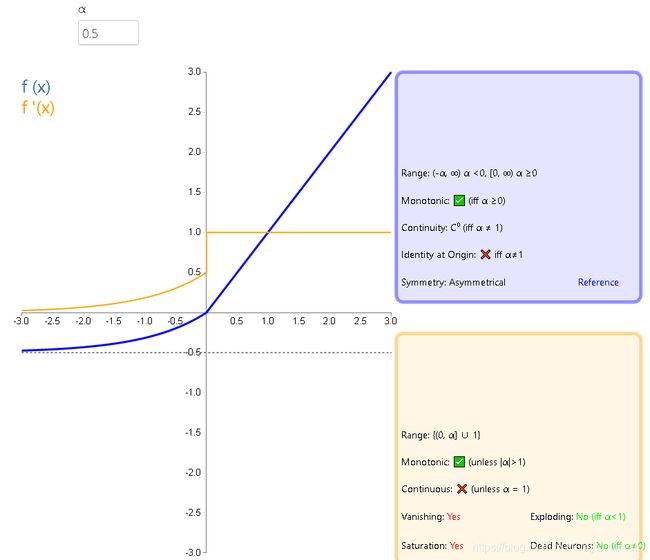
13、扩展指数线性函数(SELU)
f ( x ) = λ { α ( e x − 1 ) , x < 0 x , x ≥ 0 λ = 1.0507 , α = 1.67326 f ′ ( x ) = λ { α ( e x ) , x < 0 1 , x ≥ 0 \begin{aligned} f(x)=\lambda \left\{\begin{array}{ll}\alpha(e^x-1),x<0\\x,x\ge 0 \end{array}\right. \\ \lambda=1.0507,\alpha=1.67326 \end{aligned} \qquad\qquad f^{'}(x)=\lambda \left\{\begin{array}{ll}\alpha(e^x),x<0\\1,x\ge 0 \end{array}\right. f(x)=λ{α(ex−1),x<0x,x≥0λ=1.0507,α=1.67326f′(x)=λ{α(ex),x<01,x≥0
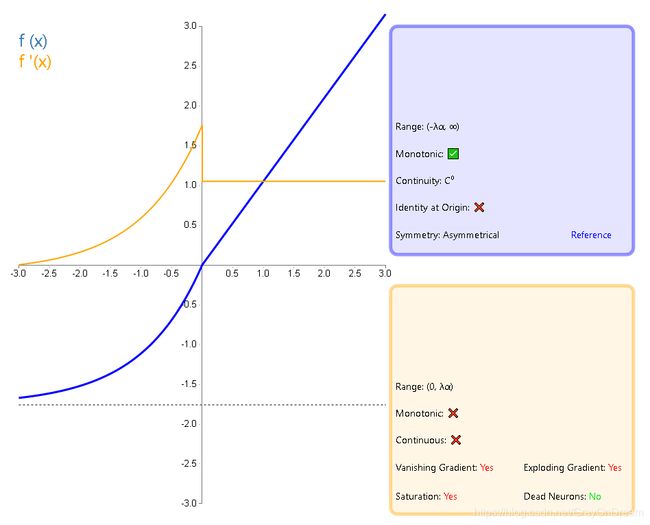
14、S型线性整流激活函数(SReLU)
f t l , a l , t r , a r ( x ) = { t l + a l ( x − t l ) , x ≤ t l x , t l < x < t r t r + a r ( x − t r ) , x ≥ t r t l , a l , t r , a r 为 参 数 f t l , a l , t r , a r ′ ( x ) = { a l , x ≤ t l 1 , t l < x < t r a r , x ≥ t r \begin{aligned} f_{t_l,a_l,t_r,a_r}(x)=\left\{\begin{array} {ll} t_l+a_l(x-t_l),x\le t_l\\ x,t_l
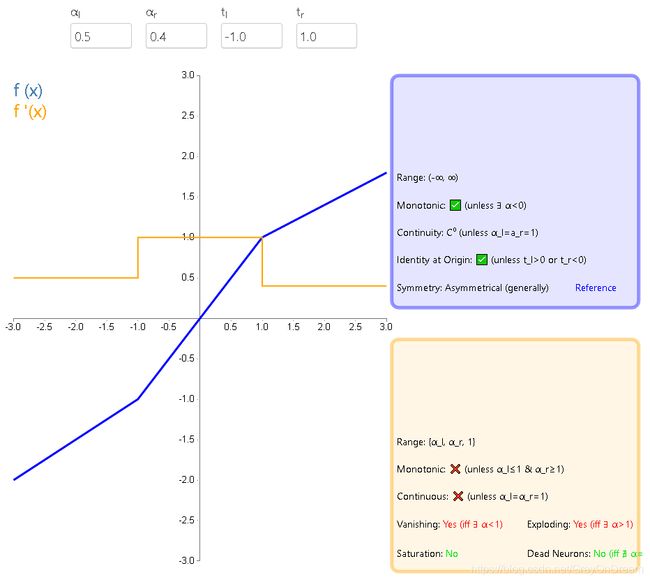
15、反平方根线性函数(ISRLU)
f ( x ) = { x 1 + α x 2 , x < 0 x , x ≥ 0 f ′ ( x ) = { ( 1 1 + α x 2 ) 3 , x < 0 1 , x ≥ 0 f(x)= \left\{\begin{array}{ll}\frac{x}{\sqrt{1+\alpha x^2}},x<0\\x,x\ge 0 \end{array}\right.\qquad\qquad f^{'}(x)=\left\{\begin{array}{ll}(\frac{1}{\sqrt{1+\alpha x^2}})^3,x<0\\1,x\ge 0 \end{array}\right. f(x)={1+αx2x,x<0x,x≥0f′(x)={(1+αx21)3,x<01,x≥0
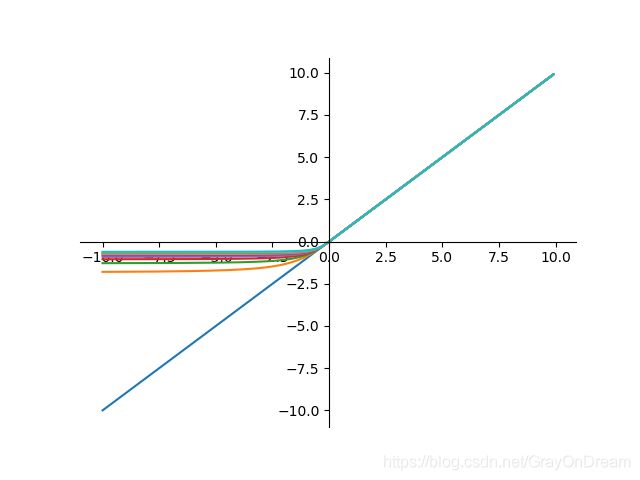

16、自适应分段线性函数(APL)
f ( x ) = m a x ( 0 , x ) + ∑ s = 1 S a i s m a x ( 0 , − x + b i s ) f ′ ( x ) = H ( x ) − ∑ s = 1 S a i s H ( − x + b i s ) f(x)=max(0,x)+\sum_{s=1}^{S}a^s_{i}max(0,-x+b^s_i)\qquad\qquad f^{'}(x)=H(x)-\sum^{S}_{s=1}a^s_iH(-x+b^s_i) f(x)=max(0,x)+s=1∑Saismax(0,−x+bis)f′(x)=H(x)−s=1∑SaisH(−x+bis)
17、SoftPlus函数
f ( x ) = ln ( 1 + e x ) f ′ ( x ) = e x 1 + e x f(x)=\ln(1+e^x) \qquad\qquad f^{'}(x)=\frac{e^x}{1+e^x} f(x)=ln(1+ex)f′(x)=1+exex
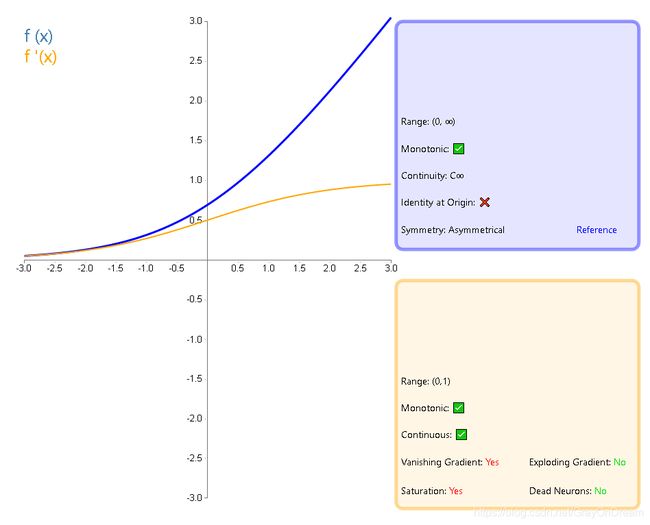
18、弯曲恒等函数
f ( x ) = x 2 + 1 − 1 2 + x f ′ ( x ) = x 2 x 2 + 1 + 1 f(x)=\frac{\sqrt{x^2+1}-1}{2}+x\qquad\qquad f^{'}(x)=\frac{x}{2\sqrt{x^2+1}}+1 f(x)=2x2+1−1+xf′(x)=2x2+1x+1
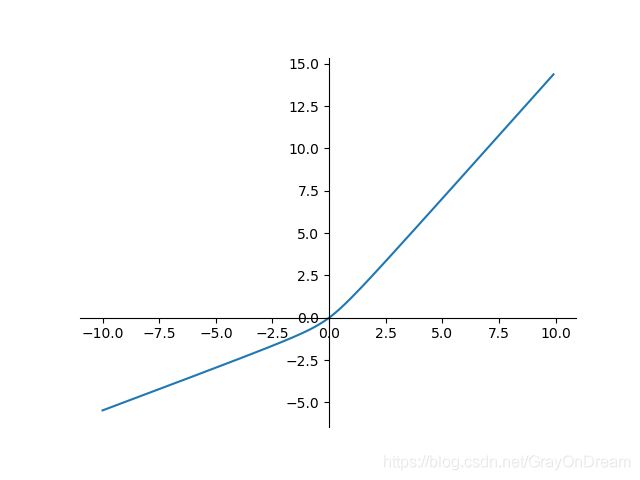
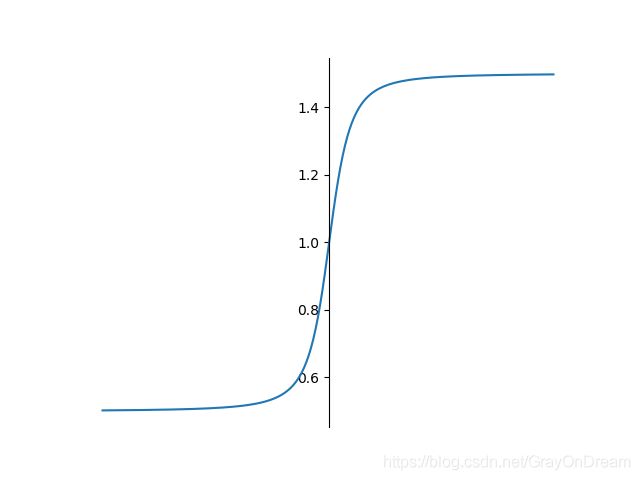
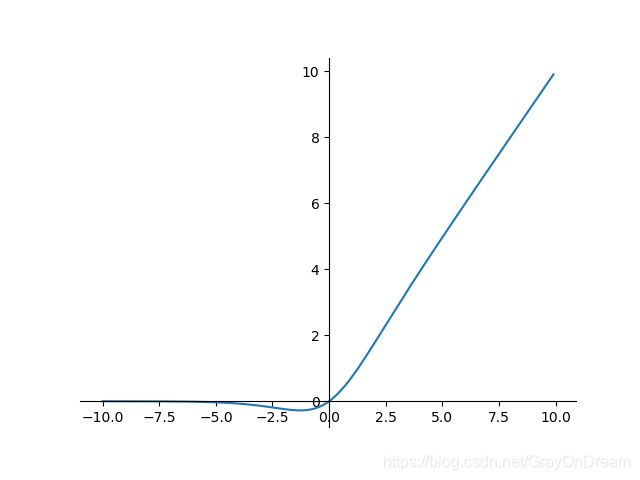
19、Sigmoid Weighted Liner Unit(SiLU)
f ( x ) = x ⋅ σ ( x ) f ′ ( x ) = f ( x ) + σ ( x ) ( 1 − f ( x ) ) f(x)=x\cdot \sigma(x) \qquad\qquad f^{'}(x)=f(x)+\sigma(x)(1-f(x)) f(x)=x⋅σ(x)f′(x)=f(x)+σ(x)(1−f(x))
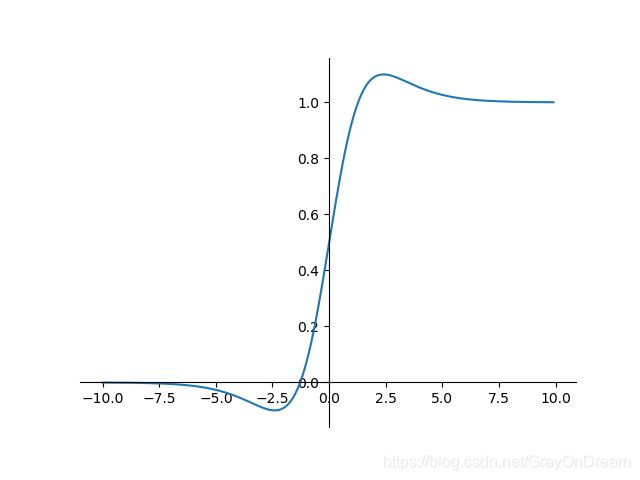
20、SoftExponential
f ( x ) = { − l n ( 1 − α ( x + α ) ) α , α < 0 x , α = 0 e α x − 1 α , α > 0 f ′ ( x ) = { 1 1 − α ( α + x ) , α < 0 e α x , α ≥ 0 f(x)= \left\{\begin{array} {ll} -\frac{ln(1-\alpha(x+\alpha))}{\alpha}, \alpha < 0\\ x,\alpha=0\\ \frac{e^{\alpha x}-1}{\alpha},\alpha >0 \end{array}\right. \qquad\qquad f^{'}(x)=\left\{\begin{array} {ll} \frac{1}{1-\alpha(\alpha+x)},\alpha < 0\\ e^{\alpha x},\alpha \ge 0 \end{array}\right. f(x)=⎩⎨⎧−αln(1−α(x+α)),α<0x,α=0αeαx−1,α>0f′(x)={1−α(α+x)1,α<0eαx,α≥0
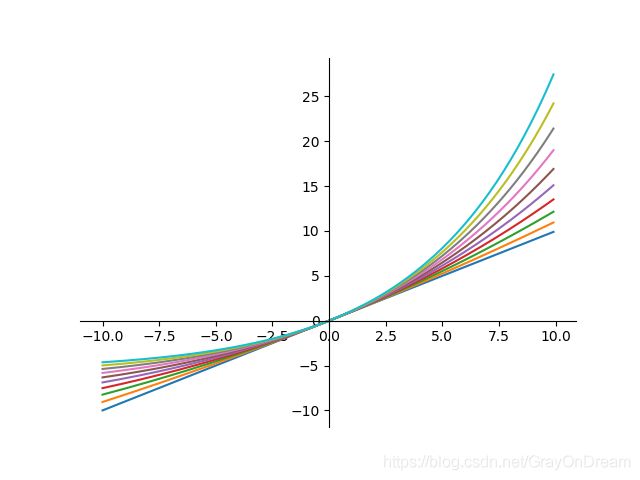
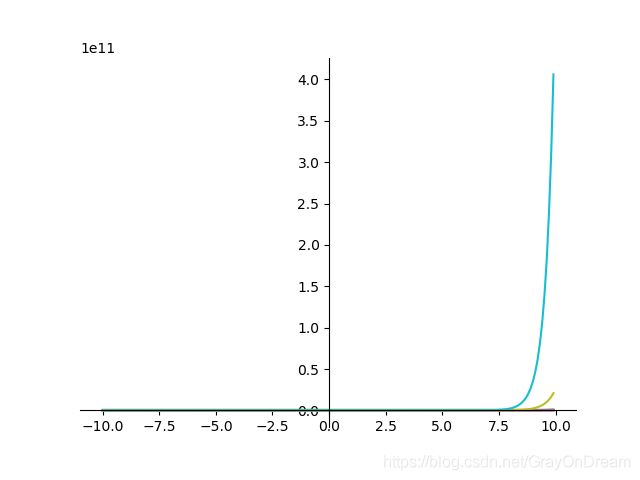
21、正弦函数
f ( x ) = s i n ( x ) f ′ ( x ) = c o s ( x ) f(x)= sin(x)\qquad\qquad f^{'}(x)=cos(x) f(x)=sin(x)f′(x)=cos(x)
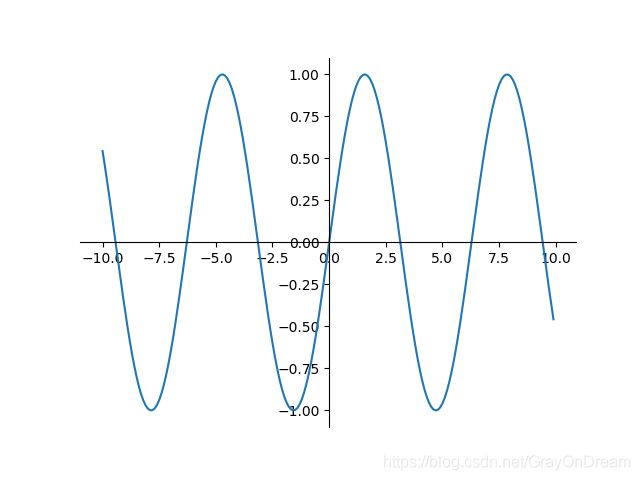
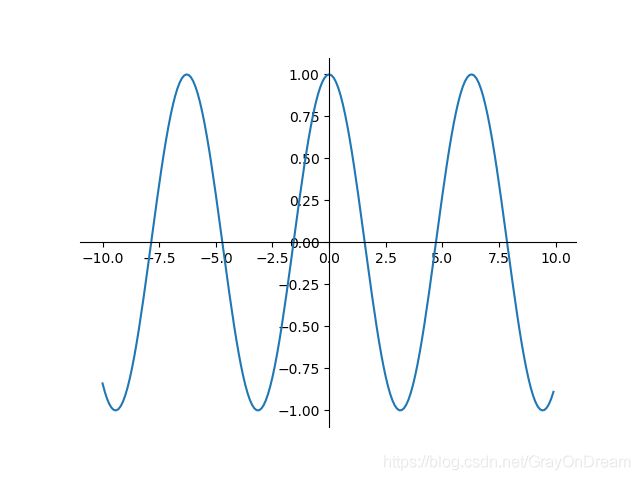
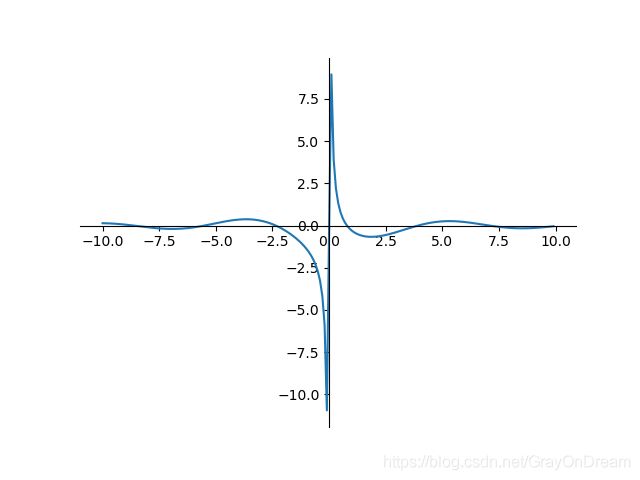
22、Sinc函数
f ( x ) = { 1 , x = 0 s i n ( x ) x , x ≠ 0 f ( x ) = { 0 , x = 0 c o s ( x ) x − s i n ( x ) x , x ≠ 0 f(x)=\left\{\begin{array} {ll} 1,x=0 \\ \frac{sin(x)}{x},x\ne 0 \end{array}\right.\qquad \qquad f(x)=\left\{\begin{array} {ll} 0,x=0 \\ \frac{cos(x)}{x}-\frac{sin(x)}{x},x\ne 0 \end{array}\right. f(x)={1,x=0xsin(x),x=0f(x)={0,x=0xcos(x)−xsin(x),x=0
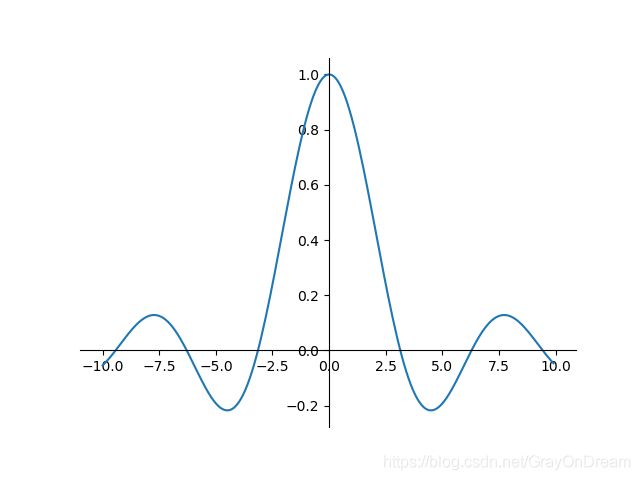
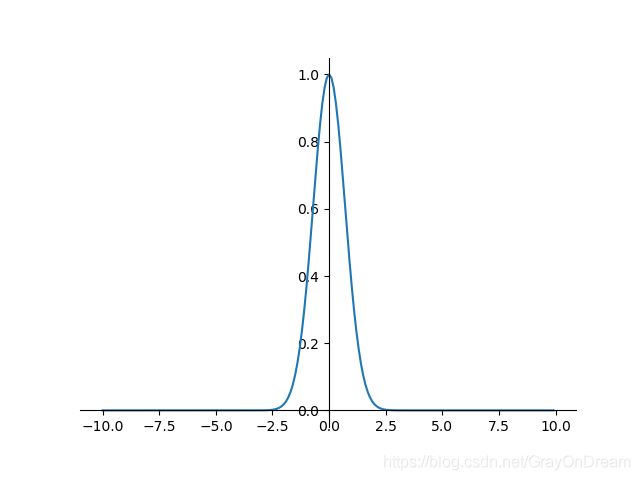
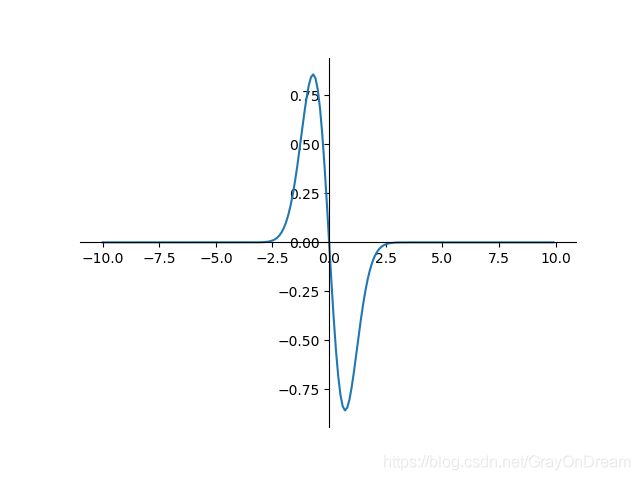
23、高斯函数
f ( x ) = e − x 2 f ′ ( x ) = − 2 x e − x 2 f(x)=e^{-x^2} \qquad\qquad f^{'}(x)=-2xe^{-x^2} f(x)=e−x2f′(x)=−2xe−x2