激活函数(ReLU, Swish, Maxout)
目录
1.ReLU(Rectified Linear Unit,修正线性单元)
ReLU 缺点
2.ReLU变种
Leaky ReLU
指数线性单元ELU
SELU
3.Swish
4.Maxout
Maxout激活函数
5.sigmoid & tanh
sigmoid作激活函数的优缺点
为什么tanh相比sigmoid收敛更快:
6.silu
激活函数的作用
梯度消失与梯度爆炸
激活函数选择
参考
神经网络中使用激活函数来加入非线性因素,提高模型的表达能力。
1.ReLU(Rectified Linear Unit,修正线性单元)
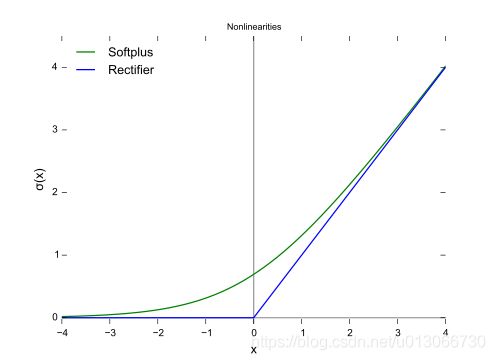
softplus函数与ReLU函数接近,但比较平滑, 同ReLU一样是单边抑制,有宽广的接受域(0,+inf), 但是由于指数运算,对数运算计算量大的原因,而不太被人使用.并且从一些人的使用经验来看(Glorot et al.(2011a)),效果也并不比ReLU好.
softplus的导数恰好是sigmoid函数.softplus 函数图像:
http://www.cs.utoronto.ca/~kriz/conv-cifar10-aug2010.pdf
ReLU的稀疏性(摘自这里):
当前,深度学习一个明确的目标是从数据变量中解离出关键因子。原始数据(以自然数据为主)中通常缠绕着高度密集的特征。然而,如果能够解开特征间缠绕的复杂关系,转换为稀疏特征,那么特征就有了鲁棒性(去掉了无关的噪声)。稀疏特征并不需要网络具有很强的处理线性不可分机制。那么在深度网络中,对非线性的依赖程度就可以缩一缩。一旦神经元与神经元之间改为线性激活,网络的非线性部分仅仅来自于神经元部分选择性激活。
对比大脑工作的95%稀疏性来看,现有的计算神经网络和生物神经网络还是有很大差距的。庆幸的是,ReLu只有负值才会被稀疏掉,即引入的稀疏性是可以训练调节的,是动态变化的。只要进行梯度训练,网络可以向误差减少的方向,自动调控稀疏比率,保证激活链上存在着合理数量的非零值。
ReLU 缺点
- 坏死: ReLU 强制的稀疏处理会减少模型的有效容量(即特征屏蔽太多,导致模型无法学习到有效特征)。由于ReLU在x < 0时梯度为0,这样就导致负的梯度在这个ReLU被置零,而且这个神经元有可能再也不会被任何数据激活,称为神经元“坏死”。
- 无负值: ReLU和sigmoid的一个相同点是结果是正值,没有负值.
2.ReLU变种
Leaky ReLU
指数线性单元ELU
SELU
self-Normalizing Neural Networks:https://arxiv.org/abs/1706.02515
对这篇论文的讨论:如何评价 Self-Normalizing Neural Networks 这篇论文? - 知乎
3.Swish
Searching for Activation functions:https://arxiv.org/abs/1710.05941
导数:
工程实现:
在TensorFlow框架中只需一行代码: x * tf.sigmoid(beta * x)或tf.nn.swish(x).
在Caffe中使用Scale+Sigmoid+EltWise(PROD)来实现或者合并成一个层.代码参考.
4.Maxout
论文Maxout Networks(Goodfellow,ICML2013)
假设网络第i层有2个神经元x1、x2,第i+1层的神经元个数为1个.原本只有一层参数,将ReLU或sigmoid等激活函数替换掉,引入Maxout,将变成两层参数,参数个数增为k倍.
优点:
- Maxout的拟合能力非常强,可以拟合任意的凸函数。
- Maxout具有ReLU的所有优点,线性、不饱和性。
- 同时没有ReLU的一些缺点。如:神经元的死亡。
缺点:
从上面的激活函数公式中可以看出,每个神经元中有两组(w,b)参数,那么参数量就增加了一倍,这就导致了整体参数的数量激增。
Maxout激活函数
与常规激活函数不同的是,它是一个可学习的分段线性函数.
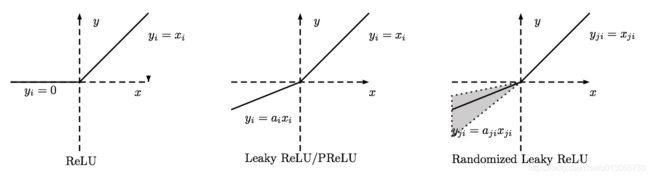
然而任何一个凸函数,都可以由线性分段函数进行逼近近似。其实我们可以把以前所学到的激活函数:ReLU、abs激活函数,看成是分成两段的线性函数,如下示意图所示:
5.sigmoid & tanh
hard tanh 限界: g(z) = max(-1, min(1,z))
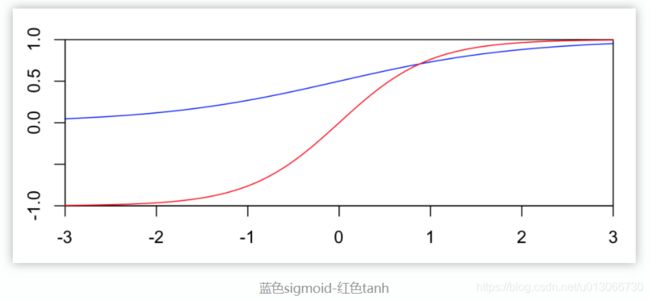
sigmoid & tanh 函数图像如下:
sigmoid作激活函数的优缺点
历史上很流行(Historically popular since they have nice interpretation as a saturating “firing rate” of a neuron),梯度计算较为方便:
优势是能够控制数值的幅度,在深层网络中可以保持数据幅度不会出现大的变化;而ReLU不会对数据的幅度做约束.
存在三个问题:
- 饱和的神经元会"杀死"梯度,指离中心点较远的x处的导数接近于0,停止反向传播的学习过程.
- sigmoid的输出不是以0为中心,而是0.5,这样在求权重w的梯度时,梯度总是正或负的.
- 指数计算耗时
为什么tanh相比sigmoid收敛更快:
6.silu
silu (x)=x∗ sigmoid(x)
激活函数的作用
梯度消失与梯度爆炸
梯度消失/爆炸原因及解决办法
原因,浅层的梯度计算需要后面各层的权重及激活函数导数的乘积,因此可能出现前层比后层的学习率小(vanishing gradient)或大(exploding)的问题,所以具有不稳定性.那么如何解决呢?
需要考虑几个方面:
- 权重初始化
使用合适的方式初始化权重, 如ReLU使用MSRA的初始化方式, tanh使用xavier初始化方式. - 激活函数选择
激活函数要选择ReLU等梯度累乘稳定的. - 学习率
一种训练优化方式是对输入做白化操作(包括正规化和去相关), 目的是可以选择更大的学习率. 现代深度学习网络中常使用Batch Normalization(包括正规化步骤,但不含去相关). (All you need is a good init. If you can't find the good init, use Batch Normalization.)
由于梯度的公式包含每层激励的导数以及权重的乘积,因此让中间层的乘积约等于1即可.但是sigmoid这种函数的导数值又与权重有关系(最大值1/4,两边对称下降),所以含有sigmoid的神经网络不容易解决,输出层的activation大部分饱和,因此不建议使用sigmoid.
ReLU在自变量大于0时导数为1,小于0时导数为0,因此可以解决上述问题.
梯度爆炸
由于sigmoid,ReLU等函数的梯度都在[0,1]以内,所以不会引发梯度爆炸问题。 而梯度爆炸需要采用梯度裁剪、BN、设置较小学习率等方式解决。
激活函数选择
- 首先尝试ReLU,速度快,但要注意训练的状态.
- 如果ReLU效果欠佳,尝试Leaky ReLU或Maxout等变种。
- 尝试tanh正切函数(以零点为中心,零点处梯度为1)
- sigmoid/tanh在RNN(LSTM、注意力机制等)结构中有所应用,作为门控或者概率值.
- 在浅层神经网络中,如不超过4层的,可选择使用多种激励函数,没有太大的影响。
参考
-
https://en.wikipedia.org/wiki/Rectifier_(neural_networks)↩
-
https://zh.wikipedia.org/wiki/%E5%8F%8C%E6%9B%B2%E5%87%BD%E6%95%B0↩
-
http://mathforum.org/library/drmath/view/54179.html↩
-
谈谈激活函数以零为中心的问题 https://liam0205.me/2018/04/17/zero-centered-active-function/↩
原文: https://www.cnblogs.com/makefile/p/activation-function.html © 康行天下