【菜菜的sklearn课堂笔记】逻辑回归与评分卡-梯度下降求解逻辑回归
视频作者:菜菜TsaiTsai
链接:【技术干货】菜菜的机器学习sklearn【全85集】Python进阶_哔哩哔哩_bilibili
我们以最著名也最常用的梯度下降法为例。
现在有一个带两个特征并且没有截距的逻辑回归 y ( x 1 , x 2 ) y(x_{1},x_{2}) y(x1,x2),两个特征所对应的参数分别为 [ θ 1 , θ 2 ] [\theta_{1},\theta_{2}] [θ1,θ2]。下面这个华丽的平面就是我们的损失函数 J ( θ 1 , θ 2 ) J(\theta_{1},\theta_{2}) J(θ1,θ2)在以 θ 1 , θ 2 , J \theta_{1},\theta_{2},J θ1,θ2,J为坐标轴的三维立体坐标系上的图像。现在,我们寻求的是损失函数的最小值,也就是图像的最低点。
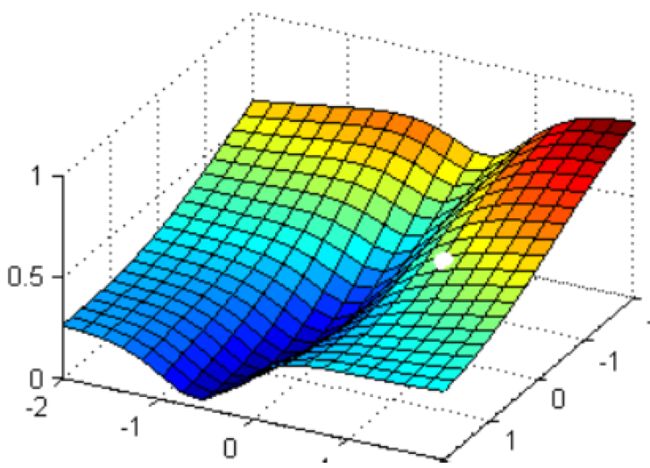
那我们怎么做呢?我在这个图像上随机放一个小球,当我松手,这个小球就会顺着这个华丽的平面滚落,直到滚到深蓝色的区域——损失函数的最低点。为了严格监控这个小球的行为,我让小球每次滚动的距离有限,不让他一次性滚到最低点,并且最多只允许它滚动100步,还要记下它每次滚动的方向,直到它滚到图像上的最低点。
这里的多次滚动可以这样理解
假设从释放位置到最低点有100的路程,我们第一次只允许小球走1,到位置一;从位置一开始,第二次只允许小球走1.2,到位置二(这里1,1.2是根据数据算出来的,是否相同不一定),这样小球需要很多次才能到达最低点
可以看见,小球从高处滑落,在深蓝色的区域中来回震荡,最终停留在了图像凹陷处的某个点上。非常明显,我们可以观察到几个现象:
- 首先,小球并不是一开始就直向着最低点去的,它先一口气冲到了蓝色区域边缘,后来又折回来,我们已经规定了小球是多次滚动,所以可见,小球每次滚动的方向都是不同的。
- 另外,小球在进入深蓝色区域后,并没有直接找到某个点,而是在深蓝色区域中来回震荡了数次才停下。这有两种可能:小球已经滚到了图像的最低点,所以停下了;由于设定的步数限制,小球还没有找到最低点,但也只好在100步的时候停下了(前面一节的Warning中有说到迭代次数不足就是这里的步数不够)。也就是说,小球不一定滚到了图像的最低处。
但无论如何,小球停下的就是我们在现有状况下可以获得的唯一点了。如果我们够幸运,这个点就是图像的最低点,那我们只要找到这个点的对应坐标 ( θ 1 ∗ , θ 2 ∗ , J min ) (\theta_{1}^{*},\theta_{2}^{*},J_{\min }) (θ1∗,θ2∗,Jmin),就可以获取能够让损失函数最小的参数取值 [ θ 1 ∗ , θ 2 ∗ ] [\theta_{1}^{*},\theta_{2}^{*}] [θ1∗,θ2∗]了。如此,梯度下降的过程就已经完成。
在这个过程中,小球其实就是一组组的坐标点 ( θ 1 , θ 2 , J ) (\theta_{1},\theta_{2},J) (θ1,θ2,J),小球每次滚动的方向就是那一个坐标点的梯度向量的反方向。因为每滚动一步,小球所在的位置都发生变化,坐标点和坐标点对应的梯度向量都发生了变化,所以每次滚动的方向也都不一样。人为设置的100次滚动限制,就是sklearn中逻辑回归的参数max_iter,代表着能走的最大步数,即最大迭代次数。
梯度下降推导
梯度:在多元函数上对各个自变量求偏导数,把求得的各个自变量的偏导数以向量的形式写出来,就是梯度。
梯度是一个向量,因此它有大小也有方向。它的大小,就是偏导数组成的向量模长,记作 d d d。它的方向,几何上来说,就是损失函数 J ( θ ) J(\theta) J(θ)的值增加最快的方向,就是小球每次滚动的方向的反方向。
根据概念,首先我们要明确,我们要求的梯度是损失函数 J ( θ 1 , θ 2 ) J(\theta_{1},\theta_{2}) J(θ1,θ2)的梯度,也就是 J ( θ 1 , θ 2 ) J(\theta_{1},\theta_{2}) J(θ1,θ2)对 θ 1 , θ 2 \theta_{1},\theta_{2} θ1,θ2的偏导
核心误区:到底在哪个函数上,求什么的偏导数?
注意,在一些博客或教材中,讲解梯度向量的定义时会写一些让人容易误解的句子,比如“对多元函数的参数求偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度”。注意,这种解释是不太严谨的。
一个多元函数的梯度,是对其自变量求偏导的结果,不是对其参数求偏导的结果。但是在逻辑回归的数学过程中,损失函数 J ( θ ) J(\theta) J(θ)的自变量刚好是逻辑回归的预测函数 y ( x ) y(x) y(x)的参数,所以才造成了这种让人误解的。因此,求解梯度的方式,和逻辑回归本身的预测函数 y ( x ) y(x) y(x)没有一丝联系。
强调:求解梯度,是在损失函数 J ( θ ) J(\theta) J(θ)上对损失函数自身的自变量 θ i \theta_{i} θi求解偏导,而这个自变量,刚好是逻辑回归预测函数 y ( x ) = 1 1 + e − θ x \begin{aligned} y(x)=\frac{1}{1+e^{-\theta x}}\end{aligned} y(x)=1+e−θx1的参数
之前我们知道,损失函数是
J ( θ ) = − ∑ i = 1 n [ y i log y θ ( x i ) + ( 1 − y i ) log ( 1 − y θ ( x i ) ) ] J(\theta)=-\sum\limits_{i=1}^{n}[y_{i}\log y_{\theta}(x_{i})+(1-y_{i})\log (1-y_{\theta}(x_{i}))] J(θ)=−i=1∑n[yilogyθ(xi)+(1−yi)log(1−yθ(xi))]
利用梯度下降求最小值
∂ J ( θ ) ∂ θ j = − ∑ i = 1 n [ y i ⋅ 1 y θ ( x i ) ⋅ ∂ y θ ( x i ) ∂ θ j + ( 1 − y i ) ⋅ 1 1 − y θ ( x i ) ⋅ ( − ∂ y θ ( x i ) ∂ θ j ) ] = − ∑ i = 1 n [ y i ⋅ 1 y θ ( x i ) − ( 1 − y i ) ⋅ 1 1 − y θ ( x i ) ] ⋅ ∂ y θ ( x i ) ∂ θ j = − ∑ i = 1 n [ y i ⋅ 1 y θ ( x i ) − ( 1 − y i ) ⋅ 1 1 − y θ ( x i ) ] ⋅ y θ ( x i ) ( 1 − y θ ( x i ) ) ⋅ x i j = − ∑ i = 1 n [ y i ⋅ ( 1 − y θ ( x i ) ) − ( 1 − y i ) ⋅ y θ ( x i ) ] ⋅ x i j = − ∑ i = 1 n [ y i ⋅ − y θ ( x i ) ] ⋅ x i j = ∑ i = 1 n [ y θ ( x i ) − y i ] ⋅ x i j \begin{aligned} \frac{\partial J(\theta)}{\partial \theta_{j}}&=- \sum\limits_{i=1}^{n}\left[y_{i} \cdot \frac{1}{y_{\theta}(x_{i})}\cdot \frac{\partial y_{\theta}(x_{i})}{\partial \theta_{j}}+(1-y_{i})\cdot \frac{1}{1-y_{\theta}(x_{i})}\cdot \left(- \frac{\partial y_{\theta}(x_{i})}{\partial \theta_{j}}\right)\right]\\ &=-\sum\limits_{i=1}^{n}\left[y_{i} \cdot \frac{1}{y_\theta(x_{i})}-(1-y_{i})\cdot \frac{1}{1-y_{\theta}(x_{i})}\right]\cdot \frac{\partial y_{\theta}(x_{i})}{\partial \theta_{j}}\\ &=-\sum\limits_{i=1}^{n}\left[y_{i} \cdot \frac{1}{y_\theta(x_{i})}-(1-y_{i})\cdot \frac{1}{1-y_{\theta}(x_{i})}\right]\cdot y_{\theta}(x_{i})(1-y_{\theta}(x_{i}))\cdot x_{ij}\\ &=-\sum\limits_{i=1}^{n}[y_{i} \cdot (1-y_{\theta}(x_{i}))-(1-y_{i})\cdot y_{\theta}(x_{i})]\cdot x_{ij}\\ &=-\sum\limits_{i=1}^{n}[y_{i} \cdot -y_{\theta}(x_{i})]\cdot x_{ij}\\ &=\sum\limits_{i=1}^{n}[y_{\theta}(x_{i})-y_{i}]\cdot x_{ij} \end{aligned} ∂θj∂J(θ)=−i=1∑n[yi⋅yθ(xi)1⋅∂θj∂yθ(xi)+(1−yi)⋅1−yθ(xi)1⋅(−∂θj∂yθ(xi))]=−i=1∑n[yi⋅yθ(xi)1−(1−yi)⋅1−yθ(xi)1]⋅∂θj∂yθ(xi)=−i=1∑n[yi⋅yθ(xi)1−(1−yi)⋅1−yθ(xi)1]⋅yθ(xi)(1−yθ(xi))⋅xij=−i=1∑n[yi⋅(1−yθ(xi))−(1−yi)⋅yθ(xi)]⋅xij=−i=1∑n[yi⋅−yθ(xi)]⋅xij=i=1∑n[yθ(xi)−yi]⋅xij
其中
∂ y θ ( x i ) ∂ θ j = ( 1 1 + e − θ T x i ) ′ = 1 ′ ⋅ ( 1 + e − θ T x i ) − 1 ⋅ e − θ T x i ⋅ ( − θ T x i ) ′ ( 1 + e − θ T x i ) 2 注 意 从 这 往 上 是 x i , 往 下 是 x i j = x i j e − θ T x i ( 1 + e − θ T x i ) 2 = 1 1 + e − θ T x i ⋅ e − θ T x i 1 + e − θ T x i ⋅ x i j = y θ ( x i ) ( 1 − y θ ( x i ) ) ⋅ x i j \begin{aligned} \frac{\partial y_{\theta}(x_{i})}{\partial \theta_{j}}&=\left(\frac{1}{1+ e^{-\theta^{T}x_{i}}}\right)'\\ &=\frac{1' \cdot (1+e^{-\theta^{T}x_{i}})-1 \cdot e^{-\theta^{T}x_{i}}\cdot (-\theta^{T}x_{i})'}{(1+e^{-\theta^{T}x_{i}})^{2}}\\ &注意从这往上是x_{i},往下是x_{ij}\\ &=\frac{x_{ij}e^{-\theta^{T}x_{i}}}{(1+e^{-\theta^{T}x_{i}})^{2}}\\ &=\frac{1}{1+e^{-\theta^{T}x_{i}}}\cdot \frac{e^{-\theta^{T}x_{i}}}{1+e^{-\theta^{T}x_{i}}}\cdot x_{ij}\\ &=y_{\theta}(x_{i})(1-y_{\theta}(x_{i}))\cdot x_{ij} \end{aligned} ∂θj∂yθ(xi)=(1+e−θTxi1)′=(1+e−θTxi)21′⋅(1+e−θTxi)−1⋅e−θTxi⋅(−θTxi)′注意从这往上是xi,往下是xij=(1+e−θTxi)2xije−θTxi=1+e−θTxi1⋅1+e−θTxie−θTxi⋅xij=yθ(xi)(1−yθ(xi))⋅xij参考链接:逻辑回归梯度下降法_matao_jack的博客-CSDN博客_逻辑回归梯度下降
对损失函数的自变量 θ \theta θ求导,就可以得到梯度向量在第 j j j组 θ \theta θ的坐标点上的表示形式
∂ J ( θ ) ∂ θ j = ∑ i = 1 n [ y θ ( x i ) − y i ] ⋅ x i j \frac{\partial J(\theta)}{\partial \theta_{j}}=\sum\limits_{i=1}^{n}[y_{\theta}(x_{i})-y_{i}]\cdot x_{ij} ∂θj∂J(θ)=i=1∑n[yθ(xi)−yi]⋅xij
在这个公式下,只要给定一组取值 θ \theta θ,其中第 j j j个维度的取值为 θ j \theta_{j} θj,再代入特征矩阵 X X X,就可以求得这一组 θ \theta θ取值下的预测结果 y θ ( x i ) y_{\theta}(x_{i}) yθ(xi),结合真实标签向量 y y y,就可以获得 θ j \theta_{j} θj对应维度下的梯度向量,其大小表示为 d j d_{j} dj
之前说过,我们的目的是在 θ \theta θ可能的取值上进行遍历,一次次计算梯度向量,并在梯度向量的反方向上让损失函数 J J J下降至最小值。在这个过程中,我们的 θ \theta θ和梯度向量的大小 d d d都会不断改变,而我们迭代 θ \theta θ的过程可以描述为:
θ j m + 1 = θ j m − α ⋅ d j = θ j m − α ∑ i = 1 n [ y θ ( x i ) − y i ] ⋅ x i j \theta_{j}^{m+1}=\theta_{j}^{m}- \alpha \cdot d_{j}=\theta_{j}^{m}- \alpha \sum\limits_{i=1}^{n}[y_{\theta}(x_{i})-y_{i}]\cdot x_{ij} θjm+1=θjm−α⋅dj=θjm−αi=1∑n[yθ(xi)−yi]⋅xij
其中 θ j m + 1 \theta_{j}^{m+1} θjm+1是第 m m m次迭代后的参数向量, θ j m \theta_{j}^{m} θjm是 m m m次迭代的参数向量, α \alpha α被称为步长,控制着每走一步(每迭代一次)后 θ \theta θ的变化,并以此来影响迭代后的梯度向量的大小和方向, d j d_{j} dj是 j j j维度上在该点处梯度向量的长度
步长的理解误区
核心误区:步长到底是什么?
许多博客和教材在描述步长的时候,称它是”梯度下降中每一步沿梯度的反方向前进的长度“,”沿着最陡峭最易下山的位置走的那一步的长度“或者”梯度下降中每一步损失函数减小的量“,甚至有说,步长是二维平面著名的求导三角形中的”斜边“或者“对边”的。
这些说法都是错误的!
来看下面这一张二维平面的求导三角型图。类比到我们的损失函数和梯度概念上,图中的抛物线就是我们的损失函数 J ( θ ) J(\theta) J(θ), A ( θ a , J ( θ a ) ) A(\theta_{a},J(\theta_{a})) A(θa,J(θa))就是小球最初在的位置, B ( θ b , J ( θ b ) ) B(\theta_{b},J(\theta_{b})) B(θb,J(θb))就是一次滚动后小球移动到的位置。从 A A A到 B B B的方向就是梯度向量的反方向,指向损失函数在 A A A点下降最快的方向。而梯度向量的大小是点 A A A在图像上对 θ \theta θ求导后的结果,也是点 A A A切线方向的斜率,橙色角的 tan \tan tan结果,记作 d d d。

梯度下降每走一步,损失函数减少的量,是损失函数在 θ \theta θ变化之后的取值的变化,写作 J ( θ b ) − J ( θ a ) J(\theta_{b})-J(\theta_{a}) J(θb)−J(θa),这是二维平面求导三角形中的对边
梯度下降每走一步,参数向量的变化,写作 θ b − θ a \theta_{b}-\theta_{a} θb−θa,根据我们参数向量的迭代公式 θ j m + 1 = θ j m − α ⋅ d j \begin{aligned} \theta_{j}^{m+1}=\theta_{j}^{m}- \alpha \cdot d_{j}\end{aligned} θjm+1=θjm−α⋅dj,也就有 θ b − θ a = α ⋅ d \theta_{b}-\theta_{a}=\alpha \cdot d θb−θa=α⋅d
梯度下降中每走一步,下降的距离,是 ( α ⋅ d ) 2 + ( J ( θ a ) − J ( θ b ) ) 2 \sqrt{(\alpha \cdot d)^{2}+(J(\theta_{a})-J(\theta_{b}))^{2}} (α⋅d)2+(J(θa)−J(θb))2,是对边和邻边的根号下平方和,是二维平面的求导三角型中的”斜边“。
所以,步长不是任何物理距离,它甚至不是梯度下降过程中任何距离的直接变化,它是梯度向量的大小 上的一个比例,影响着参数向量 每次迭代后改变的部分。