光流估计方法

光流估计方法

1. 光流计算中的恒定亮度假设

光流的概念是Gibson在1950年首先提出来的。它是空间运动物体在观察成像平面上的像素运动的瞬时速度，是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系，从而计算出相邻帧之间物体的运动信息的一种方法。一般而言，光流是由于场景中前景目标本身的移动、相机的运动，或者两者的共同运动所产生的。

2.假设条件

（1）亮度恒定，就是同一点随着时间的变化，其亮度不会发生改变。这是基本光流法的假定（所有光流法变种都必须满足），用于得到光流法基本方程；

（2）小运动，这个也必须满足，就是时间的变化不会引起位置的剧烈变化，这样灰度才能对位置求偏导（换句话说，小运动情况下我们才能用前后帧之间单位位置变化引起的灰度变化去近似灰度对位置的偏导数），这也是光流法不可或缺的假定；

（3）空间一致，一个场景上邻近的点投影到图像上也是邻近点，且邻近点速度一致。这是Lucas-Kanade光流法特有的假定，因为光流法基本方程约束只有一个，而要求x，y方向的速度，有两个未知变量。我们假定特征点邻域内做相似运动，就可以连立n多个方程求取x，y方向的速度（n为特征点邻域总点数，包括该特征点）。

研究光流场的目的就是为了从图片序列中近似得到不能直接得到的运动场。运动场，其实就是物体在三维真实世界中的运动在图像上的二位速度矢量投影；光流场，是三维物体的运动在二维图像平面上（人的眼睛或者摄像头）亮度模式的投影。

那通俗的讲就是通过一个图片序列，把每张图像中每个像素的运动速度和运动方向找出来就是光流场。那怎么找呢？咱们直观理解肯定是：第t帧的时候A点的位置是(x1, y1)，那么我们在第t+1帧的时候再找到A点，假如它的位置是(x2,y2)，那么我们就可以确定A点的运动了：(ux, vy) = (x2, y2) - (x1,y1)。

那怎么知道第t+1帧的时候A点的位置呢？ 这就存在很多的光流计算方法了。

1981年，Horn和Schunck创造性地将二维速度场与灰度相联系，引入光流约束方程，得到光流计算的基本算法。人们基于不同的理论基础提出各种光流计算方法，算法性能各有不同。Barron等人对多种光流计算技术进行了总结，按照理论基础与数学方法的区别把它们分成四种：基于梯度的方法、基于匹配的方法、基于能量的方法、基于相位的方法。近年来神经动力学方法也颇受学者重视。

3. L-K光流估计方法的基本原理:

L-K光流估计方法属于一种基于匹配的光流计算方法，其包括基于特征和区域的两种。基于特征的方法不断地对目标主要特征进行定位和跟踪，对目标大的运动和亮度变化具有鲁棒性（robustness）。存在的问题是光流通常很稀疏，而且特征提取和精确匹配也十分困难。基于区域的方法先对类似的区域进行定位，然后通过相似区域的位移计算光流。这种方法在视频编码中得到了广泛的应用。然而，它计算的光流仍不稠密。另外，这两种方法估计亚像素精度的光流也有困难，计算量很大。在考虑光流精度和稠密性时，基于匹配的方法适用。

根据上面的光流估计基本模型得出方程IxΔx+IyΔy=−It，任务:求(u,v)=(Δx,Δy)

困难:一个方程包含两个未知数。

Lucas-Kanade方法采用基于领域的计算方法，假设在一个小方格里的所有像素位移相同。则会得到一组光流估计方程。用矩阵表示如下:


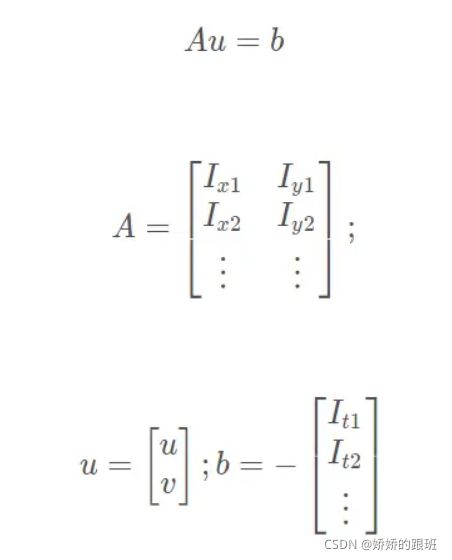
类似前述求解，可得

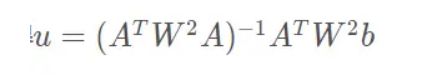
可信度判断:矩阵求逆是否能实现？

我们在计算光流的时候，我们要求图像对应位置灰度变化充分(具有充分特征)，假如位置灰度变化平缓，那么沿x和y方向的偏倒就可能为0，那么上述式子不可求逆，也就无法计算光流。

通过特征值判断是否计算可信 在数学上我们要判断矩阵是否可逆，我们可以通过计算特征值来判断。如果两个特征值远大于0，那么矩阵求逆是可靠的。假如有一个特征值接近于0的话，那么矩阵求逆是不可靠的。

4.代码实现

import numpy as np
import cv2


#cap = cv2.VideoCapture(0)#摄像头
cap = cv2.VideoCapture('D:\jupyter\img/vtest.avi') #视频

# ShiTomasi 角点检测参数
feature_params = dict( maxCorners = 100,
                       qualityLevel = 0.3,
                       minDistance = 7,
                       blockSize = 7 )

# lucas kanade光流法参数
lk_params = dict( winSize  = (15,15),
                  maxLevel = 2,
                  criteria = (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 0.03))

# 创建随机颜色
color = np.random.randint(0,255,(100,3))

# 获取第一帧，找到角点
ret, old_frame = cap.read()
#找到原始灰度图
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)

#获取图像中的角点，返回到p0中
p0 = cv2.goodFeaturesToTrack(old_gray, mask = None, **feature_params)

# 创建一个蒙版用来画轨迹
mask = np.zeros_like(old_frame)

while(1):
    ret,frame = cap.read()
    frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

    # 计算光流
    p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)
    # 选取好的跟踪点
    good_new = p1[st==1]
    good_old = p0[st==1]

    # 画出轨迹
    for i,(new,old) in enumerate(zip(good_new,good_old)):
        a,b = new.ravel()
        c,d = old.ravel()
        mask = cv2.line(mask,(int(a), int(b)), (int(c),int(d)), color[i].tolist(), 2)
        frame = cv2.circle(frame,(int(a),int(b)),5,color[i].tolist(),-1)
    img = cv2.add(frame,mask)

    cv2.imshow('frame',img)
    k = cv2.waitKey(30) & 0xff
    if k == 27:
        break

    # 更新上一帧的图像和追踪点
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1,1,2)

cv2.destroyAllWindows()
cap.release()

5. 实现效果图