处理多维特征&数据集的加载

参考视频：08.加载数据集_哔哩哔哩_bilibili

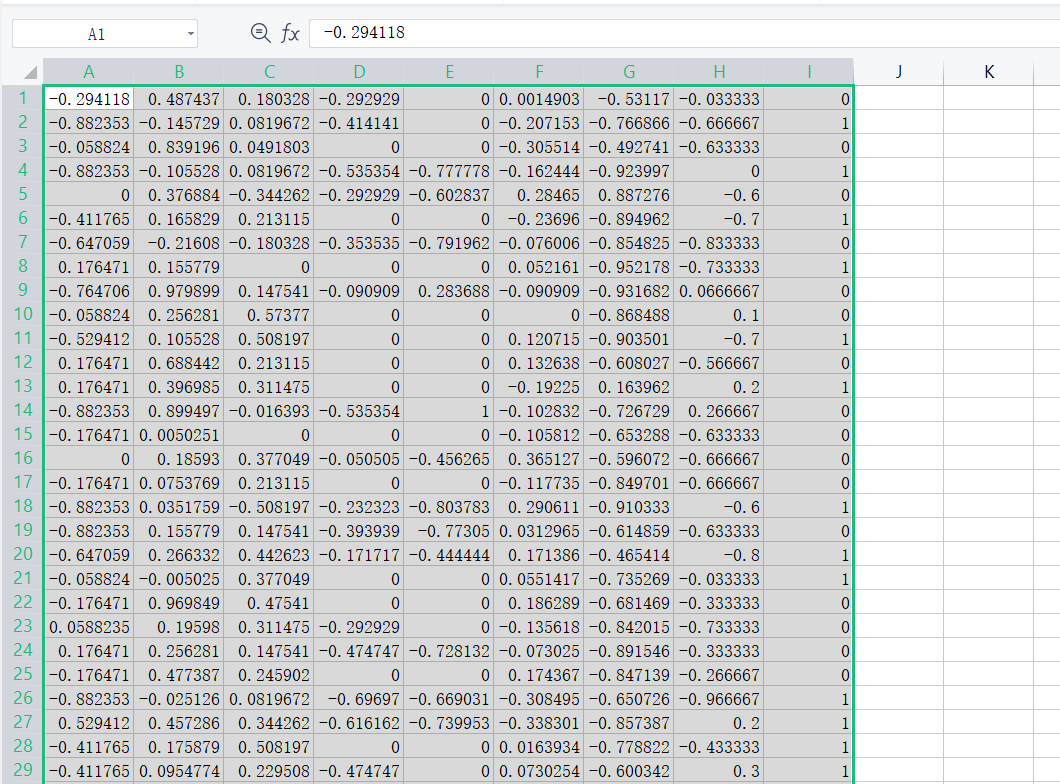
这里选择的数据集是糖尿病患者的数据集，一共有759条数据，通过8个指标对患者病情是否会加重进行判断（这里未对数据做预处理）

很显然，这是一个二分类的问题，在这个问题中，我们可以使用交叉熵来作为损失函数

$$loss=-\frac{1}{N}\sum _{n=1}^N(ylog\hat{y}+(1-y)log\hat{y})$$

1 对所有数据进行操作

一开始我的做法如下，一次性读入所有数据，学习率为0.1，训练100轮

并输出loss、准确率、召回率（相关概念参考准确率、精确率、召回率 - 知乎 (zhihu.com)、

(127条消息) pytorch损失函数中‘reduction‘参数_新嬉皮士的博客-CSDN博客）

import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)  # 读取数据，神经网络上通常使用float32
x_data = torch.from_numpy(xy[:, :-1])  # 取每一行除了最后一列的所有数据
y_data = torch.from_numpy(xy[:, [-1]])  # 取每一行最后一列的数据


class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 16)
        self.linear2 = torch.nn.Linear(16, 8)
        self.linear3 = torch.nn.Linear(8, 1)
        self.activate = nn.Sigmoid()

    def forward(self, x):
        x = self.activate(self.linear1(x))
        x = self.activate(self.linear2(x))  # 上一次的输入作为这一层的输出
        x = self.activate(self.linear3(x))  # 上一次的输入作为这一层的输出
        return x


model = Model()

criterion = nn.BCELoss(reduction='mean')  # 用交叉熵作为损失函数
optimizer = torch.optim.Adam(model.parameters(), lr=0.1)  # 设置优化器Adam，学习率0.1

loss_list = []
for epoch in range(100):
    # forward
    np.random.shuffle(xy)
    x_data = torch.from_numpy(xy[:, :-1])  # 取每一行除了最后一列的所有数据
    y_data = torch.from_numpy(xy[:, [-1]])  # 取每一行最后一列的数据
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    y_copy = y_pred.detach().numpy().copy()
    y_copy[y_copy < 0.5], y_copy[y_copy > 0.5] = 0, 1
    ret = np.sum(y_copy == y_data.detach().numpy())

    TP = np.sum((y_copy + y_data.detach().numpy()) == 2)    # TP（True Positive）：正确的正例，一个实例是正类并且也被判定成正类
    FN = np.sum((y_copy - y_data.detach().numpy()) == -1)   # FN（False Negative）：错误的反例，漏报，本为正类但判定为假类
    FP = np.sum((y_copy - y_data.detach().numpy()) == 1)    # FP（False Positive）：错误的正例，误报，本为假类但判定为正类
    TN = np.sum((y_copy + y_data.detach().numpy()) == 0)    # TN（True Negative）：正确的反例，一个实例是假类并且也被判定成假类
    print(epoch, ' ', loss.item(), ' ', ret/len(y_copy), ' ', TP/(TP+FN))   # 输出损失、准确率以及召回率

    # backward
    optimizer.zero_grad()
    loss.backward()

    # update
    optimizer.step()

    loss_list.append(loss.data)

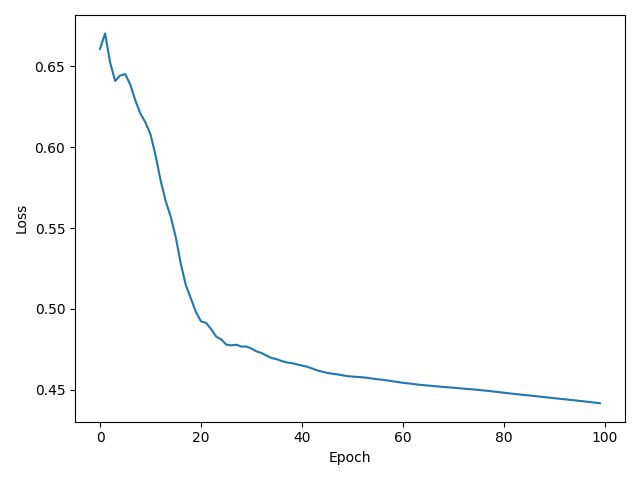
# 绘制Epoch-Loss曲线
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.plot(np.arange(0, 100, 1), np.array(loss_list))
plt.show()

结果如下：

2 加入mini-batch

需要从pytorch中引入这两个包

from torch.utils.data import Dataset
from torch.utils.data import DataLoader

同时要对Dataset抽象类进行继承并设计好我们需要的数据集类：

class DiabetesDataset(Dataset):
    def __init__(self):
        pass

    def __getitem__(self, index):  # 使得能够支持下标操作
        pass

    def __len__(self):  # 能够进行条数的反馈
        pass
    
dataset = DiabetesDataset()

对数据进行加载使用DataLoader（数据集，batch大小，是否打乱，多线程读取）

train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=0)

完整代码如下：

import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
import numpy as np
import matplotlib.pyplot as plt

# 1.准备数据集
class DiabetesDataset(Dataset):
    def __init__(self, filepath):
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)  # 读取数据，神经网络上通常使用float32
        self.len = xy.shape[0]  # 获取到数据的总条数（即行）
        self.x_data = torch.from_numpy(xy[:, :-1])  # 取每一行除了最后一列的所有数据
        self.y_data = torch.from_numpy(xy[:, [-1]])  # 取每一行最后一列的数据

    def __getitem__(self, index):  # 使得能够支持下标操作
        return self.x_data[index], self.y_data[index]  # 返回一个元组

    def __len__(self):  # 能够进行条数的反馈
        return self.len

dataset = DiabetesDataset('diabetes.csv.gz')
# 传递数据集，设置batch大小，是否打乱，多线程（Windows下最好设置为0）
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=0)

# 2.构造模型
class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 16)
        self.linear2 = torch.nn.Linear(16, 8)
        self.linear3 = torch.nn.Linear(8, 1)
        self.activate = nn.Sigmoid()

    def forward(self, x):
        x = self.activate(self.linear1(x))
        x = self.activate(self.linear2(x))  # 上一次的输入作为这一层的输出
        x = self.activate(self.linear3(x))  # 上一次的输入作为这一层的输出
        return x


model = Model()

# 3.构造损失和优化器
criterion = nn.BCELoss(reduction='mean')  # 用交叉熵作为损失函数
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)  # 设置优化器Adam，学习率0.01


# 4.训练
loss_list = []
for epoch in range(100):
    # 等价于 for i,(inputs,labels) in enumerate(train_loader,0)
    loss_epoch = 0
    for i, data in enumerate(train_loader, 0):  # i表示当前迭代次数，0表示从1开始
        inputs, labels = data
        y_pred = model(inputs)
        loss = criterion(y_pred, labels)
        loss_epoch += loss.data
        print(epoch, i, loss.item())

    loss_list.append(loss_epoch / 24)
    # backward
    optimizer.zero_grad()
    loss.backward()

    # update
    optimizer.step()


# 绘制Epoch-Loss曲线
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.plot(np.arange(0, 100, 1), np.array(loss_list))
plt.show()

这次只输出loss，loss在0.4-0.6之间波动

3 总结

加入mini-batch后观察代码，主要分为4个步骤：

1. Prepare dataset：准备数据集
2. Design model using Class：构造模型
3. Construct loss and optimizer：构造损失和优化器
4. Training cycle：训练